ПАРАЛЛЕЛИ И МЕРИДИАНЫ

В IV в. до н. э. величайший мыслитель древности Аристотель доказал, что наша планета имеет форму, очень близкую к форме шара.

Примерно в то же время, наблюдая во время путешествий в различных местах видимое движение звезд и Солнца, древние ученые установили для ориентировки на земной поверхности определенные условные линии.

Отправимся в мысленное путешествие по поверхности Земли. Положение над горизонтом воображаемой оси мира, вокруг которой происходит суточное вращение небесного свода, будет для нас все время меняться. В соответствии с этим будет меняться и картина движения звездного неба.

Поехав на север, мы увидим, что звезды в южной части неба поднимаются каждую ночь на меньшую высоту. А звезды в северной части - в нижней кульминации - имеют большую высоту. Двигаясь достаточно долго, мы попадем на Северный полюс. Здесь вообще ни одна звезда не поднимается и не опускается. Нам будет казаться, что все небо медленно кружится параллельно горизонту.

Древние путешественники не знали, что видимое движение звезд является отражением вращения Земли. И они не бывали на полюсе. Но им необходимо было иметь ориентир на земной поверхности. И они выбрали для этой цели легко определяемую по звездам линию север - юг. Эта линия получила название меридиана.

Меридианы можно проводить через любые точки на поверхности Земли. Множество меридианов образует систему воображаемых линий, соединяющих Северный и Южный полюсы Земли, которые удобно использовать для определения местоположения.

Примем один из меридианов на начальный. Положение любого другого меридиана в этом случае будет известно, если указано направление отсчета и задан двугранный угол между искомым меридианом и начальным.

В настоящее время по международному соглашению условились считать начальным тот меридиан, который проходит через одну из старейших в мире астрономических обсерваторий - Гринвичскую обсерваторию, расположенную на окраине Лондона. Угол, образованный каким-либо меридианом с начальным, называют долготой. Долгота, например, меридиана Москвы 37° к востоку от Гринвича.

Чтобы отличить друг от друга точки, лежащие на одном и том же меридиане, пришлось ввести вторую географическую координату - широту. Широтой называют угол, который проведенная в данном месте поверхности Земли отвесная линия образует с плоскостью экватора.

Термины долгота и широта дошли до нас от древних мореходов, которые описывали длину и ширину Средиземного моря. Та координата, которая соответствовала измерениям длины Средиземного моря, стала долготой, а та, которая соответствовала ширине, стала современной широтой.

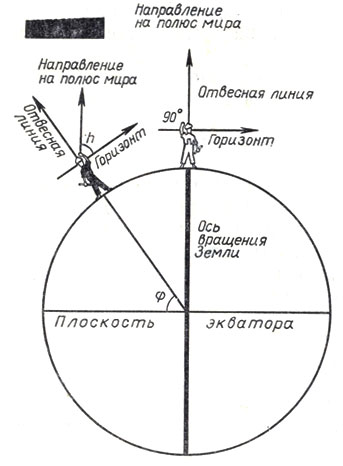
Высота полюса мира над горизонтом равна широте места наблюдений

Нахождение широты, как и определение направления меридиана, тесно связано с движением звезд. Уже древние астрономы доказали, что высота полюса мира над горизонтом в точности равна широте места.

Предположим, что Земля имеет форму правильного шара, и рассечем ее по одному из меридианов, как на рисунке. Пусть на Северном полюсе стоит человек, изображенный на рисунке в виде светлой фигуры. Для него направление вверх, т. е. направление отвесной линии, совпадает с осью мира. Полюс мира находится у него прямо над головой. Высота полюса мира равна здесь 90 .

Так как видимое вращение звезд вокруг оси мира является отражением реального вращения Земли, то в любой точке Земли, как мы уже знаем, направление оси мира остается параллельным направлению оси вращения Земли. Направление же отвесной линии при переходе из точки в точку меняется.

Возьмем, например, другого человека (на рисунке - темная фигура). Направление оси мира у него осталось таким же, как и у первого. А направление отвесной линии изменилось. Поэтому высота полюса мира над горизонтом здесь не 90°, а значительно меньше.

Из простых геометрических соображений ясно, что высота полюса мира над горизонтом (на рисунке угол ft) действительно равна широте (угол ф).

Линия, соединяющая точки с одинаковыми широтами, получила название параллели.

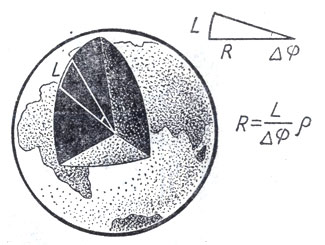
Принцип определения радиуса Земли. Коэффициент p в формуле служит для перехода от градусной меры к радианной

Меридианы и параллели образуют так называемую систему географических координат. Каждая точка на земной поверхности имеет вполне определенную долготу и широту. И наоборот, если известна широта и долгота, то можно построить одну параллель и один меридиан, в пересечении которых получится одна единственная точка.

Понимание особенностей суточного движения звезд и введение системы географических координат позволили осуществить первое определение радиуса Земли. Оно было выполнено во второй половине III в. до н. э. известным математиком и географом Эратосфеном.

Принцип этого определения заключается в следующем. Пусть удалось измерить разность широт двух точек, лежащих на одном меридиане (см. рис.). Тем самым нам стал известен угол Дф с вершиной в центре Земли, который соответствует дуге меридиана L на поверхности Земли. Если теперь удастся измерить также и дугу L, то мы получим сектор с известной длиной дуги и соответствующим ей центральным углом. На рисунке этот сектор показан отдельно. Путем несложных вычислений можно получить величину радиуса этого сектора, который и является радиусом Земли.

Наблюдения Эратосфена

Эратосфен, грек по национальности, жил в богатом египетском городе Александрии. К югу от Александрии находился другой город - Сиена, который в наши дни называется Асуаном и где, как известно, с помощью Советского Союза сооружена знаменитая высотная плотина. Эратосфен знал, что Сиена обладает интересной особенностью. В полдень одного из июньских дней Солнце над Сиеной бывает настолько высоко, что его отражение видно на дне даже очень глубоких колодцев. Отсюда Эратосфен заключил, что высота Солнца в Сиене в этот день равна точно 90°. Кроме того, раз Сиена лежит строго к югу от Александрии, то они находятся на одном меридиане.

Для необычного измерения Эратосфен решил воспользоваться скафисом - чашеобразными солнечными часами со штырьком и делениями внутри них. Установленные вертикально, эти солнечные часы по тени от штырька дают возможность измерить высоту Солнца над горизонтом. И в полдень того самого дня, когда Солнце над Сиеной поднялось настолько высоко, что все предметы перестали отбрасывать тени. Эратосфен измерил его высоту на городской площади Александрии. Высота Солнца в Александрии, по измерениям Эратосфена, оказалась равной 82° 48'. Стало быть, разность широт Александрии и Сиены составляет 90° 00' - 82° 48' = 7° 12'.

Оставалось измерить расстояние между ними. Но как это сделать? Как измерить на поверхности Земли расстояние, равное в современных единицах примерно 800 км?

Трудности подобного предприятия были тогда буквально неисчислимы.

Действительно, как изготовить такую гигантскую линейку, с помощью которой можно было бы произвести измерения? Как сделать, чтобы на протяжении 800 км эта линейка укладывалась строго по меридиану, без всяких перекосов?

Необходимые данные о расстоянии между городами пришлось взять из рассказов купцов, водивших торговые караваны из Александрии в Сиену. Купцы говорили, что расстояние между ними составляет примерно 5000 греческих стадиев. Эратосфен принял это значение за истинное и, использовав его, вычислил величину радиуса Земли.

Если сравнить полученную Эратосфеном величину с современными данными, то получится, что он ошибся относительно немного - всего только на 100 км.

Так, с III в. до н. э., со времени Эратосфена, переплелись пути астрономии и геодезии - другой древней науки, изучающей форму и размеры как всей Земли в целом, так и отдельных ее частей.

Методы астрономических определений широт развивались и совершенствовались. Это было особенно важно, в частности, именно в связи с необходимостью более тщательного определения размера Земли. Ибо, начиная с того же Эратосфена, было уяснено, что задача определения размера Земли распадается на две части: астрономическую, т. е. определение разности широт, и геодезическую, т. е. определение длины дуги меридиана. Эратосфен сумел решить астрономическую часть задачи, и принципиально тем же путем шли многочисленные его последователи.

Мы еще будем иметь случай рассказать о более точных измерениях размера Земли, а пока, освоившись с определением широт, займемся делом значительно более сложным - определением географических долгот.