ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ

В старости Ньютон заметил как-то, что если он и сумел добиться в науке важных результатов, то только потому, что стоят на плечах исполинов. В этих словах заключен великий смысл, и именно их мы вынесли в заголовок второй части нашей книги, посвященной истории идей и методов современной астрономии. Преемственность крупных научных открытий - их важнейшее и неотъемлемое свойство. Коперник, Кеплер, Галилей, Ньютон - это единая линия развития астрономической науки.

Ньютон широко известен своими работами в области механики и оптики, он первым разложил солнечный свет в спектр и разработал дифференциальное исчисление, далеко двинул вперед многие разделы математики и физики. И малой доли этих работ за глаза хватило бы, чтобы навеки прославить имя любого ученого. Но Ньютону принадлежит и еще одна заслуга, которая по сути дела затмила все остальные: он сформулировал закон всемирного тяготения.

Исаак Ньютон (1643-1727)

Всю свою жизнь Ньютон руководствовался знаменитым принципом: hypotesis nоn fingo - «гипотез не выдумываю». Этот-то принцип и нашел самое яркое воплощение в формулировке закона всемирного тяготения:

все тела притягиваются друг к другу с силой прямо пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.

Ньютон открыл закон, управляющий взаимодействием тел, без всякого рассмотрения природы или причин этого взаимодействия: он дал образец решения физической задачи математическими методами.

Закон всемирного тяготения содержит обобщенное математическое выражение некоторой единой физической зависимости, исходя из которой, как следствия, можно объяснить очень широкий круг наблюдаемых в природе фактов. В качестве следствий из закона всемирного тяготения могут быть получены и законы Кеплера.

На склоне лет, сидя в саду за чаем со своими близкими, Ньютон вдруг вспомнил, как много лет назад, в похожей обстановке, падающее на землю яблоко навело его на мысль об общности закона, управляющего и падением яблока, и движением Луны вокруг Земли. Со слов племянницы Ньютона эту историю поведал миру Вольтер, и она стала настолько популярной, что имя Ньютона и закон всемирного тяготения доныне неотделимы от падающего яблока.

Внешне жизнь Ньютона небогата событиями. Она протекала в основном спокойно, мирно и однообразно. Исаак Ньютон родился в Англии, в деревушке Вульсторп, ровно через 100 лет после смерти Коперника в 1643 г.

В 18 лет он поступил учиться в Кембриджский университет, но его занятия были неожиданно прерваны страшной эпидемией чумы, от которой в одном только Лондоне за лето 1665 г, погибла 31 тысяча жителей. Полный новыми знаниями и новыми мыслями студент Ньютон вернулся в Вульсторп и провел в вынужденном «творческом отпуске» около двух лет. Этот «отпуск» имел колоссальное значение для Ньютона, так как именно в это время в его сознании оформилось большинство идей, разработке которых он посвятил всю последующую жизнь. В 1665 - 1667 гг., когда Ньютону не исполнилось еще и 25 лет, он подошел к закону всемирного тяготения.

Ньютон закончил университет, и в последующем занимался научными исследованиями и немного преподаванием, хотя педагогом он был плохим.

Ньютон никогда не был женат, никогда не выезжал за пределы Ангдир. Большую часть времени он обычно бывал погружен либо If опыты, либо в раздумья и вообще казался окружающим рассеянным и молчаливым. Непродолжительное время Ньютон был членом парламента от университета, и предание сохранило анекдот о том, что депутаты услышали его голос лишь один раз, когда он попросил привратника закрыть форточку, чтобы выступающие не простудились.

Уже будучи признанным ученым, в возрасте 53 лет, Ньютон получил пост хранителя, а впоследствии главного директора Монетного двора. Талант Ньютона проявился и в реорганизации монетного дела Англии, которое оказалось поставленным настолько хорошо, что через века стало основой дальнейшей экономической экспансии английского капитализма.

В 1703 г. Ньютон был избран президентом Королевского общества (Название Королевского общества носит английская Академия наук. )и оставался им до конца жизни. В 1705 г. королева пожаловала ему дворянский титул, и он стал именоваться сэром Исааком. Ньютон умер в 1727 г., в возрасте 85 лет, и был похоронен в Вестминстерском аббатстве, национальном английском пантеоне. «Здесь покоится все, что было бренным в Ньютоне» - гласит одна из надписей на его памятнике. В другой надписи процитирована строка из Лукреция: «Разумом он превзошел род людской».

Биографы Ньютона соревновались в придумывании превосходных степеней в оценке его деятельности. Но вряд ли можно оценить ее проще и лучше, чем это сделал сам Ньютон незадолго до смерти: «Не знаю, чем я могу казаться миру, но сам себе я кажусь только мальчиком, играющим на морском берегу, развлекающимся тем, что от поры до времени отыскиваю камешек более цветистый, чем обыкновенно, или красивую раковину, в то время как великий океан истины расстилается передо мной неисследованным».

В науке Ньютон, подобно Копернику, объединил разрозненные представления своих предшественников и, опираясь на плечи исполинов, создал общую физическую концепцию, заставив физику на протяжении последующих 300 лет говорить его языком.

Подобно Копернику, Ньютон очень придирчиво относился к результатам своей научной работы. Если исследованиями проблемы тяготения Ньютон занимался в 1665 - 1667 гг., когда ему не исполнилось еще 25 лет, то опубликован закон всемирного тяготения был 20 лет спустя. Книга «Математические начала натуральной философии», принесшая ее автору славу одного из величайших ученых всех времен, вышла в свет лишь в 1687 г., когда Ньютону было уже 45 лет.

Так же как и у Коперника, у Ньютона был свой «добрый гений», молодой, полный энтузиазма помощник, который всеми силами способствовал завершению и публикации труда своего великого соотечественника. Это был блестящий астроном Эдмунд Галлей, известный в астрономии несколькими важными открытиями. В частности, он открыл собственные движения «неподвижных» звезд и периодичность возвращения к Земле кометы, получившей впоследствии его имя.

Человек в высшей степени разносторонний, Галлей был создателем таблиц страхования жизни* редактировал классические тексты и отыскал место высадки в Британии Юлия Цезаря. На 65-м году жизни он был назначен королевским астрономом и не испугался избрать своей первой целью наблюдения Луны в течение 18-летнего цикла движения ее оси. Эти наблюдения он и довел в действительности до конца. Таким был тот, кто убедил Ньютона издать свой труд и взял на себя его редактирование.

Из-за отсутствия у Королевского общества денег Галлей отдал на издание книги Ньютона собственные сбережения. Он был вовсе небогат и получил от Королевского общества в порядке возмещения затрат сначала 50 экземпляров книги «История рыб», а потом еще 20 экземпляров той же книги.

Закон всемирного тяготения нашел признание далеко не сразу, особенно на континенте. История признания этого закона история геодезических измерений размеров Земли. Выводя одно из следствий закона всемирного тяготения, Ньютон рассуждал примерно следующим образом.

Вообразим, что в теле Земли прорыты две глубочайшие шахты, которые доходят до центра Земли и там соединяются (см. рисунок). Одна шахта прорыта строго вдоль оси вращения Земли, а другая, перпендикулярная к ней,- строго в плоскости экватора. Если такие шахты заполнить водой, то она сможет переливаться из одной шахты в другую и в конце концов займет положение, соответствующее фигуре равновесия.

Если бы Земля не вращалась вокруг оси, на воду в шахтах действовали бы совершенно одинаковые силы тяготения, и в обеих шахтах ее уровень установился бы на одинаковом расстоянии от центра. Фигура равновесия имела бы в этом случае форму шара.

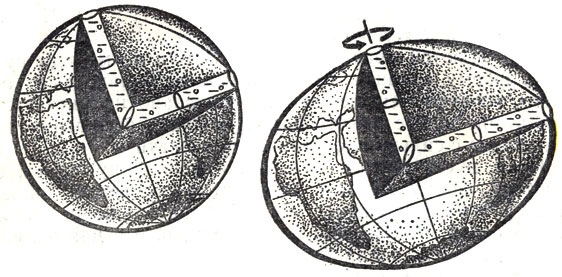
Рассуждение Ньютона о фигуре равновесия вращающейся Земли

Схема поясняет принцип определения фигуры Земли из измерений двух дуг меридиана в 1° на разных широтах

Однако Земля не неподвижна, она вращается вокруг своей оси. При этом вода в экваториальной шахте приобретает центростремительное ускорение, За счет этого давление воды на дно в экваториальной шахте меньше, чем в осевой шахте. Понятно, что равновесие наступит лишь в том случае, когда в экваториальной шахте уровень воды повысится.

Таким образом, закончил свои рассуждения Ньютон, Земля, представляющая собой фигуру равновесия, должна иметь утолщение на экваторе или, что то же, быть сплюснутой у полюсов,

Приведенные рассуждения Ньютона показывают, что он впервые рассмотрел поверхность Земли как поверхность фигуры равновесия. При этом он предполагал, что плотность всех частей Земли одинакова, т. е. Земля является телом однородным. Считая Землю состоящей из бесконечного множества отдельных частичек, он, как это следует из закона всемирного тяготения, полагал, что каждая частичка притягивает к себе все остальные и в свою очередь притягивается ими.

Из теоретических расчетов на основе сделанных предпосылок следовало, что расстояние от центра Земли до полюса должно быть на 0,43% (около 28 км) короче расстояния от центра до экватора.

Теоретический вывод Ньютона оспаривался многими его современниками, которые считали, что Земля в целом либо имеет форму правильного шара, либо не сжата, а, напротив, вытянута у полюсов и имеет форму яйца. «Облатум сиве облонтум» - «сжатая или вытянутая».-- вот спор, который оказался в центре внимания науки на рубеже XVII и XVIII вв. Решить этот спор могли только геодезисты.

Если Ньютон прав, то сечение Земли по меридиану должно иметь форму эллипса. Конечно, земной эллипс сжат очень немного, гораздо меньше, чем это показано на рисунке. Но для того чтобы лучше понять последующие рассуждения, использован эллипс с сильно преувеличенным сжатием.

Итак, пусть сечение Земли по меридиану имеет, согласно Ньютону, форму эллипса. Тогда дуги, соответствующие разности широт в 1°, в разных частях эллипса уже не будут равны между собой. На рисунке хорошо видно, что для эллипса, сжатого у полюсов, полярная дуга должна быть немного длиннее, чем экваториальная. Если бы Земля имела форму яйца, то сечение по меридиану тоже имело бы форму эллипса, но в этом случае полярная дуга оказалась бы короче экваториальной.

Таким образом, перед геодезистами встала ясно сформулированная задача. Необходимо с максимальной точностью измерить две дуги меридиана: одну на севере, ближе к полюсу, другую на юге, ближе к экватору, после чего сравнить их. В случае, если полярная дуга окажется длиннее экваториальной, прав Ньютон. Если же полярная дуга окажется короче, то, следовательно, Земля имеет форму яйца.

Точные измерения протяженных расстояний по пересеченной местности всегда вызывали большие трудности и не могли выполняться с требуемой точностью. Удачный метод измерения больших расстояний удалось дать примерно за полвека до описываемых событий, в 1614 г., голландскому астроному и математику Снеллиусу, предложившему пользоваться для этой цели цепочками треугольников. Слово «треугольник» звучит по-латыни как «триангулум», а поэтому метод. Снеллиуса получил название триангуляции.

Математические основы триангуляции крайне просты. Всякий плоский треугольник, как известно, состоит из шести элементов: трех сторон и трех углов. Если в треугольнике даны одна сторона и два угла, то такой треугольник можно «решить», т. е. исходя из известных элементов с помощью определенных формул вычислить величины неизвестных элементов. То же самое относится и к так называемым сферическим треугольникам, т. е. треугольникам, построенным на поверхности шара. Отсюда нетрудно понять существо метода триангуляции.

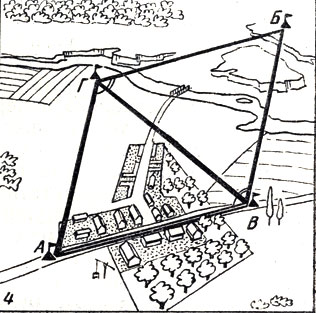
Пусть необходимо измерить расстояние между флажками, поставленными в точках А и Б (см. рисунок). Чтобы выполнить такое измерение непосредственно, потребовалось бы снести значительную часть домов, вырубить в лесу просеку, засыпать овраг и построить мост через реку. Стоимость всех этих работ выразится огромным числом. На их выполнение уйдет немало времени.

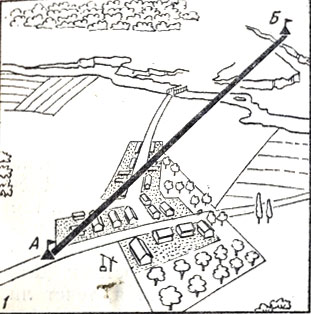
Использование метода триангуляции для измерения больших расстояний на пересеченной местности с естественными преградами

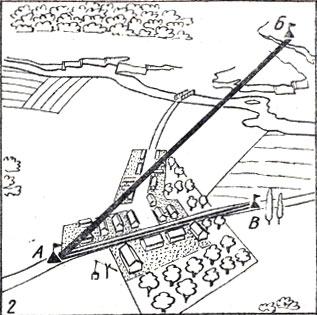
Использование метода триангуляции для измерения больших расстояний на пересеченной местности с естественными преградами

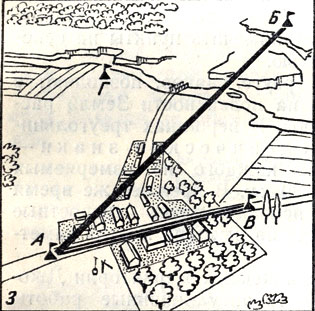
Использование метода триангуляции для измерения больших расстояний на пересеченной местности с естественными преградами

Использование метода триангуляции для измерения больших расстояний на пересеченной местности с естественными преградами

Использование метода триангуляции для измерения больших расстояний на пересеченной местности с естественными преградами.

Применение метода триангуляции позволяет обойти эти трудности. Поставим на дороге в точке В еще один флажок и измерим с максимально возможной точностью линию АВ. Дорога на этом участке прямая, ровная, и поэтому измерение может быть выполнено легко. Назовем измеренную линию базисом.

Обследовав местность, отметим флажком еще одну точку Г так, чтобы с нее были хорошо видны флажки в точках А, Б и В. Теперь пункты А, В и Г образуют на поверхности Земли треугольник, в котором сторона АВ известна. Остается измерить два угла, например в точках В и Г, после чего, решив треугольник, можно получить длины сторон АГ и ВГ и величину угла в точке Л. Получив длину стороны ВГ, будем действовать дальше и измерим в точках В и Г два угла треугольника ВГБ. Зная 1 длину стороны ВГ и значения углов в точках В и Г, отмеченные на рисунке двойной дужкой, вычислим длины сторон ВБ и ГБ и величину угла в точке Б. Таким образом, на поверхности Земли будут построены два треугольника АВГ и ВГБ, в которых известны все углы и все стороны. Теперь вычислим искомое расстояние АБ, и поставленная задача разрешена.

Основное достоинство триангуляции заключается в том, что она сокращает до минимума дорогостоящие и исключительно трудоемкие линейные измерения. Они сводятся лишь к определению длины базиса, причем базис может быть выбран там, где его легче всего измерить. Наибольший объем работ в триангуляции составляют не линейные, а угловые измерения, выполнение которых сопряжено с гораздо меньшими трудностями. Для угловых измерений не имеет существенного значения, течет ли между пунктами река, растет ли кустарник или расположен глубокий овраг. Важно только, чтобы из одного пункта можно было беспрепятственно видеть другой. А этого, как правило, всегда можно добиться, если заранее намечать пункты на основе подробного знакомства с местностью.

Цепочки, состоящие из многих треугольников, позволяют с очень высокой точностью измерять на поверхности Земли расстояния в сотни и тысячи километров. В вершинах треугольников теперь строят специальные геодезические знаки-вышки, благодаря которым стороны каждого из измеряемых треугольников могут достигать 20 - 30 км. В прежнее же время в качестве пунктов триангуляции использовались крепостные башни, колокольни и другие стоящие на высоких местах заметные сооружения.

Под руководством директора Парижской обсерватории Джованни Доменпко Кассини большие триангуляционные работы еще при жизни Ньютона выполнялись во Франции вдоль Парижского меридиана. Но эти измерения, затянувшиеся на долгие годы, так и не разрешили ожесточенного спора о форме нашей планеты. Кассини до самой смерти оставался яростным противником «сплюснутой» Земли. Той же ошибочной точки зрения придерживался и унаследовавший пост директора Парижской обсерватории Кассини-сын.

Окончательно вопрос о форме Земли был решен только в результате триангуляционных измерений двух дуг, расположенных в таких местах, где разность длин одного градуса меридиана наиболее заметна: одной - вблизи экватора и другой - по возможности близкой к полюсу.

Весной 1735 г. парусный фрегат, на борту которого находились французские академики Бугер, Кондамин, Годен и их помощники, взял курс на Перу. А через год, в 1736 г., Францию покидали академики Мопертюи, Клеро, Камюз, Лемонье и шведский физик Цельсий. Их путь лежал на север в далекую, занесенную снегом Лапландию. Там, на границе Швеции и Финляндии, в долине реки Торнео должна была измеряться северная дута.

Подробное описание работы этих двух экспедиции, навсегда вошедших в историю науки, читается как захватывающая повесть. Нестерпимая жара перуанских Кордильер, тропические ливни, лихорадка и нападения индейцев - вот с чем столкнулась экспедиция Бугера. Непроходимые болота, сырой промозглый туман и лютая стужа выпали на долю экспедиции Мопертюи.

Первой закончила свою работу северная экспедиция. И уже сравнения ее результатов с результатами прежних измерений на территории Франции оказалось достаточным, чтобы доказать реальность сжатия Земли у полюсов.

Вернувшийся в Париж в меховой, невиданной французами лапландской шапке Мопертюи был принят как национальный герой. Это был тот самый человек, который, по выражению Вольтера, «приплюснул Землю и всех Кассини». В честь Мопертюи была выбита золотая медаль, на которой он изображен в этой шапке, закутанный в меха, с палицей Геркулеса в одной руке и сплюснутой Землей в другой.

Впрочем, вскоре, поссорившись с Мопертюи, тот же острослов Вольтер не преминул кольнуть его язвительной эпиграммой:

Посланец физики, отважный мореход,
Преодолев и горы, и моря,
Влача квадрант средь снега и болот,
Почти что превратившись в лопаря,
Узнал ты после множества потерь,
Что знал Ньютон, не выходя за дверь!

Полувековой труд французских академиков окончательно доказал, что форма Земли, согласно Ньютону, соответствует фигуре, которая получается путем вращения эллипса вокруг его малой оси. Такая фигура называется в геометрии эллипсоидом вращения, или же просто двухосным эллипсоидом.

По результатам французских измерений можно было заключить, что в среднем полярная полуось Земли на 25 км короче экваториальной.

Сформулированный Ньютоном закон всемирного тяготения оказал огромное влияние не только на развитие физики, но и на развитие астрономии. Изучение движения небесных тел на основе закона всемирного тяготения и законов классической механики стало особой ветвью астрономической науки - небесной механикой. Словно бы оправдываясь за излишнюю полемическую горячность своих предшественников, не признававших закона всемирного тяготения, новое поколение французских ученых внесло неоценимый вклад в небесномеханические исследования. Важных результатов в теоретическом анализе движений планет и комет добились французы Клеро, Даламбер и Лагранж. Большим успехом небесной механики стало удачное предсказание момента возвращения к Земле периодической кометы Галлея.

Французы не были одиноки в развитии этой области астрономии. Российский академик Леонард Эйлер подвел итоги в задаче об определении положений Луны, детально разработав новую точную теорию движения этого небесного тела. Эйлер, крупнейший математик и механик своего времени, обогатил небесную механику многими новыми математическими приемами. Способствовал развитию небесной механики и великий немецкий математик Карл Фридрих Гаусс.

Фундамент небесной механики в том виде, как она теперь существует, был окончательно завершен в самом начале XIX в. в работах современника и участника Великой французской революции Пьера Симона Лапласа.