КАК НЕ СДЕЛАТЬ ИЗ МУХИ СЛОНА

Писатель Эдгар По - любитель леденящих кровь сюжетов - описывает обман зрения, причинивший мучительные терзания герою его рассказа «Сфинкс».

«...На закате жаркого дня я сидел с книгой в руках у раскрытого окна, из которого открывался вид на отдаленный холм за рекой... Подняв глаза, я случайно взглянул на обнаженный склон холма и - увидел нечто странное: отвратительное чудовище быстро спускалось с вершины холма...»

Вид чудовища поверг рассказчика в трепет. Туловище его имело форму клина. Оно было снабжено двумя парами крыльев - каждое по сто метров в длину. Пасть животного помещалась на конце хобота в двадцать метров длиной и такой же толщины, как тело слона. У основания хобота топорщилась густая масса всклокоченных волос, а из нее выдавались, изгибаясь вниз и вбок, два блестящих клыка.

«...Нервы мои не выдержали, и когда чудовище исчезло у подошвы 1йлма в лесу, я без чувств повалился на пол...»

Появление «чудовища» объяснялось просто. Паук укрепил на окне свою паутину. Бабочка-сфинкс спускалась по паутинке вниз прямо перед глазами утомленного героя. А он решил, что животное движется по склону холма. Из-за такого смещения размеры бабочки оказались чудовищно преувеличенными.

Подобный обман зрения знаком, наверное, всякому, и любой сможет рассказать один-два особенно запомнившихся ему случая.

Некоторое отношение может иметь это и к астрономии. Ведь зная массу и наблюдаемую яркость звезд, астрономы вычисляют их плотности и реальные яркости, используя независимо от этого выполненные измерения расстояний. Но не происходит ли с ними того же недоразумения, что и с героем Эдгара По? Может, белые карлики - вовсе не карлики, а просто-напросто очень далекие звезды? А красные гиганты - вовсе не гиганты, а просто близкие звезды? Не делают ли, подобно герою Эдгара По, астрономы из мухи слона?

Правильно измерить расстояния до звезд - это значит правильно оценить их размеры, физические особенности, правильно представить строение Галактики. Как же это делается?

В. Я. Струве первым сумевший измерить расстояние до звезды, использовал для этой цели метод, по своему принципу очень напоминающий метод триангуляции. Базисом для такой «небесной триангуляции» служит диаметр земной орбиты. Рассмотрим чертеж (см. стр. 146).

Пусть буквой С обозначено Солнце, а кружок вокруг него изображает орбиту Земли. Буквой А мы обозначим близкую звезду, расстояние до которой требует определения. Звезды 1 и 2 принадлежат к многочисленным гораздо более далеким звездам. Их зовут звездами фона.

Когда Земля находится в положении I, близкая звезда А видна рядом со звездой 1. Через полгода Земля придет в противоположную точку орбиты, в положение II. Вследствие относительной близости к Солнцу звезда А «сместится» и окажется уже рядом со звездой 2. По величине кажущегося смещения звезды и оценивается расстояние до нее.

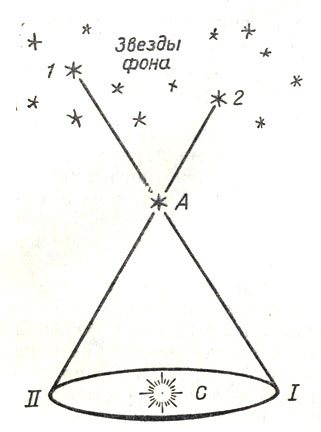
Определение расстояний до ближайших звезд по их смещению относительно гораздо более удаленных звезд фона

Смещения звезд за счет орбитального вращения Земли вокруг Солнца очень малы. Ближайшая соседка Солнца - слабенькая звездочка из созвездия Центавра, названная Проксимой, что в переводе с греческого и значит «ближайшая». Ее смещение за счет движения Земли составляет 1,5".

Вы хотите представить себе, что это за величина? Воткните на расстоянии 1 мм друг от друга две булавки. Привяжите я каждой булавке по нитке. Отойдите от них на 130 м. Соедините свободные концы ниток. Угол, образовавшийся при этом между двумя нитками, и будет равен 1,5" дуги.

Лишь в середине XIX в. астрономическая техника «доросла» до измерения столь малых величин. Первые измерения расстояний до звезд, кроме России, были почти одновременно произведены в Германии и на обсерватории мыса Доброй Надежды в Африке.

Как бы ни были велики размеры отдельных звезд, расстояния между ними несравненно больше. По этой причине в любой из земных телескопов все звезды видны как точки. Сколь бы-громаден ни был телескоп, сколь бы сильно он ни увеличивал, сколь бы ни велики были звезды,- все равно они видны как точки.

Для указания расстояний между звездами, как мы знаем, пришлось ввести специальную единицу длины - световой год.

Для обычных земных представлений световой год - расстояние несказанно большое. «Самолетом будущего» называют первый в мире советский сверхзвуковой трансконтинентальный пассажирский лайнер ТУ-144. Если скорость первого реактивного пассажирского самолета ТУ-104 составляла 800-850 км/час, то стремительный ТУ-144 покрывает 2500 км/час. Представим же себе для сравнения, что какой-то летательный аппарат отправился в полет к звездам со скоростью ТУ-144. Чтобы преодолеть расстояние между Землей и Солнцем, ему понадобится 7 лет. А чтобы достичь Проксимы Центавра, такому аппарату придется затратить почти 2 млн. лет.

Вот список ближайших к Солнцу звезд:

Проксима Центавра - 4,2 световых года,

Альфа Центавра - 4,2 световых года,

звезда Барнарда - 5,9 световых года,

белый карлик Вольф 359 - 7,5 световых года.

Однако подавляющее большинство звезд Галактики удалено от нас на несравненно более значительные расстояния.

В 1967 г. в США торжественно отмечалась 261-я годовщина со дня рождения ученого и борца за независимость североамериканских колоний Бенджамина Франклина. Как водится, чтобы отметить такую годовщину со дня рождения, испекли пирог, в который вставили 261 свечу. Свечи были зажжены с помощью специального электронного механизма. Механизм включился от света звезды v (гамма) Андромеды. Расстояние этой звезды от нас -261 световой год. Луч света, который зажег традиционный пирог, был «ровесником» Франклина. Он отправился в путь через межзвездное пространство в год его рождения.

Расстояния, о которых идет пока речь, установлены путем измерения смещений звезд. Таким способом измерены на сегодня расстояния примерно до 6 - 7 тыс. звезд. Но чем дальше звезды, тем меньше их смещения. Измерять очень малые смещения в конце концов становится невозможным. Метод смещений применим только при расстояниях не больше 300 световых лет. А как же поступать с более далекими объектами? Ведь размеры Галактики значительно больше. А как определять расстояния до других галактик?

Вот тут-то и пора, наконец, вспомнить о звездах, меняющих свой блеск.

Глаз Медузы «моргает» нам из-за того, что одна звезда периодически затмевает другую, более яркую. Звезды такого типа именуют затменно переменными.

Но далеко не все из переменных звезд - затменные.

«Моргает» и звезда 6 (дельта) Цефея. Только причина в этом случае совсем иная. Звезда б Цефея относится к разряду физически переменных - она пульсирует. Яркость физически переменных звезд действительно меняется: звезда набухает - и яркость растет, звезда «худеет» - и тускнеет. Все физически переменные звезды, которые ведут себя подобно б Цефея, повелось называть цефеидами. Цефеиды широко распространены во Вселенной. Их находят повсюду: в различных звездных скоплениях, в чужих галактиках.

В начале XX в. на Гарвардской обсерватории в США принялись за изучение цефеид в звездном скоплении, известном под названием Малого Магелланова Облака. Магеллановы Облака - Большое и Малое - не видны с территории СССР. Они расположены в южной части неба и выглядят как отдельные кусочки Млечного Пути. На самом деле это сравнительно небольшие и удаленные системы звезд, которые находятся за пределами нашей Галактики. Но Магеллановы Облака связаны с Галактикой: они являются как бы сопровождающими ее спутниками.

Казалось бы, изучение цефеид в Магеллановом Облаке не предвещало удивительных открытий. И задача-то была простая. Требовалось уточнить периоды изменения яркости цефеид. Для каждой цефеиды этот период строго постоянен, а от звезды к звезде меняется: период изменения яркости может составлять от нескольких дней до сотен дней и больше.

Но вдруг внимание астрономов привлекло странное обстоятельство. Чем длиннее оказывался период изменения яркости цефеиды, тем ярче была сама звезда. О чем это говорит?

Малое Магелланово Облако находится настолько далеко от нас, что все его звезды можно считать практически одинаково удаленными. Представьте себе лыжника, спешащего вечером по заснеженной долине. Вот он выскакивает на перевал и видит где-то далеко-далеко впереди огни поселка. Строго говоря, каждый дом поселка, каждый из огоньков находятся от лыжника на разных расстояниях. Но расстояния между домами настолько малы по сравнению с общим расстоянием до поселка, что человек вправе считать их одинаково удаленными. А тогда можно сделать вывод: чем ярче светит огонек, тем более яркой лампочкой пользуется хозяин дома.

Если бы лыжник стоял уже на улице поселка, то такого вывода сделать было бы нельзя. Тогда главную роль играло бы расстояние: чем ближе дом, тем ярче свет. Но пока лыжник смотрит на поселок издалека, со стороны, наблюдаемая им яркость огоньков соответствует действительной силе источников света.

Это рассуждение справедливо и по отношению к цефеидам в удаленном звездном скоплении. Стало быть, заключили астрономы, чем ярче на самом деле пульсирующая звезда, тем длиннее период изменения ее яркости. То же подтвердили срочно сделанные наблюдения и над другими звездными скоплениями. Так была обнаружена зависимость между периодом «моргания» цефеид и их реальной яркостью.

Перед астрономами открылись необычайные возможности. Найдены на небе две цефеиды с одинаковым периодом «моргания», но одна в четыре раза слабее другой. Что это значит? Раз периоды их одинаковы, то и реальная яркость их одинакова. А одна видна слабее другой только из-за удаленности. Яркость света ослабевает пропорционально квадрату расстояния. Если одна из цефеид с равными периодами вчетверо слабее другой, значит, она находится в два раза дальше.

Зная это правило, можно отыскивать расстояние до самых далеких объектов, например других галактик, в которых есть цефеиды, Измерив период изменения яркости цефеиды и сравнив его примерно с таким же периодом другой цефеиды, расстояние до которой известно, определяют расстояние до галактики.

Для того чтобы пользоваться описанным методом, понадобились цефеиды с известными расстояниями. Возникшая ситуация напоминает школьную арифметическую задачу. Гражданин А старше гражданина Б на два года, гражданин Б старше гражданина В на пять лет и т. д. До тех пор, пока мы не узнаем возраста хотя бы одного из них, мы не сможем узнать возраста остальных. И даже не будем знать, молодые ли они люди или старые.

Точно то же и для цефеид. Если мы по периоду найдем, как эта звезда светит на самом деле, то, сравнивая с тем, как она видна на небе, и помня, что ослабление яркости происходит из-за ее удаленности, мы сумеем вычислить расстояние до нее. Но чтобы находить многие расстояния, нужно сперва знать их хотя бы для нескольких цефеид. А еще лучше, поскольку всякие измерения связаны с неминуемыми случайными погрешностями, знать расстояния до многих цефеид. Тогда последующие определения расстояний станут более точными.

Астрономы сумели преодолеть эту трудность, отыскав достаточно много близких цефеид, расстояния до которых определялись обычным методом. И теперь цефеиды служат для определения самых больших расстояний во Вселенной. Их образно окрестили: цефеиды - маяки Вселенной. И действительно - путеводные маяки. Они все время «мигают» нам, и по их «миганию» мы узнаем межзвездные расстояния.

Астрономам в наши дни известны и другие методы оценок расстояний до звезд и чужих галактик. Большие работы по уточнению шкалы межзвездных расстояний издавна проводятся в Москве, в обсерватории Московского Государственного университета, полное название которой - Государственный астрономический институт имени П. К. Штернберга (ГАИШ).