Глава II. Основы математической астрономии

§ 5. Небесные координаты

Для определения видимых положений светил на небе астрономы используют небесные координаты. Прежде чем рассказывать о них, сделаем ряд предварительных замечаний.

Чтобы определить положение точки в пространстве, вводят пространственную систему координат. Для этого через некоторую точку О - начало координат - проводят три взаимно перпендикулярные прямые линии ОХ, OY и OZ, называемые осями прямоугольных координат (рис. 30), и выбирают единицу масштаба. Для определения положения точки М опускают из нее перпендикуляр MN на плоскость XOY. Длина перпендикуляра MN, разделенная на длину единицы масштаба,- одна из координат точки М, называемая ее аппликатой; обозначим ее буквой z. Если точка М расположена над плоскостью XOY - аппликата положительна. У точек же, находящихся под плоскостью XOY, аппликата отрицательна. Далее, из точки N опускаем перпендикуляры NP и NQ на оси ОХ и OY. Отрезок ОР оси ОХ дает нам абсциссу точки М: для этого надо разделить длину отрезка ОР на длину единицы масштаба; абсцисса обозначается буквой х. Для получения третьей координаты, называемой ординатой точки М, надо разделить отрезок OQ на ту же единицу длины масштаба; ордината обозначается буквой у. Три величины, ж, у и z, называются прямоугольными координатами точки М относительно осей OXYZ.

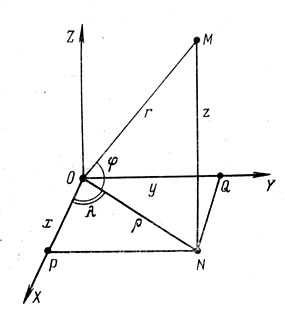
Рис. 30. Пространственная прямоугольная и сферическая системы координат

Можно поступить и иначе. Соединим точки О и М лучом зрения ОМ. Его часто называют радиусом-вектором точки М и обозначают его длину через г. Все точки, имеющие одно и то же значение г, лежат на поверхности шара, у которого центр находится в начале координат О, а радиус равен г. Чтобы выделить на этом шаре нужную нам точку М, определим еще два угла ср и X, которые показаны на рис. 30. Угол φ - это угловое возвышение точки М над плоскостью XOY, а угол λ, = ∠NOP не что иное, как угол между плоскостями NOM и XOZ. Задавая углы λ и φ, мы найдем направление луча ОМ. Чтобы найти на этом луче положение точки М, надо еще задать радиус-вектор r. Итак, в этой системе, называемой системой сферических координат, для определения положения точки М надо задать три величины -две угловые и одну линейную.

Сферические и прямоугольные координаты связаны между собой простыми формулами, которые нетрудно вывести.

Однако для определения видимого положения небесных светил такая система координат, к сожалению, не вполне пригодна. Мы обычно редко знаем расстояния до небесных светил. Поэтому еще в глубокой древности, астрономы ввели понятие о небесной сфере. Мы назовем шаровую поверхность произвольного радиуса, центр которого находится в глазу наблюдателя, небесной сферой. Каждый луч зрения пересекает небесную сферу в определенной точке. Мы будем считать, что небесное светило находится в той точке, в которой луч зрения пересекает небесную сферу. Таким образом, под положением светила мы будем понимать не его истинное положение в пространстве, а то место, которое оно занимает на небесной сфере. Это дает возможность ограничиться двумя угловыми координатами светила.

При установлении небесных координат светил астрономы специальным образом выбирают направления осей X, Y и Z. В этом параграфе мы ограничимся введением горизонтальной системы координат. Установим, как расположены главные точки этой системы.

Подвесим на шнуре небольшой груз и подождем, пока он придет в состояние покоя. Тогда направление висящего шнура совпадает с линией отвеса, которая пересекает небесную сферу в двух точках. Та точка, которая расположена над головой наблюдателя, называется зенитом. Вторая точка, расположенная под ногами наблюдателя (естественно, невидимая), называется надиром.

Изобразим небесную сферу на чертеже таким образом, как будто наблюдатель рассматривает ее со стороны, а не находится в ее центре, о чем надо хорошо помнить, рассматривая рисунок (рис. 31). На этом рисунке зенит обозначен буквой Z, а надир - буквами Na. Теперь проводим через центр О небесной сферы, т. е. через глаз наблюдателя, плоскость, перпендикулярную к линии отвеса ZO. Это - плоскость математического горизонта. Она пересекает небесную сферу по большому кругу, который называется математическим горизонтом. (Заметим, что большим кругом является такой круг, который делит небесную сферу пополам.) Математический горизонт разделяет небесную сферу на две полусферы. Полусфера, расположенная под математическим горизонтом, скрыта под поверхностью Земли и для наблюдателя невидима.

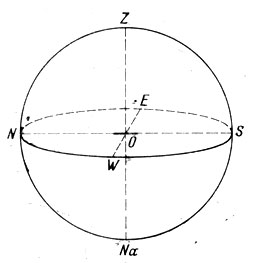
Рис. 31. Зенит, надир и другие точки горизонтальной системы координат

После этого находим на математическом горизонте точки юга, запада, севера и востока. Основной точкой на математическом горизонте является точка юга S. Как ее найти?

Казалось бы, самый простой способ состоит в использовании компаса. Однако это не так и вот почему. Известно, что магнитный меридиан не совпадает с географическим, и стрелка компаса не указывает точно на точку юга. Более надежный способ связан с наблюдением суточного движения Солнца. В истинный полдень Солнце находится строго над точкой юга и достигает наибольшего возвышения над горизонтом. В этот момент все тени вертикальных предметов становятся наиболее короткими и направлены строго на точку севера. Достаточно проследить за тенью, отбрасываемой вертикальным колышком - гномоном (рис. 32).

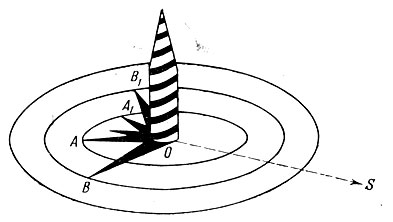
Рис. 32. Гномон и определение направления точки юга

Таким образом, в момент истинного полдня тень гномона расположится вдоль линии «юг - север», которая называется полуденной линией. Следовательно, зная момент истинного полдня (см. §§ 13 и 14) и пронаблюдав за тенью гномона, мы отыщем положение полуденной линии (рис. 32). Найдя же положения точек юга S и севера N, мы определим также положение на математическом горизонте точки запада W и точки востока Е (см. рис. 31).

Установив положение точки юга, проведем плоскость через нее, центр небесной сферы и зенит; мы получим плоскость небесного меридиана. Пересечение этой плоскости с небесной сферой дает большой круг NZSNa проходящий через точки N, Z, S, Na и называемый небесным меридианом. Когда небесное светило в своем суточном движении пересекает небесный меридиан, говорят, что оно кульминирует.

Проведем теперь плоскость через центр небесной сферы, зенит и точки востока Е и запада W. Это - плоскость первого вертикала. Большой круг, по которому эта плоскость пересекает небесную сферу, называется первым вертикалом.

Плоскости математического горизонта и небесного меридиана являются основными в горизонтальной системе координат (рис. 33). Пусть светило находится в точке Q небесной сферы. Проведем луч зрения OQ и построим плоскость, проходящую через линии OZ и OQ, т. е. через линию отвеса и луч зрения. Эта плоскость называется плоскостью вертикала светила. Она пересекает небесную сферу по большому кругу ZQK, который называется вертикалом светила. Отметим точку пересечения вертикала светила с математическим горизонтом буквой К. Тогда дуга большого круга KQ, измеряющая угол KOQ, равна угловому возвышению светила над горизонтом и называется высотой светила Н. Если светило находится на горизонте, то его высота равна нулю; если же оно находится в зените, то h =+ 90°. У светил, находящихся под горизонтом, высота отрицательна (h <0°). Высота светила непосредственно измеряется специальными угломерными инструментами, например, теодолитами. Для того же, чтобы определить высоту Солнца, вполне достаточно гномона (рис. 34); зная его длину А В и длину отбрасываемой тени ОБ, мы можем найти из треугольника АОВ, что tgh=АВ/ОВ где h - высота Солнца Астрономы обычно измеряют не высоту светила, а его зенитное расстояние z, т. е. угол ∠ZOQ между лучом зрения и линией отвеса или дугу ZQ (см. рис. 33). Очевидно, что справедлива формула z + h = 90>^о.

Светила, обладающие одной и той же высотой, располагаются на малом круге небесной сферы, плоскость которого параллельна плоскости математического горизонта. Мы будем называть его кругом равных высот.

Для определения второй координаты, которая позволила бы установить, в какой точке круга равных высот находится данное светило, надо измерить угол между плоскостями вертикала светила и небесного меридиана. Этот угол измеряется дугой горизонта SK, заключенной между точкой юга S и точкой К пересечения вертикала светила с горизонтом (см. рис. 33). Его называют азимутом светила и обозначают буквой а. Азимут отсчитывается от точки юга по направлению к западу. Так, например, у точки W он равен 90°, у точки N - 180°, а азимут точки Е равен 270°.

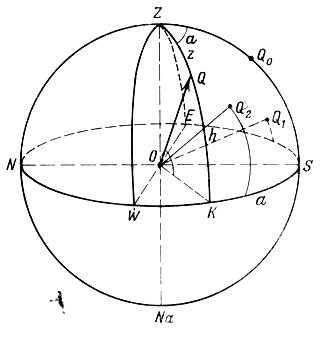
Рис. 33. Горизонтальная система координат (у точки Qо азимут равен нулю)

Итак, два числа - азимут и зенитное расстояние (или азимут и высота), называющиеся горизонтальными координатами, дают возможность разыскать нужное нам светило.

Например, пусть задано, что в некоторый момент времени светило имеет азимут а = 72° и зенитное расстояние z = 34°. Как отыскать его на небе?

Поворачиваемся лицом к точке юга; затем от этой точки поворачиваемся к западу на угол, равный 72°. Теперь мы обращены лицом к точке пересечения вертикала светила с горизонтом. Вычитаем из 90° величину зенитного расстояния, получаем для высоты светила 56° и, подняв наш взор на этот угол над горизонтом, мы найдем нужное нам светило.

Для определения горизонтальных координат светил служит особый прибор, называемый универсальным инструментом. Этот прибор состоит из зрительной трубы, которая может вращаться вокруг горизонтальной оси, снабженной разделенным кругом. Наведя трубу на светило, мы берем по вертикальному разделенному кругу отсчет. Это или высота, или зенитное расстояние. Горизонтальная ось укреплена в стойке, которая позволяет вращать инструмент вокруг вертикальной оси, т. е. изменять азимут. Беря отсчет горизонтального круга, мы определяем и эту координату.

Заканчивая описание горизонтальных координат, заметим, что светило, находящееся в зените и имеющее зенитное расстояние равное нулю, не имеет азимута. Зенит и надир - две «особые» точки этой системы координат.

Прежде чем перейти к описанию других систем небесных координат, рассмотрим суточное вращение небесной сферы.