§ 7. Экваториальная система координат

Горизонтальные координаты светил - азимуты и зенитные расстояния - непрерывно изменяются. Астрономы же нуждаются в таких координатах небесных светил, которые не изменялись бы со временем (по крайней мере, не изменялись бы быстро). Поэтому астрономы были вынуждены искать другие системы небесных координат. Так была введена система, у которой главная плоскость - плоскость небесного экватора.

На рисунке 36 изображены линия отвеса OZ и математический горизонт SWNES. На нем также показано расположение оси мира РР' - оси экваториальной системы координат. Проходящая через центр небесной сферы, перпендикулярно к оси мира, плоскость небесного экватора пересекает небесную сферу по большому кругу HWH'EH. Это и есть небесный экватор. Проведем из центра небесной сферы луч зрения OQ. Затем через ось мира и луч зрения проводим плоскость POQ' она пересекает небесную сферу по большому кругу PQKP', который называется кругом склонения светила. Круг склонения PQKP' пересекает небесный экватор в точке К. Угол между линиями ОК и OQ, измеряющийся дугой KQ, называется склонением светила и обозначается греческой буквой дельта (б). У светил северного небесного полушария склонения положительны, у светил южного полушария - отрицательны. Таким образом, склонения заключены в пределах от -90° до +90°. Иногда вместо склонения употребляют полярное расстояние светила, которое измеряется углом между осью мира ОР и лучом зрения OQ. Полярное расстояние заключено в пределах от 0° до 180°. Все небесные светила, имеющие одинаковое склонение, находятся на одной суточной параллели и, очевидно, при вращении небесной сферы их склонения не меняются.

Чтобы установить вторую координату, рассмотрим две плоскости - плоскость небесного меридиана PZHSO и плоскость круга склонения светила OPQKP'. Они образуют двугранный угол, который измеряется дугой экватора, заключенной между точками Н и К. Эта дуга, отсчитываемая от точки Н в сторону вращения небесной сферы, т. е. к западу, называется часовым углом светила t. Это также угол между касательными к меридиану и кругу склонений при полюсе мира Р. Часовой угол заключен в пределах от 0° до 360°.

Когда светило находится в верхней кульминации, его часовой угол равен нулю. Затем часовой угол возрастает пропорционально времени и когда светило приходит в нижнюю кульминацию, он становится равным 180°. Таким образом, у светил, находящихся к востоку от плоскости небесного меридиана, часовые углы больше 180°.

Итак, мы определили две экваториальные координаты светила - часовой угол t и склонение δ. В этой системе координат склонения звезд остаются постоянными, но часовые углы изменяются. Причина состоит в том, что за начало отсчета часовых углов принята точка Н пересечения небесного экватора с небесным меридианом, не принимающая участия в суточном вращении небесной сферы. Но чтобы иметь обе координаты неизменными, нужно вместо часового угла ввести такую координату, которая отсчитывалась бы от точки экватора, принимающей участие в суточном вращении небесной сферы.

За такую начальную точку приняли точку весеннего равноденствия Т, в которой небесный экватор пересекается с эклиптикой (см. рис. 36). Проведем круг склонения этой точки РТР'. Между плоскостями РТРО и PQKPO образуется двугранный угол, который измеряется отрезком дуги экватора ТК. Этот угол отсчитывается от точки весеннего равноденствия Т против направления суточного вращения небесной сферы, с запада на восток, и называется прямым восхождением светила. Он обозначается греческой буквой альфа (а).

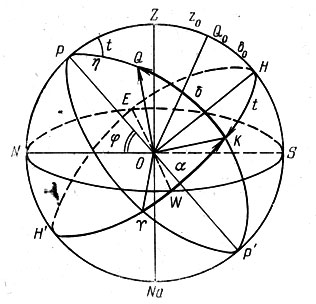
Рис. 36. Экваториальная система координат. Светило Qо кульминирует

Итак, мы определили две координаты светила - прямое восхождение и склонение. Они широко используются в астрономии, в том числе для составления списков звезд - звездных каталогов.

Остается последнее - связать между собой прямое восхождение и часовой угол светила.

Для этого надо ввести понятие о звездном времени. Двугранный угол между плоскостями PHSP'O и Р Р'О, измеряющийся отрезком дуги экватора ТH, измеряет звездное время в данный момент. Иначе говоря, звездное время - это часовой угол точки весеннего равноденствия. Оно обозначается буквой s. Из рис. 36, видно, что дуга Н Т = Т К + КН, а это означает, что справедлива формула s = α + t (2.1)

У астрономов есть специальные часы, которые идут по звездному времени (см. § 12). Зная прямые восхождения светил, нетрудно по формуле (2.1) вычислять их часовые углы. Кстати, заметим, что так как в момент верхней кульминации светила его часовой угол равен нулю, из формулы (2.1) следует, что звездное время равно прямому восхождению кульминирующего светила.

В заключение сделаем еще одно важное замечание. Часовой угол и прямое восхождение могут быть выражены в градусной мере угла. Однако гораздо чаще их выражают в особой «временной» мере. Так как небесная сфера совершает полный оборот на 360° за 24 часа, то за один час она поворачивается на 15°. Нетрудно составить следующую табличку:

1 час - 15° 
1 минута - 15' 
1 секунда - 15"
1° - 4 минуты времени 
1' - 4 секунды времени 
1" - 1/15 секунды времени

Эта табличка помогает переводить часовой угол из одной меры в другую. Напомним, что принято обозначать дуговые меры следующими значками: градус - °; минута дуги -'; секунда дуги -"; меры времени: час - ч. или h; минута времени - м. или т; секунда времени - с. или s. Так, например, 75°15'16"- градусная мера, а 9ч. 18 м. 33 с.- временная мера часового угла.

Иллюстрируем сказанное примером.

Выразим угол 193°18'55" в единицах времени; пользуясь табличкой, находим:

Теперь переведем угол α - 22 ч. 35 м. 55, 85 с. в градусную меру. Пользуемся той же таблицей:

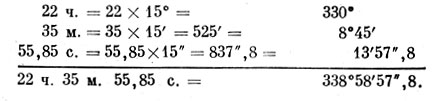
(В книге-источнике отсутствуют страницы: 45-46)