§ 11. Предварение равноденствий (прецессия)

Коснемся теперь одного важного вопроса, без которого ни один астроном не может грамотно пользоваться звездными картами и звездными каталогами.

Уже в древности было обнаружено, что точка весеннего равноденствия медленно перемещается на фоне звезд. Она плавно, на 50" в год, смещается навстречу движущемуся по эклиптике Солнцу. Отсюда и возник «термин «предварение равноденствий». Вызвано это тем, что ось вращения рр' Земли под влиянием лунно-солнечных притяжений описывает в мировом пространстве конус, осью которого является ось эклиптики ЕЕ' (рис. 40). Растворение этого конуса 47°; полный обход конуса завершается за 26 тысяч лет.

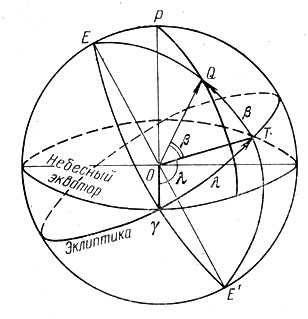
Рис. 38. Эклиптикальные координаты

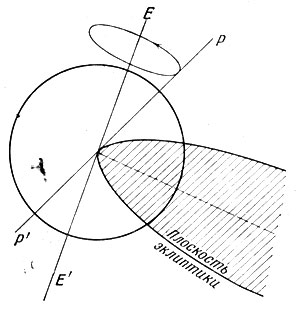
Рис. 40. Обяснение явления прецессии

В результате такого перемещения оси Земли, называемого прецессионным, полюсы мира очень медленно движутся вокруг полюсов эклиптики. На рис. 41 показан путь северного полюса мира. Мы видим, что около 2000 года северный полюс мира находится около а Малой Медведицы, а около 14 000 года он подойдет к Веге!

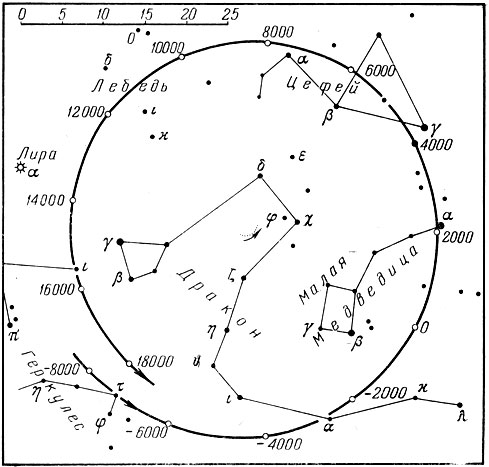
Рис. 41. Путь полюса мира на небесной сфере, описываемый вследствие процессии. Числами указаны годы, соответствующие различным положениям полюса

Теория прецессии чрезвычайно сложна, но нам нет необходимости в нее вдаваться. Нам нужен практический учет влияния прецессии на координаты звезд, чему помогает таблица 5 (стр. 372). Покажем, как ею пользоваться. В таблице 5 две части. В первых 16 столбцах для склонений, заключенных в пределах от -30 до +80°, через каждые 10° приведены годичные изменения прямых восхождений Да для различных а - от О ч. 00м. до 24 ч. 00 м., через 40 минут. В последнем же столбце приведены изменения склонений Δδ. Таким образом, часть таблицы, содержащая Да, имеет два «входа» для интерполирования, а та часть, которая содержит Δδ, - один.

Допустим, что нам известны координаты светила, отнесенные к положению небесного экватора и эклиптики для эпохи каталога 1855 г., которая была принята при составлении Боннского Обозрения. Мы же хотим узнать, какие координаты должно иметь это светило в эпоху 1900 г., т. е. на 45 лет позднее. Для этого надо вычислить годичное изменение координат, умножить его на 45 и придать к координатам эпохи 1855 г.

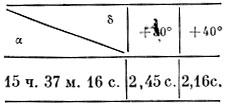
Начнем с обработки склонения светила. Из таблицы 5 видно, что Δδ зависит только от а. Пусть прямое восхождение светила равно 15 ч. 37 м. 16 с.; выписываем из последнего столбца таблицы 5 данные для подходящего интервала:

Прямое восхождение увеличилось на 40 м., а величина поправки Δδ на 2",9. Разделив последнюю величину на 40, мы получим изменение при увеличении α на 1 минуту: +0",0725. Заданное нам прямое восхождение превышает 15 ч. 20 м. на 17 м. 16 с. - - 17,3м.; умножаем на 0,0725 и получаем, приближенно, +1",2. Прибавив эту поправку к величине -12",9, получим Δδ = -11",7. Умножив, наконец, на 45, получим

45Δδ =-11",7 х 45=-526"=-8'46".

Придав ее к склонению звезды, найдем

δ₁₉₀₀=+33^о35'52"-8'46"=+33^о27'06"

Выполненное нами действие называется линейным интерполированием.

Теперь приступим к преобразованию прямого восхождения. Пользование первой частью таблицы 5, содержащей годичные изменения Аа, сложнее, так как таблица имеет два входа. Выпишем

из нее часть, «внутри» которой находятся заданные координат светила:

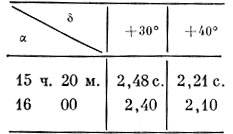
Теперь интерполировать надо в двух направлениях. Допустим сначала, что склонение звезды равно точно +30°, а ее прямое восхождение на 17 м. 16 с. = 17,3 м. больше, чем табличное значение 15 ч. 20 м. Из столбца, соответствующего в последней табличке +30°, находим, что при изменении α на 40 м. Δα уменьшилось на 0,08 с. Разделив на 40, получаем изменение Аа за минуту - 0,002с. Умножив на 17,3, получим 0,03 с., которые вычитаем из 2,48 и получаем 2,45 с.

Теперь производим такое же действие с числами, помещенными в столбце, соответствующем δ = +400. Здесь уменьшение Аа произошло на 0,11 с.; разделив на 40, находим 0,00275. Умножив на 17,3 и вычтя из 2,21, получим 2,16 с. Мы произвели одно интерполирование и его результаты выпишем ниже:

Надо выполнить второе интерполирование, так как заданное нам склонение светила равно 33°35'52" = 33°35',9 = 33°,6 (мы обратили секунды в доли минуты, а затем минуты в доли градуса). Заданное нам значение склонения превосходит табличное на 3°,6. Из таблицы видно, что при увеличении склонения на 10° Аа уменьшается на 0,29 с. Следовательно, при увеличении на 1° оно уменьшится на 0,029 с. Умножив на 3,6, находим поправку 0,10 с, которую и надо отнять от табличного значения 2,45. Получаем 2,35, которые умножаем на разницу эпох, равную 45. Это дает 106 с. = 1 м. 46 с. Прибавляя к заданному прямому восхождению, получаем нужный ответ:

α₁₉₀₀ = 15 ч. 37 м. 16 с.+ 1 м. 46 с. == 15 ч. 39 м. 02 с.

Если надо вычислить положение светила для более ранней эпохи, например, перейти от координат 1950 г. к координатам 1900 г., то надо выполнить те же самые вычисления, но полученные поправки придать с обратным знаком.

Конечно, описанный учет влияния прецессии приближенный, но для наших целей его точность вполне достаточна. Точный учет производится гораздо сложнее. Так, например, для близких к полюсу звезд пользоваться описанным нами способом вообще нельзя. Поэтому таблица 5 не содержит Δα и Δβ для звезд, имеющих склонения больше +80°. В этих местах небесной сферы надо пользоваться точными формулами, так как здесь влияние прецессии сказывается гораздо сильнее.