§ 23. Второй астрономический треугольник

При решении некоторых задач совершенно необходимо знать эклиптика л ьные координаты светила. Поэтому надо уметь их вычислять по прямому восхождению и склонению светила. Для этого построим так называемый второй астрономический треугольник.

Нанесем на небесную сферу небесный экватор НН', полюсы мира Р и Р', эклиптику LM и ее полюсы Е и Е' (рис. 48). Соединим точку Q, в которой находится светило с точками Е и Р дугами больших кругов. Образуется сферический треугольник EPQ. Найдем его элементы.

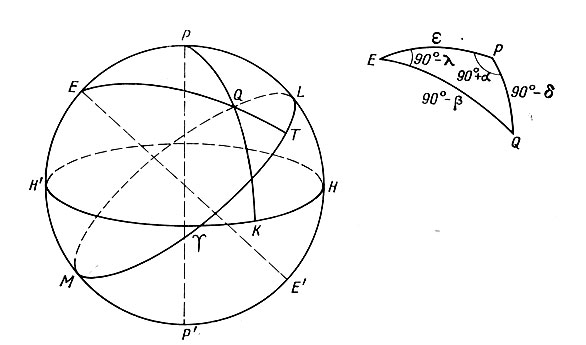
Рис. 48. Второй астрономический треугольник

Сторона ЕР равна наклонению эклиптики к экватору в - 23°27'. Сторона PQ - полярное расстояние светила р = 90°-δ. Третья сторона - угловое расстояние светила от полюса эклиптики EQ = 90° - β, где β - астрономическая широта светила. Эти стороны обозначены в правой части рис. 48.

Несколько сложнее установить углы этого треугольника. Угол при вершине Р измеряется дугой небесного экватора Н'К, которая равна сумме дуг Я' Т и Т К. Первая из них равна 90°, а вторая - прямому восхождению светила а. Итак, ∠Р - 90° + ct. Угол при вершине Е измеряется дугой эклиптики TL, равной разности дуг TL и ТТ. Первая из них равна 90°, а вторая -астрономической долготе Я. Таким образом, ∠Е = 90° - λ.

Если даны ε, α и β, а надо найти Р и А,, то применим первую из формул (2.2) к стороне EQ:

cos (90^о-β) = cos ε cos (90^о - δ) + sin ε sin (90^о - δ) cos (90^о + α)

Согласно формуле(2.3) находим

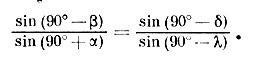
Применив одну из формул группы (2.4). к стороне EQ и углу Е, получим

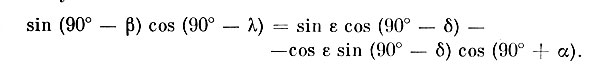
После упрощений получаем необходимые формулы:

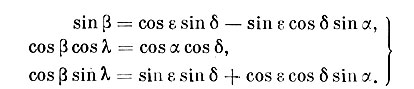
Примера приводить не будем, так как в предыдущем параграфе весь ход вычислений был подробно описан.