§ 69. Расстояния до звезд

Для выяснения физических свойств звезд мы должны прежде всего узнать расстояние до них. Существует несколько способов определения расстояний до звезд. Самый надежный из них - тригонометрический. В его основу положено понятие о годичном параллаксе звезды (рис. 136). Пусть при некотором положении Земли луч зрения АЕ составляет прямой угол с радиусом земной орбиты АС. Тогда угол р, под которым со звезды виден радиус земной орбиты, называется годичным параллаксом звезды. Обозначая радиус земной орбиты через А, а расстояние от Солнца до звезды через D, имеем из прямоугольного треугольника АСЕ формулу А = D sin р, откуда D = A/sin p. Угол p, вообще говоря, очень мал, и его синус можно заменить дугой Р. Найдем зависимость между углом р, измеренным в угловой мере, и соответствующей ему длиной дуги Р, считая, что радиус ее равен единице. Длина окружности единичного радиуса равна 2π = 2 X 3,14 = 6,28. С другой стороны, полная окружность содержит 360°, каждый из которых составляет 3600". Поэтому, выражая р в секундах дуги, можно написать так:

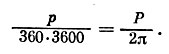
Отсюда, решая пропорцию, находим выражение угла р через соответствующую дугу Р:

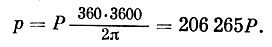
Теперь легко вычислить расстояние до звезды. Подставляя в формулу, определяющую D, значение р, находим

>

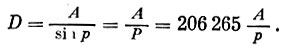Так как А равно 149 600 000 км, а годичный параллакс ближайшей к нам звезды а Центавра равен 0",75, то ее расстояние от нас равно

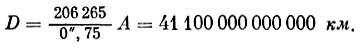
Ввиду того, что выражать расстояния до звезд в километрах очень неудобно, условились применять особую единицу измерения расстояний, которую назвали парсеком. Слово «парсек» происходит от двух слов: «параллакс» и «секунда»; на расстоянии в один парсек годичный параллакс равен одной секунде. Легко вычислить это расстояние. Положим в последней формуле р - i", и тогда 1 парсек = 206265 А = 30 857 000 000000 км.

Помимо парсека, употребляют в качестве единицы измерения расстояний снетовой год - расстояние, которое луч света, распространяющийся со скоростью 300 000 км/сек, пробегает за один год. Если выполнить все вычисления, то мы получим следующую зависимость:

1 парсек = 3,26 светового года.(7.2)

Если выражать расстояние до звезд в парсеках, то формула (7.1) приобретает вид

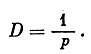
Допустим, что параллакс некоторой звезды равен 0",1. Тогда расстояние до нее равно 10 парсекам, или 32,6 светового года.

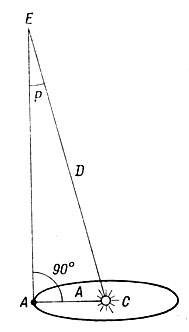
Рис. 136. Годичный параллакс звезды

При перемещении Земли вокруг Солнца по ее орбите видимые положения близких звезд должны немного изменяться: они должны перемещаться на фоне далеких звезд, описывая маленькие эллипсы. Эти смещения очень малы. Оказалось, что у ближайшей к нам звезды параллактическое смещение не превышает 1",5. Только современное развитие техники, а особенно применение фотографии, дало возможность выполнять столь точные измерения, необходимые для определений параллаксов звезд.

Измерения годичных параллаксов в настоящее время выполнены для нескольких тысяч звезд и, следовательно, их расстояния известны.

Можно ли, пользуясь этим методом, определить расстояние до любой, сколь угодно удаленной от нас звезды? Конечно, нет! Дело в том, что точнейшие астрономические измерения не позволяют определять угловых смещений, меньших 0", 005. Это означает, что если параллактическое смещение равно 0", 004, то его уже нельзя измерить. Поэтому для измерения расстояний до очень далеких звезд пользуются другими способами, которые будут описаны дальше.