§ 84. Затменные переменные звезды [1973 Цесевич В.П.

Затменные переменные - одна из разновидностей двойных звезд. Двойная звезда оказывается затменной переменной, если в момент соединения одна из ее компонент частично или полностью закрывает от наблюдателя вторую компоненту. Затмения повторяются периодически, и первая задача наблюдателя состоит в определении точного значения периода Р и момента наступления наибольшей фазы затмения М₀. Если эти значения найдены, то последующие моменты минимумов блеска вычисляются по формуле

где Е - целое число (номер минимума M_E). Предвычисленные моменты минимумов называются эфемеридой.

Следующая задача наблюдателя - построение на основе многих наблюдений кривой изменения блеска звезды. Для этого на горизонтальной оси графика откладывается время, а на вертикальной - звездная величина, либо другая величина, определяющая блеск. Блеск должен возрастать на графике вверх (а звездная величина - вниз).

Подвергая затем полученную кривую изменения блеска математической обработке, исследователь извлекает из нее ряд важных данных, называемых элементами двойной системы. Ему приходится принять радиус относительной орбиты (расстояние между центрами компонент) за единицу; тогда из кривой блеска он получит размеры компонент, выраженные в долях этой единицы, сможет вычислить относительный блеск компонент и установить, чему равно наклонение орбиты к плоскости, перпендикулярной к лучу зрения (картинной плоскости).

Каждая из затменных переменных является также спектрально-двойной. Из определения лучевых скоростей, как мы знаем (§ 74), можно определить размеры относительной орбиты и массы компонент, если знать наклонение орбиты. В данном случае оно известно, и, следовательно, для затменной переменной известны не только радиус относительной орбиты, но и радиусы звезд, а также массы в единицах CGS. Таким образом, затменные переменные - один из источников информации о весьма важных характеристиках звезд.

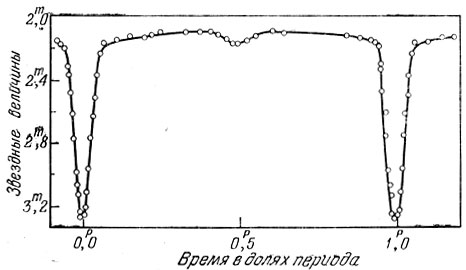
Рис. 169. Кривая изменения блеска Алголя

Класс затменных переменных звезд разделяется в свою очередь на несколько типов.

Особенно многочисленны звезды типа Алголя, кривая изменения блеска которого изображена на рис. 169. Она характеризуется почти постоянным максимальным блеском, прерываемым глубоким первичным минимумом - главным затмением, во время которого яркая компонента скрывается за менее ярким спутником. На кривой виден и вторичный минимум, вызванный затмением спутника яркой компонентой. Затмения повторяются через период, равный 2,867 суток. Оба минимума «острые» - после окончания падения блеска немедленно начинается его подъем, так как происходят частные затмения. Максимальный блеск Алголя пе остается совершенно постоянным, а немного усиливается ко вторичному минимуму и ослабляется после него, что объясняется отражением излучения яркой звезды спутником.

У некоторых звезд типа Алголя происходят полные затмения. Во время полной фазы затмения к нам доходит только тот свет, который излучает спутник, затмевающий яркую звезду. На кривой блеска в ее минимальной части мы находим в этом случае интервал постоянного (минимального) блеска, продолжительность которого позволяет судить о длительности полной фазы затмения. Практика показывает, что при наличии такого интервала элементы системы вычисляются гораздо надежнее, чем из кривых блеска при частных затмениях.

Примером звезды с продолжительной фазой полного затмения может служить красивая затменная звезда U Цефея. Вот краткие данные о ней. Моменты минимумов наступают в соответствии с формулой

Эта формула является численной реализацией формулы (8.1); начальный момент минимума М0 выражен в ней в юлианских днях (§ 18), а период Р - в средних сутках.

Звездная величина этой звезды в максимуме блеска 6^m,63, a в главном минимуме 9^m,79. Вторичный минимум почти незаметен. Главное затмение длится около 10 часов, а его полная фаза - 1,9 часа. Из-за длительности затмения полный минимум в течение одной ночи пронаблюдать не удается. Поэтому кривую блеска приходится строить по наблюдениям, полученным в разные ночи (см. § 89).

Анализ кривой изменения лучевой скорости (рис. 170) и кривой блеска привел к следующим выводам: радиус относительной орбиты (расстояние между центрами компонент) составляет 10,22 млн. км, радиус яркой звезды 2,2 млн. км, а радиус менее яркого спутника - 3,2 млн. км меньшая по размерам яркая звезда излучает 95% света ввей системы, а больший спутник - только 5%!

Масса яркой звезды равна 4,30 массы Солнца, а спутника -2,58; средняя плотность вещества яркой звезды (спектрального класса В8) равна 0,19 г/см³, а спутника (субгиганта спектрального класса G) 0,039 г/см³.

Период звезды оказался переменным (он постепенно увеличивается); поэтому рекомендуем ее регулярно наблюдать (см. § 88). Для этой цели приводим на рис. 171 карту ее окрестностей и звездные величины звезд сравнения, которые необходимы при наблюдениях.

Обратим теперь внимание на поведение лучевой скорости этой звезды во время главного минимума блеска. На рис. 170 кривая лучевой скорости яркой звезды изображена сплошной линией. Ее плавный ход нарушается во время главного затмения. Здесь кривая проведена пунктиром. Это изменение лучевой скорости вызвано орбитальным движением. Штрихами изображена кривая изменения лучевой скорости спутника. Его спектр виден только во время затмения, и потому на рис. 170 изображен только отрезок кривой. В тот момент, когда пунктирная и штриховая линии пересекаются, наступает минимум блеска; в этот момент обе компоненты движутся перепендикулярно лучу зрения и их лучевые скорости должны быть равны нулю.

Однако при наступлении минимума блеска лучевая скорость яркой звезды начинает возрастать и достигать своего наибольшего затмения перед началом полной фазы. Затем плавная кривая разрывается, и после окончания полной фазы затмения наблюдается резкое уменьшение лучевой скорости, которая затем увеличивается, и по окончании затмения влияние «аномалии» прекращается.

Такой сложный вид кривой изменения лучевой скорости вызван сложением двух эффектов - орбитального движения и вращения яркой звезды вокруг ее оси. Дело в том, что перед наступлением полной фазы затмения почти весь диск яркой компоненты закрыт спутником, за исключением узкого серпа, который в результате осевого вращения удаляется от нас. После окончания полной фазы из-за спутника появляется другой край яркой звезды, который к нам приближается. Таким образом, размах разрыва кривой лучевых скоростей позволяет определить скорость вращательного движения на экваторе яркой звезды. Оказалось, что у U Цефея скорость вращательного движения равна 200 км/сек, так что период осевого вращения оказался в 4,5 раза короче периода орбитального обращения.

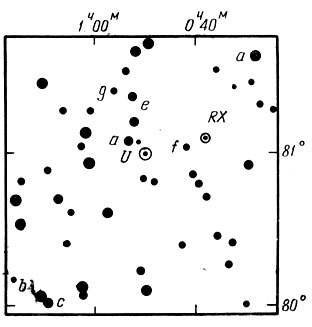
Рис. 171. Карта окрестностей U Цефрея. Звездные величины звезд сравнения: а = 6,38, b = 6,73, с = 7,20, d = 7,80, е = 8,41; f =9,12, g =9,54. На карте помечена также неправильная переменная RX Цефрея

Иногда встречаются звезды типа Алголя, у которых обе компоненты имеют почти равные размеры и блеск. Тогда первичный и вторичный минимумы имеют почти равную глубину, как, например, у WW Возничего. При круговой орбите кривая блеска симметрична, т. е. промежутки времени между первичным и вторичным минимумами блеска, а также между вторичным и последующим первичным - одинаковы и равны половине периода обращения.

Если же орбита эллиптическая, то первичный и вторичный минимумы расположены несимметрично. Такое явление было обнаружено у RU Единорога (рис. 172). Исследовавший эту звезду Д. Я. Мартынов показал, что орбита медленно поворачивается в ее плоскости, и кривая блеска прогрессивно изменяет свой вид. На рис. 172 изображены четыре кривые изменения блеска, совмещенные первичными минимумами. Из него хорошо видно, как за время наблюдений с 1907 по 1965 г. изменялась форма кривой блеска, как смещался вторичный минимум по отношению к первичному. В правой части рисунка изображены различные положения орбиты; мы видим, как перемещалась против часовой стрелки большая ось орбиты. Продолжительность периода отмечена горизонтальной чертой в верхней части рисунка.

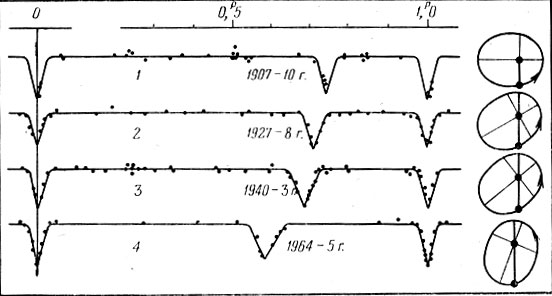
Рис. 316. Кривая изменения блеска RU Единорога и ее изменения в результате вращения линии апсид

Второй тип затменных переменных - звезды типа Р Лиры. Кривая изменения блеска этой звезды (рис. 173) обладает двумя округлыми максимальными частями, что вызвано отличием фигур компонент от шаровой. Обе компоненты вытянуты под влиянием приливных сил навстречу друг другу, т. е. имеют продолговатую форму. Первичный и вторичный минимумы имеют разную глубину.

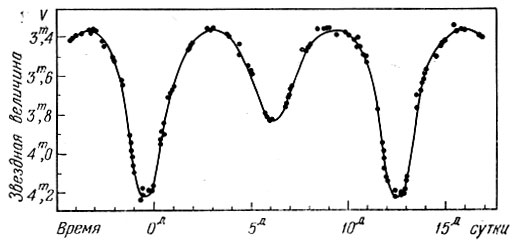
Рис. 173. Кривая изменения блеска β Лиры

Третий тип затменных переменных - звезды типа W Большой Медведицы. Это звезды, похожие на β Лиры, но имеющие короткие периоды обращения (у W Большой Медведицы период равен 0,333638 суток) и равные (или почти равные) по глубине минимумы блеска - первичный и вторичный (рис. 174). Компоненты этих двойных систем сильно вытянуты и находятся почти в соприкосновении друг с другом.

На рисунке 175 избражено распределение численности затменных звезд в зависимости от их орбитального периода. Из него мы видим, что наименьшими периодами обладают звезды типа W Большой Медвицы (W) и что их очень много. Самыми продолжительными периодами обладают звезды типа Алголя (А), и больше всего их при логарифме периода 0,1, т. е. при периоде, немного

большем суток. Гистограмма, помеченная знаком β, изображает изменение численности звезд типа Р Лиры. Она промежуточная между W и А. Мы видим, что звезд типа β Лиры гораздо меньше, чем систем типа Алголя и W Большой Медведицы.

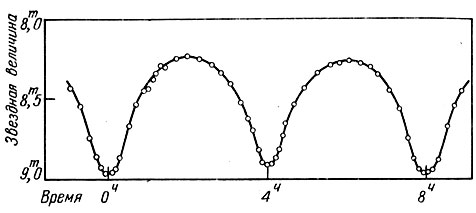
Рис. 174. Кривая изменения блеска W Большой Медведицы

Существует еще четвертый тип затменных звезд - эллипсоидальные. Это не двойные системы. Одиночная звезда, имеющая вытянутую эллипсоидальную форму, вращается вокруг оси, что приводит к небольшим изменениям размеров обращенного к наблюдателю диска звезды и вызывает очень небольшие колебания блеска. Такие звезды могут наблюдаться только с помощью очень точных фотометров. Для любительских наблюдений они интереса не представляют.

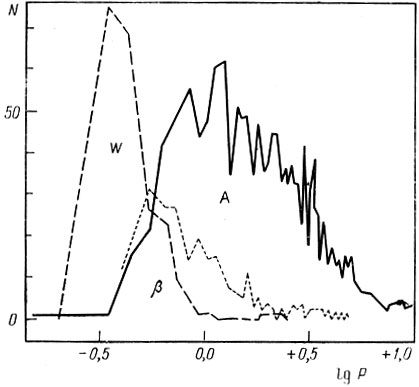
Рис. 175. Распределение численности затменных звезд различных типов в зависимости от продолжительности их периода. W - звезды типа W Большой Медведицы, β - типа β Лиры, А - типа Алголя

На первых порах предполагали, что обе компоненты затменной двойной системы обладают тонкими фотосферами, резко очерченными дисками и разделяющее их пространство не содержит вещества. Впоследствии спектральные наблюдения показали, что действительность много сложнее. Так, например, у многих затменных звезд во время полного затмения наблюдаются эмиссионные спектральные линии. Они возникают в кольцеобразной оболочке яркой звезды, вращающейся вокруг нее наподобие кольца Сатурна.

Еще более сложные движения происходят внутри двойной системы β Лиры. Исследования ее спектра показали, что обе компоненты погружены в общую газовую оболочку, которая постепенно рассеивается в пространстве. Кроме того, вблизи каждой из компонент образуются потоки газов, идущие с большими скоростями от одной компоненты к другой. Обе звезды как бы обмениваются своим веществом. Все это очень усложняет проблему устойчивых движений газовых частиц в совместном поле тяготения двух притягивающих компонент. Несмотря на трудности, эта проблема была исследована. Было изучено, как должна двигаться частица (молекула газа) в окрестностях двух притягивающих центров. Оказалось что существует критическая поверхность, называемая поверхностью Роша (рис. 176), такая, что находящаяся вне ее молекула движется вокруг обеих компонент, описывая очень сложную орбиту. Поверхность Роша состоит из двух соприкасающихся полостей очень сложной формы. Каждая из компонент находится вблизи центра своей полости Роша. Если частица расположена внутри полости Роша, то она движется вокруг «своей» компоненты, описывая вокруг нее сложную орбиту. Однако вблизи точки соприкосновения обеих полостей она может переходить из одной полости в другую. Этим и объясняется возникновение тех газовых потоков, которыми обмениваются компоненты и которые мы наблюдаем, исследуя смещения спектральных линий.

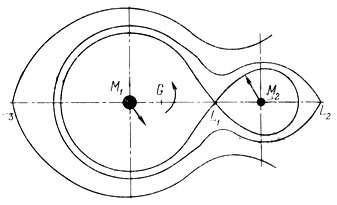
Рис. 176. Сечение поверхности Роша плоскостью орбиты тесной двойной системы. G - центр системы, М1 - массивная, М2 - менее массивная компоненты. L1 - точка соприкосновения полостей Роша

После изучения этой проблемы была создана физическая классификация тесных двойных систем. Если размеры компонент много меньше размеров соответствующих полостей Роша, то такую систему называют разделенной. Если же одна из компонент погружена в свою полость Роша, а вторая ее заполняет, то система называется полуразделенной (к такому типу систем принадлежит U Цефея). Если же обе компоненты заполняют свои полости, то система называется контактной (β Лиры, W Большой Медведицы).

Сведения о некоторых затменных звездах, которые мы рекомендуем для визуальных наблюдений, приведены в Дополнении III.