
Три модели Александра Фридмана
Знаменитые уравнения тяготения Эйнштейна представляют собой систему из десяти дифференциальных уравнений в частных производных. Грубо говоря, они показывают, как распределение масс в пространстве влияет на кривизну этого пространства. Иными словами, они показывают, как метрика пространства зависит от распределения и движения масс и как, в свою очередь, та же метрика определяет движение вещества.
Из-за чисто математических трудностей система уравнений Эйнштейна не поддавалась общему решению. Приходилось идти на различные упрощения.
Те, кто учился и работал рядом с Фридманом, часто вспоминают его любимое присловье: «А нельзя ли здесь чего-нибудь откинуть?» Не с этих ли позиций подошел он к решению уравнений Эйнштейна? Впрочем, он не откидывал лямбда-члена системы Эйнштейна, он просто решал уравнения. Оказалось что при этом возможно множество решений. Особенно интересен случай при λ=0. Решение это настолько интересно, что стоит остановиться на нем поподробнее.
В своей первой работе А. Фридман сохранил все предположения Эйнштейна, за исключением стационарности, и исследовал получившиеся нестационарные однородные изотропные модели с замкнутым пространством постоянной положительной кривизны. При этом ему удалось в отличие от Эйнштейна получить нетривиальные решения уравнений и без космологического члена. Что же представляли собой теоретические модели, полученные петроградским математиком?
Прежде всего они были нестационарны. Радиус кривизны и плотность вещества во вселенной менялись со временем. И от того, какой величины выбрать среднюю плотность, зависела судьба модели мира.
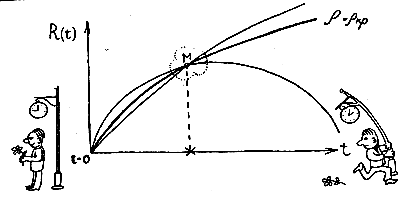
Представим себе ρ=ρкр: средняя плотность равна некоторому определенному критическому значению. Его можно вычислить по несложной формуле, воспользовавшись значениями некоторых «мировых постоянных». Но сейчас нам это не нужно. Достаточно, что такое значение существует. При критической плотности вещества пространственная часть четырехмерного мира — плоская. Однако это не неподвижная модель мира Минковского, о которой мы уже говорили. Фридмановское решение делало вселенную подвижной! Все расстояния в пространстве растут, то есть частицы разлетаются в разные стороны со скоростью, которая для малых расстояний пропорциональна приблизительно самому расстоянию.
Если для наглядности отказаться от одного измерения и перейти к двухмерному пространству, меняющемуся во времени, то такую модель можно представить себе в виде равномерно растягиваемой в разные стороны резиновой пленки. Пылинки, налипшие на ее поверхности, будут играть роль звездных систем — галактик.
Посмотрите на наш рисунок. На нем изображен график изменения расстояний в такой модели. Сухая абстрактная кривая на самом деле хранит в себе целый приключенческий роман, только в зашифрованном виде.
Начнем расшифровку с крайней левой точки нашего графика. Она убедительно говорит, что некогда все расстояния между любыми двумя точками во вселенной были пренебрежимо малыми. Не существовало ни пространства, ни времени, ни звезд, ни планет, ни туманностей... Ничего!.. Это область нулевого времени. Потом сработал некий механизм, и стало появляться вещество, частицы его стали разлетаться, начался отсчет времени, стало расширяться пространство — расстояния между любыми двумя частицами вещества стали расти со скоростью, пропорциональной самому расстоянию. Это значит, что далекие частицы разлетаются с большей скоростью, близкие — с меньшей.
Три модели Александра Фридмана
Для растягивающейся пленки такое утверждение сомнений не вызывает. Отметьте одну из пылинок на ее поверхности и представьте, что это вы — наблюдатель. Когда поверхность пленки увеличивается, то ближайшая к вам пылинка будет удаляться от вас с какой-то вполне определенной скоростью.
Более далекая покажется вам куда более шустрой. Скорость ее будет больше, чем ближайшей, и так далее.
В дальнейшем это решение использовали Эйнштейн и де Ситтер. И потому иногда эту простейшую модель называют именем этих ученых.
Но в статье Фридмана было и более «трагическое» решение. Он предположил, что средняя плотность вещества во вселенной больше критической. Прежде всего это потребовало отказа от эвклидова пространства и перехода к сферическому, риманову трехмерному пространству, да ещё с переменным радиусом кривизны.
При этом начало, то есть пресловутый «нуль-пункт», ничем не отличалось, от начала предыдущей модели.
Но дальше все шло не так. Радиус неэвклидова сферического пространства, как вы можете видеть из следующего рисунка, не увеличивался бесконечно. В точке М он достигал максимума, а потом снова уменьшался до нуля. Это означало, что в истории расширяющейся вселенной должен наступить момент, когда «разбегание» прекратится, после чего все пойдет в обратном направлении. Начнется сжатие. И через некоторое время планеты, звезды и галактики снова сольются в единый комок праматерии. Эта модель получила название закрытой.
В 1924 году из-под пера А. Фридмана вышла новая работа, посвященная теории Эйнштейна. Называлась она «О возможности мира с постоянной отрицательной кривизной». В новой работе он исследовал уравнения Эйнштейна, предположив, что плотность вещества во вселенной меньше критической. Получилась новая модель с неэвклидовой геометрией — неограниченно расширяющееся пространство отрицательной кривизны. Гиперболическое пространство Лобачевского, вызывавшее столько насмешек при жизни Великого Геометра, получило право на существование наравне с эвклидовым и римановым. Радиус пространства Лобачевского рос немного быстрее, чем в первой модели. Чтобы показать это, мы постарались выпрямить кривую третьего графика, который вы видите на предыдущей странице.
Таковы три фридмановские модели вселенной. Все они начинаются с нулевого радиуса. Все расширяются. Две из них утверждают ненулевую кривизну пространства...
Но как поверить в эти теоретические рассуждения? Как убедиться в том, что вселенная, которую человечество испокон веков видит одной и той же, на самом деле находится в состоянии непрерывного движения, расширения, разлетания... Как понять, что пусть в далеком прошлом, но существовал такой момент, когда весь мир был сжат в точку? Момент начала всего, даже нашего времени?.. Как, наконец, убедиться в том, что пространство, окружающее нас, обладает кривизной? И какую из трех моделей Фридмана принять в качестве наиболее близкой к объективной реальности?

Три модели
Эти вопросы буквально не давали спать по ночам теоретикам. Не только физики, не только астрономы и математики оказались втянутыми в дискуссию. Спор особенно обострился, когда в него вступили философы, а за ними и теологи, не желающие упустить возможности сказать и свое слово о науке с позиций религии... Вот уж поистине «куда конь с копытом, туда и рак с клешней»... И если у читателя не иссякло терпение, то автор рад ему сообщить, что последующие главы как раз и будут посвящены разрешению указанных недоумений и вопросов.
|
ПОИСК:
|
© 12APR.SU, 2010-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://12apr.su/ 'Библиотека по астрономии и космонавтике'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://12apr.su/ 'Библиотека по астрономии и космонавтике'