Приложение В. Как взвешивают звезды

Несмотря на то что современная техника подарила астрономам точнейшие измерительные устройства и позволила им применять в своих расчетах компьютеры, при определении звездных масс астрономы не продвинулись далеко от методов, восходящих еще к Иоганну Кеплеру и Исааку Ньютону, методов, которым уже триста лет. Начнем с массы Солнца. В поле силы тяжести Солнца Земля движется почти по круговой орбите. При этом она испытывает действие центробежной силы, стремящейся отбросить ее в пространство. Центробежная сила действует против притяжения Земли Солнцем - силы, которая стремится обрушить нашу планету в центр огненного солнечного шара. Земля движется точно по такой траектории, на которой эти противодействующие силы находятся в равновесии. Условие равновесия этих сил дает возможность определить силу, с которой Земля притягивается Солнцем, а следовательно, и массу последнего по формуле

(радиус орбиты планеты)³ = (гравитационная постоянная) х (масса планеты + масса Солнца) х (период обращения планеты)².

Значение гравитационной постоянной известно из физики. Радиус орбиты Земли определяется методом, описанным в приложении Б. Период обращения Земли вокруг Солнца равен одному году. Таким образом, наше уравнение содержит только одно неизвестное, сумму масс Земли и Солнца, и его нетрудно решить. Так как масса Земли ничтожна по сравнению с массой Солнца, эта сумма практически равна массе Солнца.

А как обстоит дело с массами других звезд? С двойными звездами, которые можно разделить с помощью телескопа (иначе говоря, которые наблюдаются в телескоп как звездная пара), можно поступить точно так же. Разница только в том, что здесь два тела обращаются относительно друг друга и массы их различаются не так сильно, как массы Земли и Солнца. Существенным становится то, чем мы пренебрегли в предыдущем случае: здесь не одно тело обращается вокруг другого, а каждое из них обращается вокруг их общего центра масс. Итак, для двух звезд - обозначим их А и В в двойной системе справедливо соотношение

(расстояние между двумя звездами)3 = (гравитационная постоянная) х (масса звезды А + масса звезды Б) х (период обращения)2,

а для расстояний от каждой звезды до центра масс

(расстояние от А до центра масс) х (масса А) = (расстояние от В до центра масс) х (масса В).

Естественно, расстояние от А до В равно сумме расстояний от каждой из звезд до общего центра масс (рис. В.1). Допустим, что мы смогли с помощью телескопа разделить две звезды и измерить их движение относительно общего центра масс. Тогда мы знаем расстояние между ними и период обращения и тотчас можем определить их суммарную массу. Из наблюдений мы определили также расстояние от каждой звезды до центра масс. Это дает нам отношение масс в соответствии со вторым уравнением. Зная сумму и отношение двух величин, легко определить каждую в отдельности. Все как будто очень просто; но этот метод предполагает, что мы смогли измерить не только расстояние между звездами, но и, более того, радиус орбиты каждой из них относительно общего центра масс. Наблюдая движение звезд, астроном имеет возможность измерять лишь расстояния. Чтобы определить истинные значения расстояний, нужно знать еще расстояние от нас до звезды.

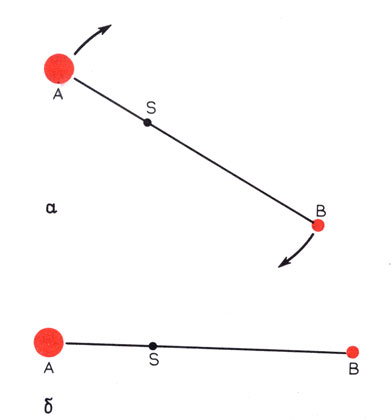
Рис. В.1. Движение простой двойной системы. Вверху: двойная система в плане. Звезды А и В движутся по окружностям разного радиуса относительно общего центра масс 5. Внизу: то же движение в плоскости системы. Когда линия, соединяющая центры звезд, оказывается перпендикулярной к направлению наблюдения, одна звезда (В) движется к наблюдателю, а другая (А) от него. Скорости движения звезд можно определить по доплеровскому сдвигу спектральных линий, как описано в приложении А.

Поскольку для определения массы по описанному методу нужно знать расстояние до двойной системы, этот прием можно применить только для относительно близких объектов. Тем не менее именно этим способом было определено соотношение между массой и светимостью звезд главной последовательности (см. рис. 2.4).

К счастью, есть и еще один способ, для которого не нужно заниматься трудоемким определением расстояния. Он основан на том, что по звездному спектру с помощью эффекта Доплера можно определить, с какой скоростью звезда движется к нам или от нас (см. приложение А). Если, как на рис. В.1, б, мы смотрим на двойную систему сбоку и в какой-то момент линия, соединяющая эти звезды, оказалась перпендикулярна направлению наблюдения, то в этот момент одна из звезд движется точно к нам, а другая от нас, и скорость каждой из них равна длине окружности ее орбиты, деленной на период обращения:

Скорость А =2 π х (расстояние от А до центра масс)/(период обращения)

Скорость В = 2 π х (расстояние от В до центра масс)/ (период обращения)

Каждая из скоростей может быть измерена с помощью эффекта Доплера, а период обращения соответствует ритму изменения скоростей. Отсюда вычисляются расстояния от каждой из звезд до центра масс, и по приведенным выше уравнениям находится масса каждой из звезд.

Самое замечательное в этом методе то, что не требуется, чтобы звезды разделялись с помощью телескопа. Даже если обе звезды видны как одна точка, по спектру можно определить, что свет исходит от двух источников, и измерить скорость каждого из них.

В действительности, конечно, все сложнее. Орбиты нередко оказываются не круговыми, а эллиптическими, и в отличие от рис. В.1 мы не смотрим на систему ни точно сверху, ни точно сбоку, а как-нибудь под углом. Но принцип описанного здесь метода остается прежним.

Поскольку для звезд главной последовательности нам известна связь между массой и светимостью, можно поступить и по-другому. Если мы знаем светимость звезды и известно, что она принадлежит к главной последовательности, то по диаграмме масса - светимость сразу можно найти массу. Для тех звезд главной последовательности, у которых можно измерить лишь температуру поверхности, из диаграммы Г - Р определяется светимость, а затем из диаграммы масса - светимость находится масса. Этот метод выручает в тех случаях, когда звезда не имеет спутника, который помог бы определить ее массу.