§ 3. О законах планетных движений

Планеты благодаря своим внешне сложным движениям сыграли решающую роль в астрономии и вообще в построении фундамента механики и физики. Еще древнегреческие астрономы поставили вопрос, не являются ли наблюдаемые сложные перемещения по небу лишь отражением более регулярных движений планет в пространстве. С этого времени начинается теоретическое построение схем планетной системы, или же, как мы говорили выше, кинематики планетных движений в пространстве.

Мы не будем останавливаться на древних схемах, основывающихся на так называемых эпициклах и эксцентрах. О них довольно много говорится в книгах по общей астрономии и в популярной литературе. Подчеркнем лишь то, что эти схемы опирались нп ложные физические принципы:

а) небесным телам свойственны только идеальные движения, какими древние ученые считали равномерные круговые движения,

б) все планеты, Солнце, Луна движутся вокруг неподвижной Земли, являющейся центром мира.

Правда, допускались комбинации круговых движений, а в таком случае, феноменологически, т. е. с точки зрения описания внешне проявляющихся эффектов в движениях планет, они были в известном смысле нравы Астрономы и в настоящее время описывают движение планет с помощью так называемых рядов Фурье. В соответствии с этим координаты планеты представляются в основном как совокупность гармонических колебаний с разными периодами и амплитудами. Каждое же гармоническое колебание можно рассматривать как результат некоторого кругового движения.

Конечно, сейчас эти ряды Фурье ищутся ил основании теоретических исследований уравнений движения небесных тел (подробнее об этом ниже). Древние же астрономы непосредственно подбирали системы окружностей, придавая им реальный физически смысл.

Вместе с тем древние астрономы старались всегда согласовать теоретические схемы и наблюдения, т. е. стихийно следовали важному методологическому принципу: критерию практики в теории познания. Как только обнаруживалось по наблюдениям, что планеты движутся не гак, как предсказывается данной схемой, то эта схема улучшалась, заменялась другой, более отвечающей наблюдениям. И в целом древние схемы неплохо описывали движение Солнца, Луны, планет, вполне удовлетворяя практическим запросам своего времени.

В период расцвета арабской астрономии (XII-XIII века) возросла точность наблюдений, было накоплено много новых данных о движениях планет, об их неправильностях. Чтобы удовлетворить этим данным, астрономы совершенствовали древние схемы, идя по пути их усложнения, добавления новых комбинаций круговых движений. Ведь геоцентрическое движение планет (наблюдаемое с Земли) слишком сложно, оно есть результат совместного движения Земли и планет, о чем астрономы тех времен не знали и его нельзя описать простой схемой. В результате получалась громоздкая система, реальность которой вызывала сомнения. Испанский король Альфонс X по этому поводу сказал: «Если бы при сотворении мира создатель спросил моего совета, то я предложил бы ему более простой план устройства Вселенной».

В природе же, как мы знаем, господствует удивительная простота. Принцип простоты законов природы принимался философами и учеными с давних пор.

Дальнейшее развитие астрономии проиллюстрировало ту истину, что теории, основанные на ложных принципах, хотя и могут достичь определенного, а иногда внешне достаточно высокого уровня совершенства, но все же торжествуют лишь временно, и не могут полностью отразить природу. Они в конце концов отбрасываются вместе со своими ложными принципами.

Качественно новый шаг был сделан великим польским астрономом Николаем Коперником. Он отказался от принципа геоцентризма, т. е. от неподвижной Земли как центра мира, и построил гелиоцентрическую систему мира, в которой неподвижным является Солнце, а все планеты, в том числе Земля, движутся вокруг Солнца. Планеты были поставлены, как говорится, на свои истинные места в Солнечной системе. Коперник, выдвинув правильный принцип, оказал решающее влияние на все последующее развитие естествознания и заслужил признание, как один из величайших реформаторов науки.

Другой ложный принцип - равномерных круговых движений - Коперник преодолеть не сумел. Движение каждой планеты вокруг Солнца он представлял как комбинацию таких движений.

Один из первых коперниканцев, немецкий математик и астроном Эразм Рейнгольд (1511-1553) составил в 1551 году, основываясь на гелиоцентрической системе Коперника, таблицы движения планет, названные им «Прусские таблицы» (так как они были изданы на деньги герцога Альберта Прусского) (Таблицы движения планет - это таблицы, где приводятся положения (координаты) планет, предсказываемые, т. е. вычисляемые в соответствии с той или иной теорией на определенным период времени, причем обязательно обычно на ряд лет вперед. Такие таблицы составлялись астрономами с тех пор, как появились первые теории движения планет. Точность таблиц оценивается тем, насколько близки наблюдаемые и предсказываемые положения той или иной планеты Эти таблицы, как и всякие другие таблицы положений небесных светил (в настоящее время издаются Астрономические ежегодники), предназначались для использования в навигации, в наблюдениях на астрономических обсерваториях, в предсказании солнечных и лунных затмений, а также других небесных явлений)). Эти таблицы оказались более точными, чем все предыдущие, основанные на старых схемах и это очень способствовало укреплению идеи гелиоцентризма, с огромным трудом пробивающей путь сквозь устоявшиеся веками и привычные для тех времен взгляды, а также преодолевающей реакционное идеологическое давление церкви.

В отношении точности таблиц Рейн гольда можно привести следующий пример.

В 1563 году наблюдалось тесное видимое сближение Юпитера и Сатурна. Прусские таблицы «ошиблись» в предсказании этого явления на несколько дней (это соответствовало ошибке в координатах планет около 10'). Предшествующие же таблицы «ошибались» на целый месяц, т. е. примерно на 2°.

Принцип равномерных круговых движений был отброшен другим великим астрономом - Иоганном Кеплером (1571-1630).

В 1609 году увидела свет изданная в Праге книга Кеплера, известная сейчас под названием «Новая астрономия». (Полное ее название в переводе на русский язык: «Новая астрономия, причинно обоснованная, или физика неба, изложенная в исследованиях движения звезды Марс, по наблюдениям благороднейшего мужа Тихо Браге».)

Эту книгу можно поставить в один ряд со значительнейшими научными грудами всех времен. Здесь были изложены знаменитые законы движения планет, получившие в астрономии название первых двух законов Кеплера и обессмертившие имя их автора.

Первый закон. Каждая планета движется в пространстве по эллипсу, причем Солнце находится в одном из фокусов итого эллипса.

Второй закон. Радиус-вектор планеты (т. е. отрезок, соединяющий Солнце и планету) описывает равные площади в равные промежутки времени. Этот закон часто называют законом площадей (рис. 5).

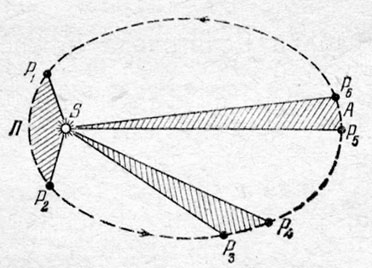
Рис. 5. Иллюстрация ко второму закону Кеплера. Заштрихованные области имеют равную площадь

Так как эллипс - плоская фигура, то первый закон подразумевает, что каждая планета движется, оставаясь все время в одной и той же плоскости.

Эти законы замечательны своей лаконичностью н простотой. Они заменяют все прежние сложные схемы, основанные на комбинациях круговых движений и представляют в целом истинную геометрическую (кинематическую) кьртину движения планет.

Второй закон указывает прежде всего на изменение скорости движения планеты по ее орбите: чем ближе планета подходит к Солнцу, тем быстрее она движется. Но он дает на самом деле больше. Он целиком определяет движение планеты по ее эллиптической орбите.

Мы не будем останавливаться подробно на истории замечательных открытий Кеплера, по хотим все же отметить следующее.

1. Отправным пунктом для Кеплера служило сравнение теории и наблюдений. Дело в том, что к концу XVI века Прусские таблицы, составленные, как мы говорили выше, по теории Коперника, стали предсказывать движение планет очень неточно. Наблюденные и вычисленные по этим таблицам положения планет отличались на 4-5°, что было недопустимо в астрономической практике. Отсюда вытекало, что планетная теория Коперника нуждается в исправлении.

2. Чтобы осуществить такое исправление, Keплер имел в своем распоряжении ценнейший наблюдательный материал - многочисленные записи наблюдений планет, выполненные одним из искуснейших астрономов-наблюдателей всех времен Тихо Браге (1546-1601). Кеплер выбрал для анализа планету Марс, так как ее наблюдаемое движение выглядело наиболее сложным, а таблицы предсказывали его хуже всего.

3. В начале Кеплер пошел по пути уточнения и усложнения схемы Коперника. Конечно, он был глубоко убежден в истинности принципа гелиоцентризма и стал подбирать новые комбинации окружностей (эпициклов, эксцентров). Ему удалось подобрать в конце концов такую комбинацию, что его схема давала ошибку по сравнению с наблюдениями до 8'. Но Кеплер был уверен, что Тихо Браге в своих наблюдениях не мог допускать таких ошибок (действительно, ич точность, как было установлено позже, составляла около 2') (Изменение положений светил на небе в 4' остается почти незаметным для невооруженного глаза человека со средней силой зрения. Тихо Браге добился большой точности, используя очень хорошие но тем временам астрономические инструменты, хотя не лишенные оптики, но снабженные различными механическими приспособлениями, облегчающими точное фиксирование направления на то или иное небесное светило)).

Поэтому Кеплер заключил, что «виновата» теория, поскольку она не согласуется с астрономической практикой. Он отбросил полностью схему, основанную на эпициклах и эксцентрах, и стал искать другие схемы. Результатом и явилось открытие для Марса первых двух законов.

Кеплер верил, что эти законы должны быть общими для всех планет и сформулировал их в общем виде для всей Солнечной системы.

Эти первые два закона характеризуют движение вокруг Солнца каждой планеты, рассматриваемой отдельно. Но Кеплер интуитивно чувствовал, что существуют закономерности, связывающие всю планетную систему в целом. И он ищет эти закономерности в течение десяти лет, прошедших после публикации «Новой астрономии». Богатейшая фантазия и огромное усердие привели Кеплера к его так называемому третьему закону, который, как и первые два, играет важнейшую роль в астрономии.

Этот закон гласит:

Квадраты периодов обращения двух планет вокруг Солнца пропорциональны кубам их средних расстояний от Солнца.

Математически этот закон выражается так:

Пусть Т₁ и Т₂ - периоды обращения двух планет вокруг Солнца и а₁, а₂ - их средние расстояния от Солнца соответственно. Тогда справедлива пропорция

(Т²₁/T²₂)=(a³₁/a³₂). (3)

Здесь же приведем формулы, являющиеся математическим выражением первых двух законов Кеплера.

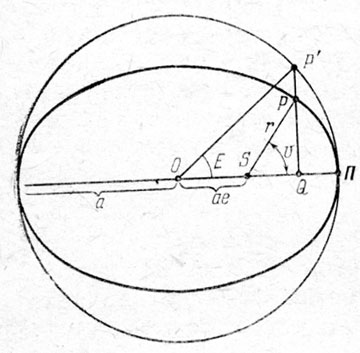
Рис. 6. Гелиоцентрическая орбита планеты Р. S - Солнце, r, υ - полярные координаты планеты, П - перигелий орбиты, Е - эксцентрическая аномалия, <PQS=π/2

На рис. 6 представлена эллиптическая орбита планеты. Здесь 5 - Солнце, Р - положение планеты в некоторый момент t. Пусть а - большая полуось эллипса, е - эксцентриситет. II - перигелий орбиты (ближайшая точка к Солнцу), Т - период обращения планеты, a t₀ - момент, когда планета проходит через перигелии. Величина n=360°/T называется средним угловым движением планеты вокруг Солнца, а угол φ=n(t-t₀) - средней аномалией. Расстояние r от Солнца до планеты (радиус-вектор) в момент t угол υ (он называется истинной аномалией) между r и направлением на перигелий П выражаются с точностью до третьих степеней эксцентриситета (т. е. в точных формулах имеются еще члены с е⁴, е⁵ и т. д.) следующим образом:

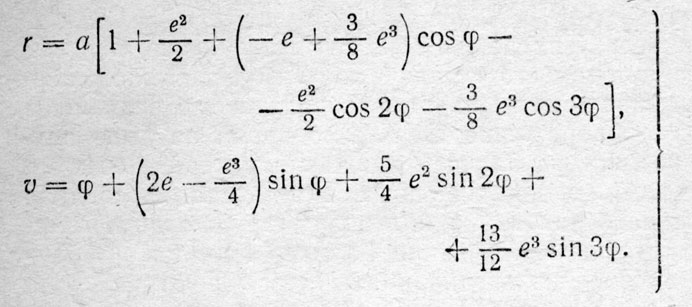
(4)

Законы Кеплера замечательны и тем, что они, если можно так выразиться, более точны, чем сама действительность. Они представляют собой точные математические законы движения для идеализированной «Солнечной сптемы», в которой планеты - материальные точки бесконечно малой массы по сравнению с «Солнцем». В действительности же планеты имеют ощутимую массу, так что в фактическом их движении имеются отклонения от законов Кеплера. Такая ситуация имеет место в случае многих известных сейчас физических законов. Эти законы сформулированы и справедливы для идеальных жидкостей, идеальных газов или тому подобное, так что фактически в природе они никогда не выполняются абсолютно точно. Но эти законы позволяют выделить главные, наиболее существенные связи в явлениях природы (разумеется, на соответствующем уровне изучения этих явлений).

На уровне точности наблюдений видимых положений планет, характерном для XVII века, законы Кеплера целиком отражали наиболее главные и существенные особенности движений в планетной системе, если их рассматривать только с точки зрения геометрии, кинематики.

В 1627 году Кеплер издал Рудольфинскне таблицы (названные в честь его покровителя - немецкого императора Рудольфа). Эти таблицы позволяли вычислять положение планет в соответствии с его законами, а также данные о некоторых астрономических явлениях, например, о затмениях. Они превосходили по точности Прусские и все предыдущие таблицы. Астрономы пользовались этими таблицами более 100 лет.

Законы Кеплера, как мы отмечали выше, являются результатом его титанического труда, помноженного на гениальность их открывателя и его редчайшее научное воображение. Ведь в то время не было науки динамики, изучающей движение материальных тел под действием приложенных к ним сил. Последняя оформилась как наука благодаря трудам двух гениальных ученых: итальянца Галилео Галилея (1564-1642) и особенно англичанина Исаака Ньютона.

После открытия Ньютоном закона всемирного тяготения (гласящего, что если имеется система двух материальных точек, то сила их взаимного притяжения пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними) и трех законов динамики, известных в литературе как законы Ньютона, выяснилось, что законы планетных движений являются следствиями законов ньютоновой динамики.

Поясним это утверждение.

Рассмотрим механическую систему, состоящую из двух материальных точек 5 и Р с массами М и т соответственно. Предположим также, что масса М во много раз превышает массу (М>>m). Именно такая ситуация встречается в Солнечной системе, где масса Солнца более чем в 1000 раз превышает массу самой большой планеты - Юпитера. В механике такой вариант задачи двух тел часто называется планетным вариантом, в отличие от звездного варианта задачи двух тел (здесь массы предполагаются примерно равными или отличными одна от другой в несколько раз).

Из уравнений механики Ньютона вытекает, что движение каждого из двух тел вокруг общего центра масс происходит по эллипсу, параболе или гиперболе. Других орбит в задаче двух тел быть не может и движение тела по одной из трех перечисленных траекторий целиком определяется величинами скорости и расстояния в некоторый начальный момент времени.

Пусть в начальный момент времени расстояние между точками S и Р равно r₀, а скорость точки Р равна V₀ и направлена перпендикулярно к r₀ (рис.7). Из законов Ньютона следует, что траектория точки Р является плоской кривой, лежащей в плоскости SPV₀ - Если квадрат начальной скорости V²₀ непревышает величины 2f(M+m)/r₀ (f - постоянная тяготения), то орбита точки Р является эллипсом. В частности, если V²₀=f(M+m)/r₀, то орбита планеты Р представляет собой окружность. Такая скорость называется круговой.

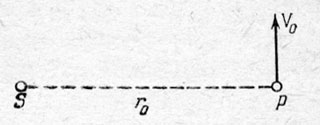
Рис. 7. Взаимное расположение Солнца S и планеты P в момент прохождения планеты через перигелий

Если V²₀=2f(M+m)/r₀, то орбита точки Р перестает быть замкнутой кривой и становится параболой. Двигаясь по параболе, точка Р за бесконечный отрезок времени удалится от S на бесконечное расстояние и никогда не возвратится в ее конечную окрестность. При V²₀>2f(M+m)/r₀ точка Р будет двигаться также по незамкнутой кривой, но гиперболе, с той лишь разницей, что она еще быстрее будет удаляться от S.

Ньютон в своем знаменитом сочинении «Математические начала натуральной философии» доказал, что движение по эллиптической орбите в задаче двух тел происходит в соответствии с законами Кеплера, а его второму закону можно придать и красивый механический смысл. Оказывается, что он выражает постоянство момента количества движения механической системы как по величине, так и по направлению. Более того, из закона всемирного тяготения как следствие вытекает уточненный третий закон Кеплера. Вместо приближенной формулы (3) следует писать точное равенство:

(T²₁(M+m1))/(T²₂(M+m₂))=(a³₁)/(a³₂). (5)

В формуле (5) Т₁, T₂, а₁, a₂, как и раньше, - периоды обращения двух плане г вокруг Солнца и их средние гелиоцентрические расстояния, m₁, m₂ - их массы, М - масса Солнца.

Сейчас именно соотношение (5) принято называть третьим законом Кеплера. Он играет ключевую роль при определении масс планет и спутников. Действительно, периоды обращения планет вокруг Солнца и их гелиоцентрические расстояния определяются с помощью специальных математических методов обработки наблюдений, а массы планет непосредственно из наблюдений невозможно получить. В нашем распоряжении нет грандиозных космических весов, на одну чашу которых мы положили бы Солнце, а на другую - планеты. Третий закон Кеплера и компенсирует отсутствие таких космических весов, так как с его помощью мы легко можем определить массы небесных тел, образующих единую систему. Например, если считать, что T₁, T₂, a₁, a₂, M, m₁ - известные величины, то тогда равенство (5) становится уравнением относительно неизвестной величины m₂ и его решение - элементарное дело.

Но законы Кеплера точно описывают движение планеты в рамках задачи двух тел, а наша Солнечная система является многопланетной системой, поэтому для нее эти законы являются лишь приближенными. Парадоксальным является к тому же тот факт, что именно для Марса, наблюдения которого и привели к их открытию, законы Кеплера выполняются менее точно. Марс, как и все члены Солнечной системы, притягивается не только Солнцем, но и другими планетами, и в особенности самой большой планетой, Юпитером, которые ежесекундно отклоняют Марс от эллиптической орбиты. В подобной ситуации находится каждая планета, но Марс ближе других подходит к Юпитеру (минимальное расстояние между ними - 3,5 а. е.), поэтому он испытывает наибольшие возмущения. Взаимные планетные возмущения обусловливают то, что реальные орбиты планет - сложные пространственные кривые, для описания которых нет простых аналитических формул, однако эти кривые обладают тем замечательным свойством, что на одном, двух оборотах хорошо представляются эллипсами.