§4. ЗВЕЗДЫ

Космический взрыв заключается в быстром изменении состояния какого-либо небесного тела. Следовательно, перед тем как рассматривать различные виды космических взрывов, необходимо получить отчетливое представление о формах вещества и энергии, присущих различным телам. Выяснение вопросов, относящихся к разным видам энергии, мы отложим, а в этом и следующем параграфах кратко охарактеризуем строение небесных тел, т. е. опишем состояния, в которых находится вещество в доступной нашим наблюдениям области Вселенной.

Взрывы могут происходить на любых небесных телах, включая Луну и планеты Солнечной системы. Но в этой книге мы не будем говорить о взрывах на планетах и их спутниках, так как по своей природе они, вероятно, гораздо ближе к земным взрывам (извержениям вулканов, землетрясениям), чем к звездным. Поэтому мы не будем останавливаться и на описании Солнечной системы, тем более, что ее строение широко известно по многочисленным популярным книгам.

Как показывают наблюдения, Вселенная является в основном звездной, т. е. преобладающая часть имеющегося в ней вещества сосредоточена в звездах. Естественно, что мы больше внимания уделим звездам, а также и Солнцу. Хотя Солнце является самой обычной звездой, но благодаря ее особому положению (сравнительной близости к земным наблюдателям) о ней известно гораздо больше, чем о других звездах.

Знакомясь с любыми космическими явлениями, полезно возможно скорее привыкнуть к масштабам звездного мира, т. е. к расстояниям, отделяющим нас от звезд, к размерам звезд и звездных систем. Эти масштабы сильно отличаются от земных, и для определения расстояний в Космосе применяются свои, особые методы.

В исторически первом и до последнего времени главном способе определения расстояний до тел Солнечной системы и ближайших звезд используется явление так называемого параллактического смещения. Как хорошо известно, при перемещении наблюдателя предмет, близкий к нему, кажется смещающимся относительно более далеких предметов, составляющих фон. Величина этого кажущегося параллактического смещения предмета зависит как от того, насколько переместился наблюдатель, так и от расстояния между ним и предметом. Параллактическое смещение при одинаковом сдвиге наблюдателя тем меньше, чем дальше находится предмет.

Расстояния от Земли до тел Солнечной системы ничтожно малы по сравнению с расстояниями до звезд. При перемещении наблюдателя по земной поверхности направление на звезду практически не меняется. Но для двух наблюдателей, видящих, например, Луну из разных точек Земли в один и тот же момент, направление на нее будет различным и соответствующее смещение Луны заметно на фоне звезд. Расстояние между наблюдателями, так же как видимое угловое смещение Луны (при переходе от одного наблюдателя к другому), нетрудно измерить и затем получить расстояние от Земли до Луны, Оно оказывается равным в среднем 384 000 км (Так как Луна движется не по окружности, то ее расстояние от Земли неодинаково в разные моменты.). На этом расстоянии радиус Земли укладывается шестьдесят с лишним раз. Аналогичным способом определено и расстояние от Земли до Солнца. Оно составляет около 150 миллионов километров.

Как мы уже сказали, перемещение по земной поверхности практически не влияет на видимое положение звезд. Однако перемещение наблюдателя вместе с Землей при ее движении вокруг Солнца за полгода на 300 миллионов километров уже сказывается на видимом положении близких звезд относительно более далеких. Эти изменения очень малы - меньше одной секунды дуги, но, применяя очень точные астрономические инструменты, их определяют вполне уверенно, если они больше 0,01. Из таких измерений нашли, что даже ближайшие к нам звезды находятся в сотни тысяч раз дальше, чем Солнце. Чтобы преодолеть это расстояние, фотону, летящему со скоростью 300 000 км/сек, требуется несколько лет. Таков порядок расстояний между звездами. Для измерения столь больших расстояний в астрономии пользуются двумя единицами: световым годом и парсеком; 1 световой год равен 9,5 х 10¹⁷ см, 1 парсек (пс) равен 3,26 светового года. Расстояние до ближайшей к Солнцу звезды (а из созвездия Центавра) составляет 4,3 светового года.

На таких огромных расстояниях диски звезд увидеть нельзя. Даже при наблюдениях с помощью самых больших телескопов все звезды представляются точечными источниками света. Для определения размеров всех, за исключением Солнца, звезд приходится применять косвенные методы, основанные на определении их температур. А температуры, как мы уже говорили, можно находить по спектру идущего от светила излучения.

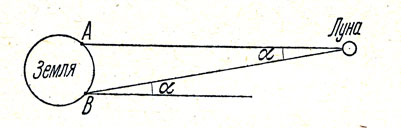
Рис. 11. Определение расстояния до Луны. Непосредственно измеряется угол а и дуга А В на земной поверхности.

Спектры почти всех звезд содержат множество линий поглощения. Из этого заключают, что внешние слои звезды, ее атмосфера, состоят из разреженного газа. Тот фон, на котором видны линии поглощения - непрерывное излучение - возникает на более глубоком уровне, в слоях, называемых фотосферой звезды.

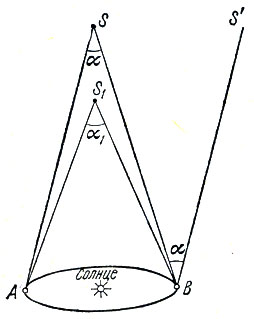
Рис. 12. Параллактическое смещение звезд вследствие орбитального движения Земли вокруг Солнца.

Путем анализа линий поглощения в спектре Солнца нашли, что температура газа, составляющего атмосферу Солнца, близка к 4700 9К. У большинства других звезд температура в атмосфере отличается от этого значения не более чем в 2-3 раза, хотя существуют и очень горячие звезды с температурами порядка 100 000 °К. В зависимости от того, линии каких элементов преобладают в спектре звезды, ее относят к тому или иному спектральному классу. Спектральный класс звезды определяется значениями температуры и давления в ее атмосфере. В табл. 1 приводятся обозначения спектральных классов буквами латинского алфавита (эти обозначения сложились исторически и порядку букв не следует придавать особенного смысла). Там же указываются элементы, спектральные линии которых наиболее характерны для данного класса, а также средние для класса температуры, находимые по этим линиям. На детализации этой классификации мы не останавливаемся. Заметим, что Солнце относится к классу G.

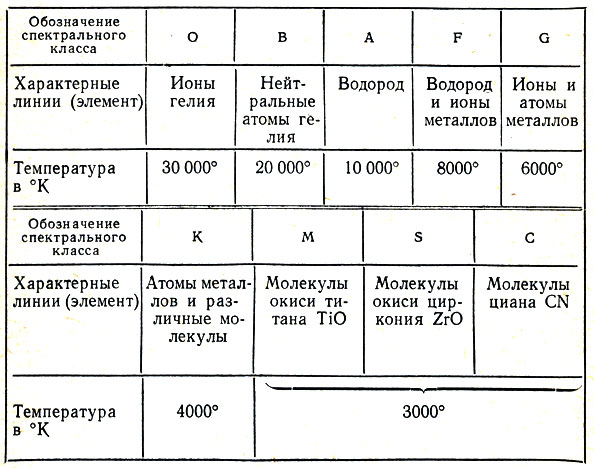
Таблица 1. Обозначение спектрального класса звезды

При существующих в атмосферах звезд условиях вещество не может находиться ни в каком другом состоянии, кроме газообразного. При этом газ атомарный и лишь у самых холодных звезд (их называют звездами поздних классов) атмосферы содержат молекулы, представляющие собой соединение двух или большего числа атомов. При температурах, превосходящих 4000°, даже самые устойчивые молекулы распадаются (диссоциируют). Помимо химических соединений, указанных в таблице, в атмосферах холодных звезд имеются и другие, но эти наиболее заметно себя проявляют в поглощении света.

По спектрам звезд находят и химический состав звездных атмосфер. Они сильно отличаются от земной атмосферы по относительному содержанию различных элементов. Почти во всех звездах наиболее распространенным элементом оказывается водород, составляющий около 60% всей массы газа. Следующим по массе является гелий, а на все более тяжелые элементы - кислород, азот, углерод, металлы - приходится лишь 1-2% от общего количества газа. Только у очень небольшого числа звезд наблюдается повышенное содержание тяжелых элементов и сравнительно малое содержание водорода.

Физические условия в атмосферах звезд характеризуются не только высокой температурой, но и очень малой плотностью вещества. Число частиц в 1 см³ газа, составляющего солнечную атмосферу, порядка 10¹⁴, что в сотни тысяч раз меньше, чем число частиц в таком же объеме воздуха у поверхности Земли. При температурах в тысячи и десятки тысяч градусов газ плохо пропускает излучение с длинами волн оптического диапазона. Слой, содержащий всего несколько граммов газа на 1 см² площади, непрозрачен даже для излучения в непрерывном спектре. Увидеть, что происходит в звезде глубже этого слоя, нельзя - луч света непосредственно оттуда не доходит до наблюдателя. Следовательно, количество вещества в доступных для наблюдения областях звезды весьма мало, в расчете на 1 см² ее поверхности, по сравнению с соответствующим количеством земной атмосферы. Напомним, что на 1 см² поверхности Земли приходится более 1 кг воздуха.

В звезде нет резкой границы между атмосферой и более глубокими слоями. По мере углубления в звезду плотность газа возрастает. Так как непрозрачность газа очень быстро увеличивается с ростом плотности и температуры, толщина атмосферы составляет очень малую долю размера звезды. За поверхность звезды принимается, грубо говоря, тот уровень, глубже которого ничего не видно. Расстояние этого уровня от центра и считается радиусом звезды. При определении радиусов звезд по их излучению основываются на общих законах излучения, к которым мы и перейдем.

Из повседневного опыта хорошо известно, что чем сильнее нагрето тело, тем больше энергии оно излучает. Этот факт имеет место как для твердых тел, так и для газа. Однако излучательная способность различных тел не одинакова. Эксперименты показали, что она связана со способностью тела поглощать попадающее на него излучение. Лучше всего поглощают свет тела черного цвета. Идеальное тело, которое могло бы поглощать все падающее на него электромагнитное излучение, называют абсолютно черным телом. Все реальные природные тела отражают некоторую долю падающей на них энергии и поэтому могут лишь в той или иной степени приближаться по своей поглощательной способности к абсолютно черному телу. Например, сравнительно хорошо воспроизводит свойства такого тела металлический шар, окрашенный в черный цвет.

Для абсолютно черного тела имеет место зависимость между его температурой и количеством энергии, излучаемой с единицы поверхности. Опытным путем было обнаружено и затем доказано теоретически, что энергия E, излучаемая с единицы поверхности абсолютно черного тела за единицу времени, должна быть пропорциональной четвертой степени его абсолютной температуры Т:

Е = σТ⁴.(6)

Коэффициент пропорциональности а в этом соотношении, называемом законом Стефана - Больцмана, в системе единиц CGSE равен 5,7 х 10^-5 эрг/град⁴ х сек х см².

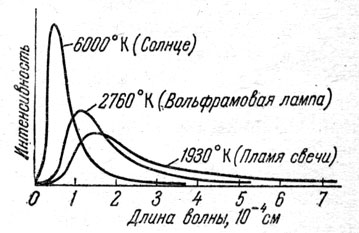
Рис. 13. Распределение энергии в спектре абсолютно черного тела при различных температурах.

Излучение абсолютно черного тела обладает еще одним важным свойством. Зависимость количества излучаемой энергии от длины волны излучения (т. е. спектр излучения) полностью определяется значением температуры тела. Чтобы не усложнять изложения, мы не будем приводить формулу, выражающую эту зависимость, и ограничимся графическим представлением спектра абсолютно черного тела при различных значениях температуры (рис. 13). Как видно из этого рисунка, чем выше температура, тем меньше длина волны λ_max, соответствующая максимальному количеству излучаемой энергии (в единичном промежутке длин волн). Точное выражение зависимости λ_max между и Т, называемой законом Вина, имеет вид

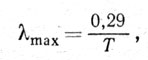
если λ_mах выражать в сантиметрах, а Т в °К (7)

Основной вклад в излучение вносит та область длин волн, которая близка к λ_mах. Это излучение определяет цвет тела. Таким образом, из закона Вина можно найти, как при изменении температуры излучающего тела должен меняться его цвет. Так, например, при Т=4500° значение λmaх= = 6,5 х 10^-5см, что соответствует излучению красного цвета. При температуре, близкой к 6000°, имеем λmax ≈5,0 х 10^-5 см. Излучение в этой длине волны желтого цвета.

Ни одна из звезд не обладает полностью свойствами абсолютно черного тела. Но, поскольку вещество фотосферы хорошо поглощает излучение, считают, что излучение фотосферы близко к излучению абсолютно черного тела. Это предположение является довольно грубым, так как наблюдатель воспринимает одновременно излучение различных слоев звезды. При углублении в звезду температура повышается. В тех слоях, где образуются линии поглощения, т. е. в атмосфере звезды, температура ниже, чем в фотосфере, являющейся основным источником излучения в непрерывном спектре. Кроме того, в разных длинах волн прозрачность фотосферы неодинакова, поэтому излучение в этих частотах соответствует различным температурам. Тем не менее, предположение о том, что звезды являются идеальными излучателями, не приводит обычно к значительным ошибкам в их радиусах, находимых по излучению.

Общее количество энергии, излучаемой звездой за 1 сек, называется светимостью звезды. Ее принято обозначать буквой L. Считая, что звезда, радиус которой равен R_*, излучает как абсолютно черное тело с температурой Т, светимость получим, умножив энергию Е, определяемую соотношением (6), на площадь поверхности звезды:

L = 4πR_*²σТ⁴ (8)

Для нахождения радиуса из формулы (8) нужно, помимо температуры, знать и светимость звезды. Она определяется по тому количеству энергии, которое достигает наблюдателя, при известном расстоянии до звезды.

Найдем, для примера, светимость Солнца; она укажет нам порядок этой величины, характерный для многих звезд. Непосредственными измерениями получено, что за 1 сек на 1 см² поверхности Земли попадает от Солнца 1,4 х 10⁶ эрг энергии. Эта величина называется солнечной постоянной. Но столько же энергии должно падать за 1 сек на любую площадку площадью в 1 см², если она удалена от Солнца так же, как и Земля, и расположена перпендикулярно к солнечным лучам. Следовательно, общее количество энергии, излучаемой Солнцем за 1 сек, находится путем умножения солнечной постоянной на площадь сферы, радиус которой равен расстоянию от Земли до Солнца. Светимость Солнца L (знаком обозначают величины, относящиеся к Солнцу) равна: 4π(1,5 х 10¹³)² х 1,4 х 10⁶=3,9 х 10³³ эрг/сек.

Найдем теперь по формуле (8) величину R. В качестве T примем приближенное значение 6000°, которое находится из закона Вина: мы знаем, что Солнце желтого цвета, а, как отмечалось выше, такой цвет имеет тело с температурой 6000°. Это значение относится к фотосфере Солнца. То же самое значение температуры фотосферы Солнца получается, если определять ее по наклону кривой, характеризующей зависимость излучаемой в непрерывном спектре энергии от длины волны излучения. Используя формулу (8), имеем: R≈700000 км. Так как видимый радиус Солнца в угловой мере и расстояние до Солнца известны, то R находится и независимо от сделанных предположений. Оказывается, что найденное нами значение R очень близко к наблюдаемому.

Для других звезд применение формулы (8) дает единственный способ определения их размеров (если не касаться сравнительно малого числа звезд, находящихся в фотометрических двойных системах; о них будет сказано позже). Значение температуры звезды, входящее в (8), оценивается по ее излучению в непрерывном спектре и называется эффективной температурой. Температура, определяемая по линиям поглощения и соответствующая атмосфере звезды, приблизительно на 15-20% ниже эффективной температуры. Для Солнца значение эффективной температуры равно 5800°, а температура возбуждения 4700°.

При определении светимости звезды по количеству принимаемой от нее энергии излучения эта звезда сравнивается с каким-либо из тех источников, для которых излучаемая энергия известна, например с Солнцем. При этом учитывается, что поток энергии изменяется обратно пропорционально квадрату расстояния от источника излучения (см. § 2). Расстояния до ближайших звезд, удаленных от Солнца не более чем на 100 световых лет, определяются по их параллактическим смещениям. Для других звезд эти смещения настолько малы, что их не удается измерить, а значит, нельзя узнать расстояния, необходимые для определения светимостей. В таких случаях используются более сложные способы непосредственного определения светимостей звезд. В основе их лежит полученная путем исследования ближайших звезд зависимость между величиной светимости звезды данного спектрального класса и рядом особенностей в линиях поглощения ее спектра.

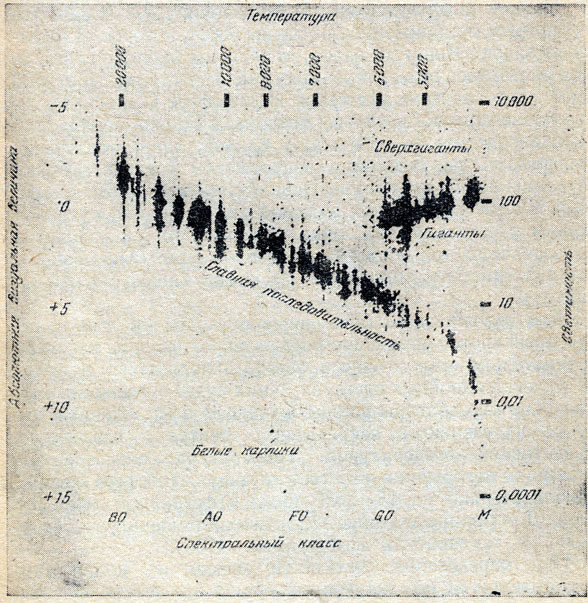
Рис. 14. Диаграмма спектр - светимость.

Спектры же можно получать и для очень далеких звезд. Для них сначала по спектру находят светимости, а затем по светимостям можно определить и расстояния.

По светимостям звезды сильно различаются друг от друга. Солнце относится к звездам относительно малой светимости. Звезды подобные Солнцу и более слабые, излучающие энергию порядка 1033 эрг/сек или меньше, называют карликами. Самые слабые карлики обладают светимостью в тысячи раз меньшей, чем у Солнца. Наряду с этим существуют звезды, называемые гигантами и сверхгигантами, превосходящие Солнце по светимости в сотни и тысячи раз.

Между светимостями и температурами звезд обнаружена зависимость. Если для каждой звезды определить светимость, скажем, в единицах L, и спектральный класс, характеризующий температуру, а затем нанести соответствующие точки на график, то получится диаграмма, подобная изображенной на рис. 14. (Впервые такая диаграмма была построена астрофизиками Герцшпрунгом и Ресселом.) Подавляющее большинство звезд попадает в область так называемой главной последовательности. Для них, как мы видим, светимость, радиус и температура связаны не только соотношением (8). Температурой определяется светимость, правда, не вполне точно: можно указать некоторый сравнительно узкий промежуток возможных значений светимости, соответствующих данной температуре.

В правой верхней части диаграммы выделяется группа звезд - гигантов и сверхгигантов. Их мало по сравнению со звездами типа Солнца, но они благодаря своей высокой светимости заметны на гораздо больших расстояниях, чем карлики. Поэтому создается впечатление многочисленности гигантов и сверхгигантов.

Радиусы звезд лежат в очень широких пределах. У карликов, относящихся, как видно из диаграммы, к спектральным классам G, К и М, они порядка 0,1Rо - 1Rо. Гиганты и сверхгиганты ранних спектральных классов О, В, А - имеют радиусы порядка 5R - 10R. Температуры гигантских звезд классов К и М низки и их большая светимость связана с огромными размерами поверхности. Радиусы у них в сотни раз превосходят солнечный.

Среди звезд часто встречаются (приблизительно одна звезда из каждых десяти) особенные, с очень малыми радиусами. Их называют белыми карликами. Температура белого карлика больше, чем у Солнца (поэтому цвет его излучения голубой или белый), а светимость, как видно из диаграммы спектр - светимость (рис. 14), в сотни раз меньше. Поэтому белые карлики очень малы по сравнению с Солнцем. При помощи формулы (8) нетрудно подсчитать, что белый карлик с температурой, вдвое превосходящей солнечную, и.светимостью, равной одной сотой светимости Солнца, имеет радиус в сорок раз меньший, чем радиус Солнца.

Наряду с радиусом и светимостью одной из важнейших характеристик звезды является ее масса. У небеснйх тел массы можно находить только по создаваемому ими тяготению. Начнем с определения массы Солнца. Она находится по тому действию, которое Солнце оказывает на соседние тела, в частности на Землю. Это действие определяется законом всемирного тяготения Ньютона:

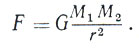
Он выражает величину силы притяжения F, действующей на тело с массой М₁, со стороны тела с массой М₂ при расстоянии между телами, равном r. Коэффициент пропорциональности G называется постоянной тяготения. В том случае, когда M₁, M₂, r и F выражены в системе единиц CGSE, величина G = 6,67 х 10^-8 см³ х сек^-2 х г^-1. Она определена путем измерения в лаборатории силы взаимодействия двух тел с известными массами. Так как это взаимодействие очень слабое, такой опыт, принципиально простой, является технически весьма сложным.

Если относительная скорость двух тел, притягивающихся друг к другу по закону Ньютона, достаточно мала, то они движутся вокруг общего центра тяжести. Квадрат периода обращения Р пропорционален кубу среднего расстояния между ними:

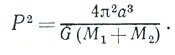
Положив M₂=M, а за M₁ приняв массу какой-либо планеты, получаем из (10) один из законов движения планет вокруг Солнца, установленных Кеплером в XVII в. из наблюдений, еще до открытия Ньютоном закона всемирного тяготения (Выражение закона Кеплера в его первоначальной форме не содержало массы планеты, но так как эта масса всегда гораздо меньше солнечной, то заметной ошибки не получалось.). Применим формулу (10) к системе Солнце - Земля, пренебрегая действием других планет. Период обращения для Земли, как известно, называется годом и содержит 60 х 60 х 24 х 365 1/4 сек. Используя это значение Р и величину среднего расстояния от Земли до Солнца а= 150000000 км, получаем, что М+ М_земли=2 х 10³³ г.

Так как масса Земли (находимая по известной величине ускорения силы тяжести g на земной поверхности) равна всего 6 х 10²⁷ г, то, следовательно, для М имеем значение 2 10³³ г, что в 330 000 раз превосходит массу Земли.

Мы получили представление о том, каков порядок величины массы звезды. Аналогичным путем по соотношению (10) находят массы других звезд, входящих в двойные системы. Двойной звездой называется такая система из двух звезд, в которой обе они, взаимно притягиваясь, движутся вокруг центра тяжести системы. Подобные системы весьма распространены в звездном мире - в них входит более 20% всех звезд. Двойной звездой оказалась и самая яркая из звезд неба - Сириус. Многолетние наблюдения обнаружили, что ее смещение на небесной сфере не прямолинейно, каким оно должно было бы быть, если бы вызывалось только движением по отношению к Солнцу. Причина, вызывающая искривление пути - присутствие вблизи другой звезды. Она видна лишь в телескоп. Обе звезды движутся по эллиптическим орбитам вокруг центра тяжести системы с периодом около 50 лет. Звезды удалены друг от друга на расстояние в двадцать раз большее, чем Земля от Солнца, т. е. а=20 х 1,5 х 10¹³ см = 3 х 10¹⁴ см. Применяя к системе Сириуса формулу (10), в которую нужно подставить это значение а и величину периода Р в секундах, равную 50 х 365 х 86400 = 1,6 х 10⁹ сек, находим суммарную массу системы. Она равна 6,4 х 10³³ г, т.е. более чем в три раза превосходит массу Солнца. Менее яркая из звезд - спутник - в системе Сириуса является звездой класса А со светимостью в сто раз меньшей, чем у Солнца. Следовательно, эта звезда, называемая Сириус В, представляет собой белый карлик.

Такие двойные системы, у которых, благодаря большому расстоянию между компонентами (составляющими), обе звезды наблюдаются непосредственно, называют визуально-двойными звездами. Из наблюдений визуально-двойных звезд находят расстояние между компонентами а и период обращения Р, что дает возможность по формуле (10) определить и сумму масс компонент. Если наблюдаются движения каждой из компонент в отдельности, а не только относительное движение одной из них, то определяется масса каждой из звезд. Так, например, из рис. 15 можно видеть, что в системе Сириуса спутник - Сириус В - движется вокруг центра тяжести по орбите, размер которой вдвое превосходит размер орбиты главной звезды. Размеры орбит определяются расстояниями тел до центра тяжести системы, а расстояния, как известно из физики, обратно пропорциональны массам тел. Следовательно, масса Сириуса В вдвое меньше массы главной звезды системы. Поскольку общая масса системы Сириуса несколько более трех солнечных масс, масса белого карлика - Сириуса В - приблизительно равна массе Солнца.

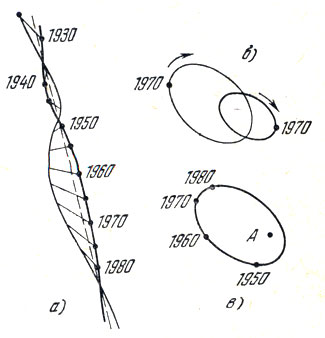
Рис. 15. Видимая орбита Сириуса, а) Жирной кривой показано движение главной звезды, тонкой кривой изображено движение спутника; б) движение компонентов вокруг общего центра тяжести (здесь центр тяжести предполагается неподвижным, а на рис. а) его движение относительно Солнца обозначено прерывистой линией); в) движение спутника вокруг главной звезды.

В том случае, когда в двойной системе компоненты настолько близки, что не разделяются при наблюдении в телескоп, движения их изучают по спектрам. При обращении вокруг центра тяжести системы каждой из звезд, скорость ее по отношению к наблюдателю все время меняется. Это изменение сказывается в периодическом смещении спектральных линий, вызванном эффектом Доплера. Системы, у которых наблюдаются только периодические смещения линий в спектрах, называют спектрально-двойными. Периоды обращения звезд в спектрально-двойных системах сравнительно малы и лишь в редких случаях измеряются годами. Обычно же они составляют несколько суток, а иногда даже доли суток. Наблюдения спектрально-двойных систем также дают сведения о массах звезд, но менее полные, чем получаемые по визуально-двойным звездам.

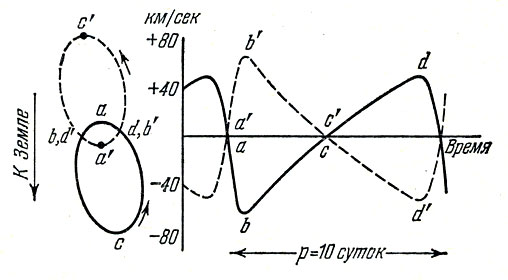
Рис. 16. Движения в спектрально-двойной системе ζ Большой Медведицы. Слева показано движение компонент относительно общего центра тяжести; справа - кривые скоростей компонент.

Расположение звезд в двойной системе может быть таким, что при своем движении звезды по очереди полностью или частично загораживают друг друга от наблюдателя, находящегося на Земле. Луч зрения наблюдателя лежит в орбитальной плоскости (плоскости, в которой движутся звезды) или близок к ней. В этом случае систему называют фотометрической двойной или затменной переменной, так как затмения приводят к видимым изменениям в наблюдаемом излучении системы (рис. 17). Фотометрических двойных систем известно не очень много, потому что ориентация орбитальной плоскости любой двойной системы по отношению к земному наблюдателю является произвольной и только у малой доли систем эта плоскость расположена так, что наблюдаются затмения. Тем не менее, исследование фотометрических двойных систем дало очень много сведений не только о массах звезд, но также о строении звезд и особенностях их свечения.

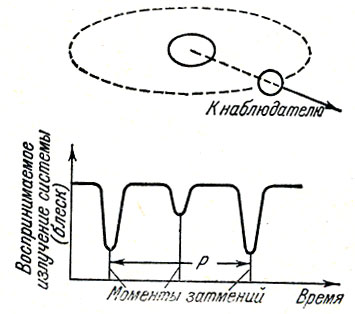
Рис. 17. Схематическое изображение затменной переменной в момент затмения. Кривая представляет периодическое изменение наблюдаемого излучения звезды, вызванное повторяющимися затмениями (вследствие различной яркости обеих звезд изменение блеска в минимуме зависит от того, какая из звезд затмевается).

Итак, наши знания о массах звезд основываются только на результатах изучения двойных систем. Но, как правило, звезды, входящие в эти системы, по всем признакам аналогичны одиночным звездам. Поэтому считают, что имеющиеся данные о массах характеризуют все звезды. У большинства звезд массы не очень сильно отличаются от солнечной. Самая массивная звезда обладает массой приблизительно 100М. У красных карликов массы в 5-10 раз меньше, чем у Солнца.

Обнаружена зависимость между величиной светимости звезды L и ее массой М. Эта зависимость может быть представлена, как пропорциональность светимости приблизительно третьей степени массы: L ~ М³. Она является не строгой, а, как говорят, статистической, т. е. возможны довольно значительные отклонения от этой зависимости в ту или иную сторону. Кроме того, указанной зависимости следуют не все звезды, а лишь звезды главной последовательности. Современные представления о строении звезд позволили получить такую зависимость L от М и теоретически.

Звезды сильно различаются по степени концентрации в них вещества. Концентрацию вещества в звезде можно охарактеризовать значением средней плотности звезды, определяемой как отношение массы к объему, т. е. величиной М_* / (4/3πR³_*). Для средней плотности Солнца, используя приведенные выше значения Mо и Rо, находим значение 1,4 г/см³, что близко к плотности воды. Как мы уже говорили, преобладающим элементом в Солнце является водород. Масса одного атома водорода равна 1,67 х 10^-24 г, и, следовательно, в среднем в Солнце приходится около 10²⁴ атомов на 1 см³. Содержание частиц в одном кубическом сантиметре солнечного вещества оказывается в тысячи раз большим, чем в воздухе у поверхности Земли.

Красные гиганты - представители звездного населения, отличающиеся очень низкой концентрацией вещества. Они содержат в среднем всего 10¹⁵-10¹⁶ атомов в 1 см³, т. е. их плотность в тысячи раз меньше плотности земной атмосферы. Другая крайность - это белые карлики. Так, например, для Сириуса В, имея в виду, что его масса ≈ M, а радиус в сорок раз меньше, чем у Солнца, получаем среднюю плотность, в (40)³=6,4 х 10⁴ раз превосходящую солнечную. Мы видим, что в белых карликах достигается чрезвычайно высокая концентрация атомов: 10²⁹ и больше на 1 см³. Вещество при столь больших плотностях обладает особыми свойствами. В дальнейшем нам неоднократно придется говорить о тех или иных особенностях очень плотных звезд.