§6. ЭНЕРГИЯ КОСМИЧЕСКИХ ТЕЛ

Займемся теперь вопросом о роли различных видов энергии во Вселенной. О важности этого вопроса для интересующей нас проблемы космических взрывов не приходится много говорить, так как все процессы во Вселенной, в том числе и взрывы, связаны с переходом энергии из одной формы в другую. Не зная, в каких формах содержится энергия в данном небесном теле, невозможно понять природу происшедшего на нем взрыва.

Общего определения понятия «энергия» через какие-то другие, более простые понятия в науке нет. Представление же о различных видах энергии и способах вычисления количества энергии того или иного конкретного вида имеется у каждого, изучавшего физику. При всем видимом многообразии форм энергии ее почти всегда можно представить либо как потенциальную, либо как кинетическую энергию, хотя для некоторых видов (например, энергии магнитного поля) это трудно (Подробное и сравнительно доступное обсуждение вопроса о формах энергии читатель может найти в «Фейнмановских лекциях по физике», т. I, гл. 14 (изд-во «Мир», 1965).)

Энергия, зависящая только от взаимного положения тел, называется потенциальной, безразлично, рассматриваем ли мы положение планеты относительно Солнца, положение частицы газа среди других частиц или положение электрона в атоме. Кинетическая же энергия обусловлена движением тел или частиц. Когда движение системы тел или частиц проявляется в достаточно больших, макроскопических, масштабах, то мы говорим о кинетической энергии в обычной форме, изучаемой в механике. Рассматривая движение фотонов, мы также имеем дело с кинетической энергией. И движениям в микромире, например, движениям молекул твердого тела, частиц внутри атома, или атомов в газе соответствует кинетическая энергия. Обычно кинетическую энергию микроскопических движений относят к внутренней энергии тел. Другая часть внутренней энергии создается взаимодействием частиц, составляющих тело, и связана с расположением частиц в теле - это потенциальная энергия.

Огромным числом физических опытов показано, что энергия не может ни исчезать, ни появляться вновь. В этом заключается закон сохранения энергии. Если рассматривать некоторую физическую систему, не учитывая ее взаимодействия с другими системами, то можно утверждать, что в такой системе сумма потенциальной и кинетической энергии остается постоянной. Однако полностью изолировать систему от других тел невозможно и высказанное утверждение верно лишь приближенно. Любая физическая система обменивается энергией с другими телами и в одних случаях этим можно пренебречь, а в других нельзя. Например, изучая движение планет вокруг Солнца, не учитывают действия на них других звезд, поскольку расстояния до звезд очень велики. Но на движении Солнечной системы в целом влияние звезд, составляющих Галактику, сказывается: как мы знаем, в результате их притяжения Солнце движется вокруг центра Галактики. Существуют и другие виды воздействий - какая-то доля излучения звезд доходит до планет, на них падают космические лучи и т. п. Таким образом, сущность закона сохранения энергии не в постоянстве ее количества в данной системе, а в невозможности для энергии исчезнуть или быть созданной.

Как нам уже известно, в доступной наблюдениям области Вселенной основная доля вещества находится в звездах. Поэтому стоит начать изучение распределения энергии во Вселенной именно с оценки энергии, заключенной в звездах. Если не говорить о самых внешних слоях холодных звезд, то можно считать, что звезды состоят из газа, содержащего только ионы и электроны. Так как водород является преобладающим химическим элементом, то число частиц в газе, составляющем звезду, грубо говоря, вдвое больше числа атомов водорода - ведь каждый атом дает две частицы, протон и электрон. Молекулярный вес водорода равен единице и, следовательно, средний молекулярный вес звездного вещества близок к %.

Частицы газа движутся, и их общая кинетическая энергия составляет тепловую энергию, заключенную в звезде. Наряду с этим, каждая из частиц газа притягивает другие по закону всемирного тяготения. Это действие гораздо существеннее, чем электростатическое. Хотя плазма состоит из заряженных частиц, она в целом является нейтральной - в любом достаточно большом ее объеме сумма положительных зарядов равна сумме отрицательных. Следовательно, вещество, находящееся в данном объеме плазмы, не испытывает силы электростатического взаимодействия со стороны другого объема. Этого нельзя сказать о тяготении - действие на любую частицу всех других частиц складывается. Таким образом, потенциальная энергия звезды практически обусловлена только тяготением.

Оценим величину потенциальной энергии звезды. Она определяется работой, которую нужно затратить против сил тяготения, чтобы «разнести» звезду по частицам на такие расстояния, где их действие друг на друга становится ничтожно малым и им можно пренебречь. В этом положении потенциальную энергию можно считать равной нулю. Поскольку для того, чтобы прийти к состоянию тела с нулевой энергией, работа должна быть затрачена, потенциальную энергию тела следует считать отрицательной. Энергия же, за счет которой можно совершить работу, в данном случае тепловая, является положительной.

Вычисление работы против сил тяготения, требуемой для «разнесения» звезды, производится при помощи методов высшей математики. Принцип этого вычисления сравнительно несложен. Предполагают, что от звезды последовательно отрываются тонкие слои вещества и вычисляют работу, которую нужно затратить на удаление каждого из слоев, а затем суммированием находят работу по удалению всех слоев. Точное вычисление возможно также лишь при известной структуре звезды. Поскольку распределение плотности в звезде нам не известно, придется ограничиться только порядковой оценкой величины потенциальной энергии.

Предположим, что от звезды сразу отрывают слой, заключающий в себе половину ее массы, и уносят этот слой на бесконечно большое расстояние. Для упрощения примем также, что масса этого слоя сосредоточена в таком же, как и оставшаяся масса, шаре, т. е. мы считаем, что звезда состоит из двух равных частей, центры которых удалены друг от друга на расстояние , R_*/2, где r - радиус звезды. Сила взаимодействия этих частей определяется формулой (9), в которой нужно положить М₁ = M₂ = М_*/2-масса звезды) и r = R_*/2. Однако и при таком упрощении остается трудность - мы умеем вычислять работу лишь в случае, когда сила постоянна, а при удалении масс друг от друга величина силы уменьшается.

Поскольку сила убывает с расстоянием быстро, мы подсчитаем только ту работу, которая потребуется, чтобы увеличить расстояние между центрами масс вдвое - от R_*/2 до R_*. Силу же на этом пути будем считать постоянной и тем самым в какой-то мере компенсируем неучтенную нами работу на расстояниях, больших, чем R#. Тогда величина потенциальной энергии U получится равной

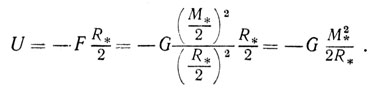
(12)

Вычислим значение U по формуле (12) для Солнца. Ранее мы нашли, что M =2 х 10³³ г, а R = 7 х 10¹⁰ см. При этих значениях получаем, что потенциальная энергия Солнца порядка 10⁴⁸ эрг. Если сделать точное вычисление, то получим величину в шесть раз большую - ведь «дробление» звезды не заканчивается «разнесением» ее на две части.

Следует помнить, что величину U нельзя считать запасом энергии звезды, а, наоборот, это энергия, которая должна была выделиться, если звезда образовалась путем сжатия рассеянного вещества. При уменьшении радиуса звезды, например, вдвое, потенциальная энергия ее U увеличится по абсолютной величине в два раза, оставаясь отрицательной, т. е. будет равной 2U. Следовательно, энергия, равная U, перешла в другие формы. Теоретически запас потенциальной энергии в звезде можно было бы считать неограниченным, если бы радиус звезды мог стать сколь угодно малым. На самом же деле звезда способна сжаться только до некоторого конечного объема, и энергия, выделяющаяся при сжатии, всегда остается конечной.

Можно доказать, опять-таки используя методы высшей математики, важное утверждение, называемое теоремой о вириале. Согласно этой теореме во всякой устойчивой системе частиц, не испытывающих действия внешних по отношению к ней сил и взаимодействующих по закону тяготения, выражаемому формулой (9), имеет место следующая зависимость между потенциальной энергией U и тепловой энергией W системы:

2W = -U, (13)

т. е. удвоенная величина тепловой энергии равна величине потенциальной, взятой с обратным знаком. Звезду с большой точностью можно считать системой частиц, не подверженных внешним воздействиям, потому что другие звезды почти не влияют на составляющие ее частицы. Поэтому формула (13) применима к звезде, и при ее помощи легко оценивается тепловая энергия звезды. Для Солнца она, так же как и потенциальная энергия, порядка 10⁴⁸ эрг, точнее, около 3 х 10⁴⁸ эрг.

Тепловая энергия звезды распределяется на все составляющие звезду частицы, но не в одинаковой мере. В недрах звезды температура выше, чем в ее поверхностных слоях и, соответственно, энергия движения частиц там больше. Тем не менее, интересно вычислить среднюю для всей звезды энергию, приходящуюся на одну частицу. Эта величина позволит найти среднее значение температуры в звезде.

Подсчитаем число частиц в Солнце. Принимая, что оно целиком состоит из водорода, находим число N атомов в Солнце, равное отношению его массы к массе m_H атома водорода (Масса тн получается делением массы грамм-атома на число Авогадро) (m_H=1,67 х 10^-24г). Так как М=2 х 10³³ г, то получаем N≈10⁵⁷. Учитывая, что в Солнце атомы ионизованы, имеем для общего числа частиц в нем значение, примерно равное 2 х 10⁵⁷.

Отношение общей тепловой энергии Солнца к числу содержащихся в нем частиц порядка 10~9 эрг. Средняя энергия частицы газа связана с его температурой формулой (1), из которой при

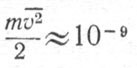
получаем, что температура в недрах Солнца составляет в среднем около 5 х 10⁶°К. В его центральных областях температура выше полученного среднего значения и составляет, как найдено из более подробных расчетов, около 15 миллионов градусов.

Не представляет трудности и оценка величины газового давления внутри Солнца. Для нее можно применить формулу (2). Среднее значение n - числа частиц в 1 см³ солнечного вещества - определяется, как отношение общего числа частиц, только что найденного нами, к объему Солнца, равному 4/3πR³. Выполнив соответствующие вычисления, получим для п значение около 2 х 10²4 частиц/см³, а для давления Р величину Р≈З х 10¹⁵ дин/см², т.е. миллиард атмосфер.

Столь огромная (по земным масштабам) величина давления в недрах звезды может вызвать удивление и даже недоверие. Но легко понять, что звезда при малом давлении в ней просто не могла бы существовать и «спалась» бы к центру под действием собственного тяготения. Действительно, как обстоит дело, например, на Земле? Мы знаем, что вес тела обусловлен притяжением этого тела в направлении к центру Земли. Давление атмосферы - это ее вес, приходящийся на единицу земной поверхности; оно составляет около 1 кГ на 1 см² (Ранее, в § 4, при оценке п не учитывалось, что атомы ионизованы, и поэтому получалась вдвое меньшая величина), что и называют давлением в одну атмосферу. При углублении внутрь Земли к весу атмосферы добавляется вес расположенного над данным уровнем слоя Земли. Давление быстро возрастает с удалением от поверхности в глубь Земли и в ее центральных областях достигает нескольких миллионов атмосфер.

Аналогичное положение имеет место и в звезде. На любом уровне в ней давление определяется весом слоя газа, находящегося над этим уровнем. Так как масса звезды очень велика, то и вес, приходящийся на единицу площади слоя, расположенного, например, посередине между ее центром и поверхностью, гораздо больше соответствующей величины для Земли. Газ, составляющий звезду, может противостоять этому весу лишь благодаря очень большому давлению в нем, которое обусловлено как значительной плотностью, так и высокой температурой вещества.

Вещество, составляющее внутренние области Солнца и других звезд главной последовательности, хотя и обладает очень высокой температурой, по своим свойствам не отличается от обычных газов. Поэтому-то для определения давления в недрах звезд мы пользовались соотношением (2), называемым уравнением состояния. В белых карликах плотность вещества настолько велика, что его свойства необычны и, в частности, уравнение состояния в виде (2) к нему неприменимо.

В недрах белых карликов находится так называемый вырожденный электронный газ .'Поскольку нам в дальнейшем придется иметь дело с объектами очень большой плотности, целесообразно хотя бы кратко сказать здесь о вырожденном газе. Подробно о причинах перехода вещества в вырожденное состояние и свойствах вырожденного газа рассказано в книге С. А. Каплана «Физика звезд» («Наука», 1970).

Концентрация атомов в веществе белых карликов порядка 10³⁰ на 1 см³ и выше. Это значит, что на один атом приходится объем около 10^-30 см³, т. е. кубик со стороной 10^-10 см. Размер кубика в сто раз меньше радиуса ближайшей к ядру орбиты электрона (см. рис. 6). Поэтому в белом карлике не хватает места для того, чтобы атомы могли находиться в целом состоянии и электроны движутся отдельно от ядер.

Движение электронов определяется законами микромира. Один из таких законов, называемый принципом Паули, препятствует более чем двум электронам в атоме двигаться по одной орбите. Вне атома по любому данному пути также не может двигаться с одной и той же скоростью более двух электронов. Если плотность достаточно высока, то места для движения электронов мало и количество возможных путей движения оказывается значительно меньшим, чем число электронов. Такое состояние вещества называется вырожденным. В вырожденном газе на одном и том же пути находится много электронов. Они, в силу принципа Паули, должны обладать различными кинетическими энергиями от нуля до какого-то значения w₀. Чем плотнее вещество, тем больше электронов движется по одному пути и, следовательно, тем выше значение w₀.

Давление, оказываемое электронами, определяется скоростью их движения, т. е., по существу, кинетической энергией. С возрастанием плотности вырожденного газа средняя энергия электронов в нем становится больше, а значит, увеличивается и количество движения, передаваемое ими преграде (или, как мы говорили в § 1, «стенке»). Поэтому давление вырожденного газа зависит главным образом от его плотности ρ (пропорционально ρ ^5/3) и почти не зависит от температуры. Давлением вырожденного электронного газа и уравновешивается сила тяготения в белом карлике.

Вернемся теперь к обычным звездам.

Звезды разных классов различаются по величине температуры и давления в их недрах. Полученные для Солнца значения характерны для большинства звезд. У самых холодных звезд температура в центральной области несколько ниже, но и она составляет несколько миллионов градусов. Газ, обладающий столь высокой температурой, должен излучать огромное количество энергии. Следовательно, внутри звезды должно содержаться, помимо обычного газа, состоящего из частиц вещества, множество фотонов, составляющих «фотонный газ». Подсчитаем общую энергию фотонного газа, т. е. энергию заключенного в звезде излучения.

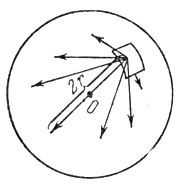
Рис. 23. Распространение излучения внутри шарового объема.

По своим излучательным свойствам недра звезды очень сходны с абсолютно черным телом. Относительно любого объема внутри звезды можно считать, что он поглощает всю падающую на него энергию и поэтому с поверхности, ограничивающей этот объем, должно излучаться столько же энергии,сколько им поглощается. Любая поверхность внутри звезды излучает как поверхность абсолютно черного тела.

Представим себе шаровую поверхность очень малого радиуса г, охватывающую некоторый объем внутри звезды (рис. 23). В этой области, а значит, и на предполагаемой шаровой поверхности температура Т практически одинакова. С поверхности шара внутрь его излучается за 1 сек количество энергии, равное 4πr²σТ⁴. Фотоны находятся внутри шара лишь то время, которое им требуется, чтобы пролететь сквозь него со скоростью с (Если часть фотонов поглощается, то вместо них в этом объеме образуется такое же число фотоно». Поэтому в данном рассуждении поглощение излучения можно не принимать во внимание.) Фотон, движущийся вдоль радиуса, затрачивает на путь сквозь шар время -2r/с . Но фотоны испускаются поверхностью во всех направлениях и летят не только вдоль диаметра шара, но и по хордам. Более детальный расчет позволяет найти, что путь фотона в шаре в среднем составляет 4/3 r. Следовательно, в каждый данный момент в объеме шара содержится энергия излучения, равная

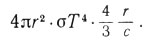
Разделив полученную величину на объем шара

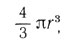
найдем плотность излучения, т. е. количество энергии излучения, приходящейся на 1 см³. Как мы видим, она равна - 4σ/сТ⁴. Точно вычислить общее количество энергии излучения в звезде изл можно лишь при известных значениях Т для каждой области звезды. Однако правильный порядок величины ?изл получим, умножив плотность излучения, соответствующую средней температуре звезды, на объем звезды:

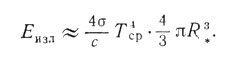
(14)

В (14) величина R_* означает радиус звезды. Используя известные значения Т_ср и R_* для Солнца, мы находим, что Еизл≈10⁴³ эрг. Таким образом, энергия излучения, заключенного в Солнце, гораздо меньше, чем его тепловая энергия. Это же справедливо и для других звезд.

Звезда непрерывно излучает энергию со своей поверхности в пространство, причем это есть, по существу, излучение нагретого газа и обеспечивается оно тепловой энергией звезды. Тепловая энергия, содержащаяся в звезде, должна все время восполняться, иначе она за сравнительно короткий срок вся израсходуется на излучение. Например, для Солнца, излучающего ежесекундно 3,9 х 10³³ эрг, заключенной в нем тепловой энергии не хватило бы даже на тридцать миллионов лет. Мы же знаем, хотя бы по данным геологии, что излучение Солнца было приблизительно таким же, как и в настоящее время, более миллиарда лет.

Очевидно, что затраченная на излучение энергия Солнца не могла сколько-нибудь существенным образом пополниться за счет преобразования потенциальной энергии. Даже если Солнце возникло из очень разреженного облака, потенциальная энергия которого (в указанном выше смысле) была близка к нулю, то освободившаяся при сжатии облака до теперешнего размера Солнца энергия порядка 10⁴⁸ эрг не могла обеспечить столь длительного свечения.

Аналогичная ситуация имеет место и для других звезд, по крайней мере тех из них, которые близки по своей светимости и массе к Солнцу. Значит, в звездах существуют какие-то возможности пополнения тепловой энергии -запасы энергии в скрытом виде. Оценка этих запасов станет для нас возможной после того, как мы ознакомимся с одним из очень важных положений теории относительности, а именно с эквивалентностью массы и энергии.

Теория относительности заставила отказаться от привычного представления о массе тела, как величине постоянной. Оказывается, что масса зависит от скорости движения тела. Изменение величины массы как меры сопротивления тела действию на него силы обусловлено законом сохранения количества движения. Количество движения не может возникнуть из ничего, без участия силы. Если, в частности, сила F, действующая на тело, постоянна, то за время t она изменит количество движения mv (тm- масса тела, v -его скорость) от величины (mv)_о до значения (mv)_t, причем

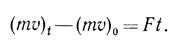
Одно из основных положений теории относительности состоит в том, что невозможно никакое движение со скоростью, большей чем скорость света с. Если скорость тела в начале действия силы была уже близка к с, то сколько бы сила ни действовала, она не может существенно ее увеличить. Количество же движения будет возрастать и при достаточно большом времени действия силы величина (tnv)t может стать сколь угодно большой. Следовательно, при скоростях движения, близких к с, масса тела под действием силы растет, т. е. увеличивается сопротивление, оказываемое телом изменению состояния его движения. Чем быстрее движется тело, тем больше его инерция. Зависимость массы тела от скорости его движения определяется формулой

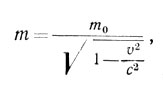
вывод которой потребовал бы слишком много места и поэтому здесь мы его не приводим. С ним можно познакомиться, в частности, по книге «Беседы о теории относительности» Б. Г. Кузнецова (Изд. АН СССР, 1963).

Величина m_о представляет собой значение массы при равной нулю скорости и называется массой поко Зависимость массы от скорости сказывается лишь при значениях v в десятки тысяч километров в секунду. Даже при огромной в земных условиях скорости v=1000 км/сек и, соответственно, величине v²/c² = 1/90000, значение mо отличается от mо менее, чем на 0,002%. Поэтому изменение массы, вызванное движением, заметно только у очень быстрых частиц, движущихся со скоростью, близкой к скорости света, например у частиц, разгоняемых магнитным полем в ускорителе (синхрофазотроне), или у частиц, составляющих космические лучи. Если v/c намного меньше единицы, то соотношение (16) между массой и скоростью приближенно можно записать в виде

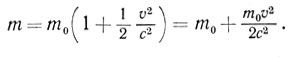
(17)

При v/c ≤ 1/10 это соответствие верно с точностью до 0,005% (Так при v/c достаточно малых v⁴/с⁴ очень мало по сравнению с v²/c², то имеем

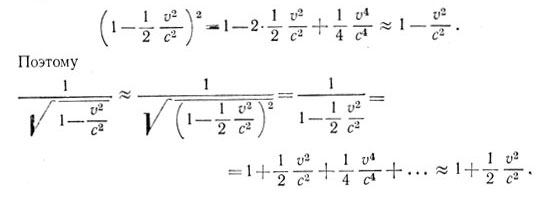
Здесь мы воспользовались известной формулой для суммы бесконечной геометрической прогрессии (со знаменателем в данном случае 1/2 v²/с²))

Таким образом, оказывается, что вследствие движения тела масса его увеличивается на величину кинетической энергии, деленной на с². Если это увеличение массы, равное m-m_о, обозначить Δm, то получим важную формулу

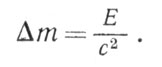
Сделанное нами ограничение, что v намного меньше с, вызвано только стремлением к упрощению вывода и не является существенным. Эта формула верна при любом значении v/c.

Соотношение (18) устанавливает связь между массой и энергией. Хотя оно нами здесь выведено для случая, когда Е - кинетическая энергия, но, поскольку эта энергия есть результат преобразования энергии других видов, можно утверждать, что всякой энергии соответствует некоторая масса. Энергия и масса не одно и то же: говорят, что они эквивалентны, т. е. изменение энергии тела всегда пропорционально изменению его массы.

Вследствие эквивалентности массы и энергии, телу свойственна определенная энергия, если оно и не движется. Массе покоящегося тела, равной m_о, соответствует энергия покоя Е_о = m_ос². При некоторых условиях энергия Е_о может превратиться в другие виды энергии, например, в излучение. Такое превращение называют аннигиляцией («уничтожением»). То, что процессы аннигиляции наблюдаются в действительности, блестяще подтверждает заключение теории относительности о связи массы и энергии. Одно из таких многократно наблюдавшихся явлений - аннигиляция электрона при встрече с другой частицей, называемой позитроном. По своей массе и по величине электрического заряда эти частицы не отличаются друг от друга, но знаки зарядов у них противоположны. Соединяясь, электрон и позитрон перестают существовать и при этом возникает излучение. Энергия получившихся фотонов составляет 1,6 х 10^-6эрг, что в точности равно произведению удвоенной массы электрона 2x9 х 10^-28г на квадрат скорости света.

Массе звезды М_* соответствует энергия М_*с². Для Солнца, например, Мс²=1,8 х 10⁵⁴ эрг. Это значение в сотни тысяч раз превышает тепловую энергию Солнца, что и понятно, поскольку средние скорости движения частиц, составляющих Солнце, малы по сравнению со скоростью света. Величина М_*с² определяет полный запас энергии звезды. Но далеко не вся эта энергия может в условиях звезды перейти в другие виды энергии.

Полная аннигиляция возможна только в том случае, когда частицы и соответствующие античастицы содержали в одинаковом количестве. О Солнце и других звездах Галаю тики нет оснований думать, что они в сколько-нибудь существенной части состоят из антивещества. Поэтому хотя в них и вырабатывается энергия путем рассматриваемых ниже термоядерных реакций, но это приводит лишь к незначительному уменьшению массы звезды.

Определим изменение массы вещества в результате выработки энергии при реакциях так называемого протон-протонного цикла. Эти реакции, по современным воззрениям, являются источником энергии свечения Солнца и подобных ему звезд. Они сводятся к образованию ядер атомов гелия из ядер атомов водорода - протонов.

Ядра всех атомов, кроме водорода, являются сложными. Они состоят из положительно заряженных частиц - протонов и частиц почти такой же массы, лишенных заряда -нейтронов. Напомним, что ядро атома гелия (называемое также α-частицей) состоит из двух протонов и двух нейтронов. Частицы в ядре атома связаны особыми внутриядерными силами, действие которых сказывается только при очень малых расстояниях между частицами. Для того чтобы удалить, например, из α-частицы протон, нужно произвести работу против внутриядерных сил, т. е. затратить энергию. Эта энергия называется энергией связи протона в α-частице. При соединении же двух протонов и двух нейтронов в α-частицу должна освобождаться энергия, равная их энергии связи.

Не останавливаясь пока на условиях, при которых может происходить образование частиц из протонов, рассмотрим последовательные этапы этого цикла. Если при встрече двух протонов (мы обозначаем протон буквой р) им удастся достаточно сблизиться, то возможно образование ядра атома дейтерия (тяжелого водорода D₂), которое состоит из протона и нейтрона. Нейтрон, входящий в состав D², получается из протона. Превращение протона в нейтрон сопровождается испусканием положительно заряженной частицы - позитрона е+ (о ней мы уже говорили выше), и особой частицы, не имеющей заряда - нейтрино (обозначают ее v). Кроме того, при соединении частиц выделяется фотон очень большой энергии - γ-квант. Реакция образования D² схематически записывается следующим образом:

р + p→D² + e⁺ + v + γ. (I)

Позитрон е⁺ в дальнейшем аннигилирует, встретившись с каким-либо свободным электроном, и при этом получаются еще два γ-кванта.

Ядро дейтерия, соединяясь с достаточно близко подошедшим к нему протоном, образует новую частицу - ядро изотопа гелия Не³, содержащее два протона и нейтрон. Эта реакция также протекает с выделением энергии в виде γ-кванта:

D²+р→Не³ + γ. (II)

Получившееся ядро Не³ может вступать в различные реакции, но в звездах наиболее частой является реакция между двумя частицами Не³. Она происходит согласно следующей схеме:

Не³ + Не³→Не⁴ + р + р + γ, (III)

т. е. ведет к образованию а-частицы (Не4), двух протонов и у-кванта.

Таким образом, в итоге протон-протонного цикла реакций вместо четырех протонов получаются а-частица, несколько γ-квантов и нейтрино. Масса покоя а-частицы m_не⁴ меньше массы четырех протонов 4m_р. Величина разности 4m_р-m_не⁴. и определяет количество вещества, эквивалентного выделившейся энергии, а отношение

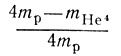
есть доля массы, соответствующей энергии, вырабатываемой в реакциях протон-протонного цикла. Она составляет

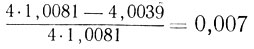
(значения масс здесь взяты в единицах атомного веса). Как мы видим, масса вещества в результате протон-протонного цикла уменьшается всего на семь десятых процента от массы водорода, содержавшегося в веществе. Преобразование всего водорода, содержащегося в Солнце, в гелий может дать

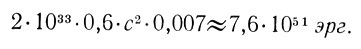
При наблюдаемом в настоящее время расходе энергии на излучение, этого количества должно хватить на 2 х 10¹⁸ сек, т. е. на десятки миллиардов лет.

Термоядерные реакции происходят в плазме лишь при определенных условиях, не реализующихся, например, во внешних слоях звезд или в межзвездной среде. Далеко не при каждой встрече двух протонов образуется ядро атома дейтерия. Протоны, как одинаково заряженные частицы, испытывают действие электростатического отталкивания, тем большее, чем ближе они находятся друг к другу. Протон как бы окружен преградой, препятствующей сближению с ним другой положительно заряженной частицы. Поэтому употребляют особое выражение - говорят, что у протона существует потенциальный барьер. Внутриядерные же силы притяжения очень быстро убывают с расстоянием и только при расстояниях между частицами порядка 10^-13см или меньших они превосходят силы электростатического отталкивания. Следовательно, ядро атома дейтерия образуется лишь в том случае, когда относительная скорость сталкивающихся протонов настолько велика, что соответствующая ей кинетическая энергия достаточна для преодоления потенциального барьера. Один из протонов, пробившись через барьер в область действия внутриядерных сил, превращается там в нейтрон. Аналогичный потенциальный барьер одноименно заряженным частицам приходится преодолевать и при других термоядерных реакциях.

Если температура плазмы недостаточно высока, скажем, 3-5 миллионов градусов, то протонов с необходимым для преодоления потенциального барьера значением скорости почти нет и протон-протонная реакция не идет. При температурах же, близких к 15 миллионам градусов, сравнительно большая доля частиц имеет энергию, позволяющую им подойти к другой частице достаточно близко для образования более сложного ядра. Таким образом, одно из необходимых условий протон-протонного цикла -это высокая температура плазмы, близкая к 15 х 10⁶°К. С другой стороны, для того чтобы встречи протонов происходили часто, требуется высокая концентрация этих частиц. Оба эти условия выполняются в центральных областях Солнца и сходных с ним звезд. Водород является преобладающим элементом в Солнце и в недрах его ионизован. Число протонов в центральных областях Солнца составляет примерно 10²⁶ см^-3, а температура там 15 миллионов градусов. Идущие в Солнце реакции протон-протонного цикла обеспечивают наблюдаемый выход энергии излучения 3,9 х 10³³ эрг/сек.

Энергия при протон-протонном цикле выделяется преимущественно в форме γ-квантов и при взаимодействии с веществом звезды превращается в тепловую энергию. Некоторая часть энергии уносится нейтрино. Эта частица обладает замечательным свойством - она настолько слабо взаимодействует с любыми другими частицами, что практически беспрепятственно проходит сквозь толщу Солнца. Поток нейтрино из Солнца и других звезд пронизывает все пространство и находящиеся в нем тела, включая Землю, не производя при этом никаких непосредственно заметных эффектов.

Температура в центральных областях звезды в сотни раз превышает ее поверхностную температуру. Из физики известно, что тепло переходит от тела с высокой температурой к более холодному. Поэтому тепловая энергия из недр звезды распространяется в наружные слои. Достигнув поверхности звезды, энергия уходит в пространство в форме излучения. Перенос тепла может осуществляться разными способами - лучеиспусканием, теплопроводностью и конвекцией. У большинства звезд лучеиспускание является основным способом передачи энергии от внутренних слоев к наружным. В этом случае энергия переносится фотонами. Если бы вещество звезды было столь же прозрачным для фотонов, как и для нейтрино, то фотон, возникший в недрах звезды, двигаясь со скоростью 3 х 10¹⁰ см/сек, потратил бы на путь до поверхности несколько секунд. Но на самом деле очень плотный газ, из которого состоит звезда, непрозрачен, т. е. в сильной степени поглощает фотоны. Вследствие этого излученный фотон проходит лишь какое-то малое расстояние l, называемое длиной пробега, после чего поглощается веществом. Длину пробега фотона нетрудно оценить, например, для Солнца.

Выделим мысленно внутри Солнца на уровне R≈0,5R шаровой слой толщины l. Температура на этом уровне близка к 3 x 10⁶ °К, и энергии за счет термоядерных реакций в нем не выделяется. Будем считать слой прозрачным для излучения и, так как радиусы внешней и внутренней поверхностей очень близки, примем их одинаковыми. Так как температура в Солнце убывает от центра наружу, то ее значение на внутренней поверхности слоя - обозначим его Т₂ - больше, чем значение температуры T₁ на внешней поверхности. Мы знаем, что любая поверхность внутри звезды излучает как абсолютно черное тело. Поэтому, согласно формуле (6), за секунду с внутренней поверхности слоя излучается наружу энергия, равная 4πR²σT⁴₂, а с внешней излучается внутрь энергия 4πR²σT⁴₁. Излучение, выходящее с поверхности Солнца за секунду, обеспечивается за счет различия этих энергий и, следовательно, 4πR²σ(Т⁴₂ - Т⁴₁) = 4πR²σТ⁴. Примем, что температура с уровня R до поверхности меняется равномерно (На самом деле температура меняется с расстоянием от центра звезды более сложным образом, но это не сказывается на порядке величины l). Тогда

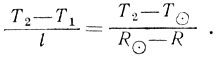
Так как

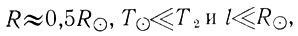
то, разложив разность Т⁴₂ - Т⁴₁ на множители и учитывая, что (Т₂+ Т₁)(T²₂ - Т²₁)≈4Т³₂, для длины пробега фотона получаем величину

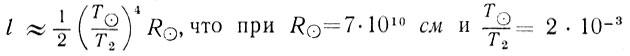
дает значение l≈0,6 см.

Так как длина пробега фотона очень мала по сравнению с радиусом звезды, то фотоны на своем пути из центра звезды наружу должны поглощаться и вновь излучаться огромное число раз. Поэтому выход наружу энергии, выработанной в недрах звезды, занимает очень большое время - миллионы и даже десятки миллионов лет.

Процесс теплопроводности, заключающийся в переносе тепловой энергии частицами - например, электронами,- в звездах малоэффективен и требует еще большего времени, чем перенос лучеиспусканием. Дело в том, что частицы движутся медленнее фотонов и, кроме того, длина пробега для частицы во много раз меньше, чем для фотона.

Хотя взрывы внутри звезд будут обсуждаться позже, уже сейчас на основе проведенных подсчетов можно сделать вывод о том, что ни лучеиспускание, ни тем более теплопроводность не способны обеспечить достаточно быстрый выход энергии взрыва в наружные области звезды, где она станет наблюдаемой. Излучение, возникшее при взрыве внутри звезды, при условии, что структура звезды сохраняется, должно выходить наружу постепенно - в течение миллионов лет. Весь эффект будет настолько «размазан» во времени, что его заметить не удастся.

Гораздо быстрее может переноситься энергия из недр звезды к ее поверхности путем конвекции, т. е. при перемещении нагретых масс газа в области с более низкой температурой. Однако конвекция развивается только при определенных условиях, которые реализуются далеко не во всех звездах и чаще всего лишь в их внешних слоях.

Если какой-то массе газа внутри звезды сообщена дополнительная тепловая энергия и температура газа становится выше, чем в окружающей среде, то увеличившееся давление заставляет газ расшириться. При этом плотность его уменьшится и он, по закону Архимеда, всплывает - движется к поверхности. Давление от центра звезды уменьшается, и нагретый газ, всплывая, продолжает расширяться. Как известно из школьного курса физики, при расширении газ охлаждается. Поэтому дальнейшая судьба всплывающего газа зависит от того, насколько быстро меняется температура в звезде вдоль ее радиуса. Если она уменьшается недостаточно быстро, всплывающий объем через некоторое время охладится до температуры окружающей среды и его движение прекратится. Конвекции в этом случае не происходит. При быстром падении температуры в звезде вдоль радиуса всплывающий газ, несмотря на охлаждение, остается горячее окружающей его среды и движение продолжается до тех пор, пока он не попадает в самые внешние слои звезды. Там нагретый газ излучает содержащуюся в нем энергию в пространство, остывает, становится более плотным и тонет в окружающем газе.

Скорости движения масс газа при конвекции порядка 100 м/сек, а время, за которое нагретый газ переходит из недр во внешние слои звезды, равно 10-20 суткам. Это действительно очень малая величина по сравнению со временем, которое фотоны в звезде тратят на прохождение того же пути.

Мы изучили содержание энергии различных видов в звезде и способы переноса энергии в звездах. Все описанные виды энергии относятся к внутренней энергии звезды. Но звезда обладает и механической энергией, обусловленной, во-первых, движением ее как целого и, во-вторых, взаимодействием звезды с другими телами, входящими в звездную систему.

По наблюдаемым спектрам звезд было обнаружено, что многие из них сравнительно быстро вращаются вокруг своей оси. Скорость движения на экваторе звезды, созданная вращением, составляет десятки, а иногда даже сотни километров в секунду. Медленное вращение, приводящее к экваториальным скоростям в несколько километров в секунду, по спектрам звезд заметить трудно. Однако хорошо известно, что Солнце вращается и линейная скорость вращения на его экваторе равна 2 км/сек. Можно полагать, что звезды, у которых по спектрам не удалось обнаружить вращения, все же обладают вращательной скоростью такого же порядка или даже несколько большей.

Значение скорости в различных точках внутри вращающейся звезды не одинаково и зависит от расстояния данной точки от оси вращения. Поэтому для точного вычисления кинетической энергии необходимо знать распределение вещества внутри звезды. Если считать, что вещество звезды не очень сильно сконцентрировано в ее центральных областях, то порядковую оценку кинетической энергии вращения можно получить, приняв всю массу звезды сосредоточенной на одном и том же расстоянии от оси вращения, скажем, на расстоянии R_*/2, где R_*-радиус звезды. При угловой скорости вращения, равной ω, линейная скорость массы в этой модели составит 2πR_*/2ω и для кинетической энергии вращения E_вр получится формула

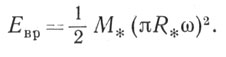
Так как находимая из наблюдений Солнца линейная скорость на его экваторе 2πRω = 2 x 10⁵ см/сек, то для его энергии вращения получаем величину E_вр≈10⁴³ эрг. Она мала по сравнению с тепловой энергией. У звезды, вращающейся с большой скоростью, например, 300 км/сек, на экваторе, энергия вращения может достичь 10⁴⁷ эрг. Указанное значение скорости близко к предельно возможному, потому что при существенно большей скорости звезда должна быть разорвана на части центробежными силами. Следовательно, даже у наиболее быстро вращающихся звезд энергия вращения меньше тепловой энергии (Так как на поверхности многих звезд существуют магнитные поля, следовало бы оценить и магнитную энергию звезды. Сейчас это сделать трудно, поскольку нам неизвестны поля внутри звезд. Вероятно, магнитная энергия значительно меньше тепловой.).

Механическая энергия звезд, входящих в двойную систему, может быть весьма значительной. Пусть, например, две звезды с массами, равными солнечной (М₁ = М₂=М), вращаются вокруг общего центра тяжести, причем расстояние а между ними такое же, как от Солнца до Земли. Поскольку скорость V у обеих звезд одна и та же, то их кинетическая энергия равна 1/2 (M₁ + М₂)V²=МV². Скорость V связана с периодом обращения соотношением

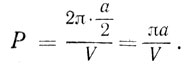
Используя это соотношение и формулу (10), получаем, что

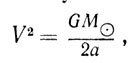
а кинетическая энергия их

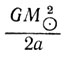
При а = 1,5 х 10¹³ см, кинетическая энергия звезд составляет 10⁴⁶ эрг. В случае же, когда расстояние между компонентами системы в сто раз меньше (такие системы встречаются сравнительно часто), их энергия равна 10⁴⁸ эрг, т. е, такого же порядка, как и тепловая энергия звезд. Таким образом, чем более тесной является двойная система, тем больше энергия входящих в нее звезд. Этот вывод следует, как легко видеть, и из теоремы о вириале (соотношение (13)).

В звездных системах, занимающих большой объем и содержащих много звезд, таких, как шаровые скопления, Галактика, помимо кинетической энергии звезд и туманностей и потенциальной энергии их тяготения, содержится «рассеянная» энергия. В нее включается энергия различных излучений, в частности, излучения звезд, космических лучей и магнитная энергия, распределенные по всему пространству, занимаемому звездной системой.

Каждая из звезд Галактики обладает собственным, так называемым пекулярным движением относительно других звезд. Эта скорость в среднем равна 10-20 км/сек. Следовательно, на каждую звезду приходится кинетическая энергия порядка 10⁴⁵-10⁴⁶ эрг. Скорости звезд, вызванные вращением всей Галактики вокруг ее центра, больше пекулярных, и составляют несколько сотен километров в секунду.Это дает около 10⁴⁸ эрг на каждую звезду Галактики, а на всю систему 10⁵⁹-10⁶⁰ эрг. Согласно теореме о вириале такого же порядка должна быть и потенциальная энергия Галактики.

Величина «рассеянной» энергии в Галактике в тысячи раз меньше полученной величины механической энергии и, по-видимому, не превышает 10⁵⁶ эрг. Поскольку плотность этой энергии - содержание энергии в единице объема - очень мала, большое количество ее не может достаточно быстро перейти в другие виды и, вероятно, роль таких форм энергии в возникновении космических взрывов не столь существенна, как энергии, сосредоточенной в плотных небесных телах.