2. Динамо-теории солнечных циклов

Как уже отмечалось в предыдущем разделе, за последнее десятилетие наиболее детально были разработаны динамо-теории солнечных циклов, основная цель которых состояла в том, чтобы показать, как в условиях высокой электропроводности, присущих солнечной плазме, может генерироваться крупномасштабное магнитное поле Солнца. Однако это лишь самая общая задача таких моделей. Если же говорить точнее, то они должны дать удовлетворительное объяснение основных свойств солнечной активности, которые, судя по тому, что уже узнал из этой книги читатель, вкратце сводятся к следующему:

1) для числа групп солнечных пятен выполняются законы Швабе - Вольфа и Шперера;

2) угловая скорость вращения (по крайней мере атмосферы) Солнца максимальна на экваторе и постепенно убывает к полюсам, т. е. для нашего дневного светила характерно дифференциальное вращение;

3) магнитные поля ведущего и хвостового пятен групп имеют противоположную полярность в северном и южном полушариях Солнца; эта полярность изменяется на противоположную при переходе от одного 11-летнего цикла к другому;

4) полярное магнитное поле Солнца меняет свою полярность на противоположную вблизи эпохи максимума 11-летнего цикла;

5) ведущие пятна групп обычно отличаются большими размерами и существуют дольше, чем хвостовые; как правило, они расположены ближе к экватору Солнца, причем угол наклона оси групп к экватору возрастает с удалением от него;

6) наиболее крупные группы солнечных пятен нередко появляются вновь в тех долготных интервалах, в которых они уже были замечены ранее, т. е. существуют активные долготы пятен;

7) в хромосфере наблюдаются спиральные «вихри», направление которых чаще всего не совпадает с направлением силовых линий магнитного поля в этих областях;

8) появление биполярных магнитных областей лежит в основе развития групп пятен и активных областей; однако иногда они не связаны с другими видами активных образований, в особености, когда они слабые и расположены у полюсов Солнца;

9) при возрастании напряженности магнитного поля этих областей сначала появляются факельные площадки, а затем солнечные пятна, которые исчезают в обратном порядке по мере увеличения площади магнитных областей и ослабления напряженности их поля;

10) водородные волокна и протуберанцы обычно существуют лишь над старыми магнитными областями, разделяя их на две части с полями противоположной полярности.

Модель Бэбкока явилась первой из таких теорий, хотя и не содержала решения уравнений магнитной гидродинамики и даже не пыталась их решать. Она была лишь достаточно широким обобщением наблюдений Солнца с применением известных к началу 60-х годов теоретических разработок. В частности, случилось так, что она вобрала в себя и идеи «зачинателя» динамо-теорий солнечных циклов американского астрофизика Е. Паркера. В этом смысле модель Бэбкока была не только предтечей, но и первой из моделей подобного рода, хотя ее создатель своей статье, содержавшей ее изложение, дал очень скромное название: «Топология магнитного поля Солнца и 22-летний цикл».

Как мы уже знаем (см. раздел 4 главы 1), магнитное поле Солнца состоит из двух составляющих: более сильного тороидального (или азимутального) поля, вытянутого вдоль параллелей и в основном расположенного ближе к солнечному экватору, и полоидального поля, вытянутого вдоль меридианов и расположенного в полярных областях. Считают, что полоидальное магнитное поле дипольного характера является отражением его общего поля. Мы уже говорили о высокой электропроводности солнечной плазмы. Эта особенность накладывает свой отпечаток на ее взаимодействие с магнитным полем. Даже вблизи солнечной фотосферы электропроводность в принципе можно считать бесконечно большой. А если это так, то магнитный поток через любой проводящий контур большого размера (что характерно для Солнца) не изменяется практически в течение бесконечно большого интервала времени. Если этот поток изображен в виде трубки магнитных силовых линий, то можно сказать, что силовые линии «вморожены» в проводящую среду. Таким образом, движение солнечной плазмы увлекает за собой и магнитные силовые линии, и если линия проходит через какие-то массы плазмы, то она будет проходить через них и в дальнейшем. Вмороженность приводит к тому, что магнитное поле усиливается при сжатии плазмы и ослабляется при ее расширении.

Согласно гипотезе Бэбкока, общее магнитное поле Солнца представляет собой диполь с силовыми линиями, расположенными в меридиональных плоскостях между широтами ±55° под видимой поверхностью на глубине не более 30 - 80 тысяч километров. На низких шпротах они находятся ближе к солнечной фотосфере, вблизи северного полюса выходят наружу до расстояния в несколько солнечных радиусов и затем входят внутрь Солнца вблизи его южного полюса. Вследствие дифференциального вращения Солнца на сравнительно низких широтах силовые линии полоидального поля вытягиваются в довольно тонкие спирали вдоль параллелей по обе стороны от экватора, и таким образом в «королевских зонах» это поле превращается в тороидальное. В результате поле усиливается, причем степень этого усилия зависит от широты. Когда напряженность магнитного поля достигает в какой-то части спирали критической величины, равной, согласно Бэбкоку, 250 Гс, там создается неустойчивость. Вследствие того, что в магнитной области плотность вещества меньше, чем в окружающей среде, на эту область начинает действовать сила, которая приводит к ее всплыванию. Кроме того, скручивание магнитных силовых трубок (которое может вызываться искажениями, создаваемыми переносом энергии вещества на поверхность постоянной угловой скорости) тоже усиливает поле и делает их неустойчивыми. В итоге образуются петли, которые при напряженности поля около 1000 Гс всплывают над видимой поверхностью Солнца. Так возникают биполярные магнитные области (рис. 17).

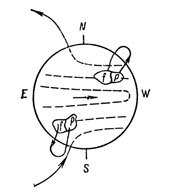
Рис. 17. Возникновение биполярных магнитных областей по гипотезе Х. В. Бэбкока. Штриховые линии показывают направление силовых линий подфотосферного тороидального магнитного поля, образованного из полоидального поля (p - ведущая, а - последующая часть области).

Критическое значение напряженности поля достигается примерно через три года после закручивания магнитных силовых линий вдоль параллелей на широтах ±30°, т. е. именно там, где обычно появляются первые солнечные пятна нового 11-летнего цикла. По мере развития цикла эта критическая величина может быть достигнута на все более близких к экватору Солнца широтах, в соответствии с законом Шперера. Бэбкок, а затем чехословацкий астрофизик М. Крпецкий вывели уравнение, связывающее широту, на которой получается критическое значение напряженности поля, с фазой 11-летнего цикла. Оно дает результаты, очень неплохо согласующиеся с наблюдениями.

После появления биполярной магнитной области вследствие дифференциального вращения Солнца она движется вперед по отношению к магнитной силовой трубке, расположенной под фотосферой. Благодаря этому напряженность поля в ведущей части области выше, чем в хвостовой части. Вот почему обычно ведущее пятно группы преобладает над хвостовым. Постепенно магнитная область расширяется, но при этом ее ведущая часть всегда остается более устойчивой и сильной. По мере расширения области ее магнитные силовые линии движутся наружу в общее поле Солнца. При этом они то соединяются, то разъединяются, и следовательно, такой процесс неизбежно связан с нейтрализацией какой-то части общего поля. Ведущие части биполярных магнитных областей расширяются к экватору, тогда как хвостовые смещаются к полюсам. В результате вблизи экватора происходит нейтрализация ведущих частей биполярных магнитных областей, а вблизи полюсов объединение их хвостовых частей постепенно создает новое полоидальное поле Солнца противоположной полярности (рис. 18). Согласно расчетам Бэбкока такое смещение к полюсам хвостовых частей разрушающихся биполярных магнитных областей может произойти за первые несколько лет 11-летнего солнечного цикла. Поэтому изменения полярности общего магнитного поля Солнца следует ожидать не в эпоху минимума 11-летнего цикла, а скорее в эпоху его максимума. Более того, такое объяснение вполне допускает, что обращение знака поля в северном и южном полушариях Солнца может происходить не одновременно.

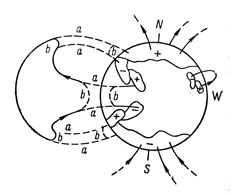
Рис. 18. Обращение знака полоидального магнитного поля по гипотезе Х. В. Бэбкока. Силовые линии старых магнитных полей расширяются. В результате их взаимодействия с полоидальным полем участки линий b и поле частично нейтрализуется. В конечном итоге происходит обращение знака поля.

Таким образом, гипотеза Бэбкока объясняет закон Шперера, закон изменения полярности магнитного поля солнечных пятен при переходе от одного 11-летнего цикла к другому, обращение знака общего магнитного поля Солнца и расширение биполярных областей при их разрушении. К сожалению, она, в сущности, не рассматривает вопрос об источнике энергии, поддерживающей дифференциальное вращение Солнца. А ведь дифференциальное вращение в этой гипотезе имеет ключевое значение. Подход к решению этого вопроса был найден сравнительно недавно. Оказалось, что таким источником вполне может быть конвекция в подфотосферном слое. И в настоящее время вряд ли можно найти гипотезу о происхождении солнечной цикличности, которая бы столь полно использовала все имеющиеся данные наблюдений солнечной активности, как гипотеза Бэбкока.

Следующий важный шаг в создании динамо-теорий солнечных циклов сделал американский астрофизик Р. Лейтон. В отличие от Бэбкока, удовлетворившегося построением чисто качественной модели, он создал полуколичественную модель цикла солнечной активности. Он занимался решением магнитогидродинамических уравнений и вместе с тем не мог не опираться на фактические данные наблюдений Солнца. В основе модели Лейтона тоже лежит усиление магнитного поля дифференциальным вращением. Модель эта во многом сходна с моделью Бэбкока. Но, в отличие от последней, она учитывает связь между активными процессами на различных широтах Солнца. Кроме того, в этой модели магнитное поле никогда не является чисто полоидальным, а зона пятнообразования не только смещается к экватору, но и расширяется с ходом 11-летнего цикла. Наконец, в модели Лейтона не требуется введение магнитных силовых трубок. Поэтому она заменяет дискретную картину закона Шперера, присущую гипотезе Бэбкока, непрерывной.

Обратимся теперь непосредственно к динамо-теориям солнечных циклов, или, выражаясь более точно, теориям гидромагнитного солнечного динамо. Долгое время создание таких теорий считалось вообще неразрешимой задачей. К такому выводу привело рассмотрение простейших осесимметричных движений на Солнце, которые, как было строго доказано, не в состоянии поддерживать устойчивое магнитное поле. Но в 1955г. Паркер сделал решительный шаг, который превратил невозможное в реально осуществимое, предложив (правда, в самой общей, эвристической форме) производить усреднение уравнений магнитной гидродинамики по составляющим среднего магнитного поля (т. е. поля, усредненного по долготе). Кроме того, он объединил этот прием с эффектом несимметричного поднимания петель, т. е. с несимметричными мелкомасштабными движениями в конвективной зоне Солнца. Как это нередко случается, сначала на идеи Паркера не обратили внимания, а затем о них вообще забыли почти на десять лет. И вспомнили об этой работе, только когда советский физик С. Н. Брагинский и астрофизики из ГДР М. Штейнбек, Ф. Краузе и К.-Х. Редлер уже не в форме прикидки, а вполне строго предложили два подхода к решению задачи гидромагнптного динамо. Первый из них, принадлежащий Брагинскому, опирается на то, что среднее магнитное поле может поддерживаться даже при слабом отклонении движений от осевой симметрии. Такой подход вполне оправдан при высокой электропроводности жидкости, характерной Для подфотосферного и фотосферного слоев Солнца. Тогда если магнитное поле преимущественно тороидальное, то неосесимметричные движения действительно могут создавать эффективную электродвижущую силу, которая создает тороидальный ток, генерирующий полоидаль-ное поле. Вспомним, что дифференциальное вращение Солнца может превратить его полоидальное магнитное поле в тороидальное. Значит, подход Брагинского дает возможность получения замкнутого динамо-цикла: полоидальное поле превращается в тороидальное и обратно. Подход Штейнбека, Краузе и Редлера является более общим. Для той же цели, что Паркер и Брагинский, они используют турбулентную (т. е. хаотическую) конвекцию, присущую подфотосферному слою Солнца, которая отличается отсутствием зеркальной симметрии. Эта работа получила особенно широкую известность и развитие в более поздних динамо-моделях солнечных циклов, явившихся предметом обсуждения специально-го симпозиума Международного астрономического союза в Праге в 1975 г. «Основные механизмы солнечной активности». Все динамо-модели, начиная с построенных Бэбкоком и Лейтоном, являются кинематическими, т. е. для них безразлично, откуда взялся тот или иной тип движения и магнитного поля (все эти характеристики считаются заданными).

Итак, практически все модели гидромагнитного солнечного динамо держатся на «двух китах»: дифференциальном вращении и турбулентной конвекции. Но имеется еще одна сторона в моделях подобного рода, которая оказывается самой уязвимой. Дело в том, что создать нужное магнитное поле и внести его в солнечную атмосферу оказывается гораздо легче, чем избавиться от его излишков. Ведь обычно в космических условиях из-за громадных характерных размеров магнитное поле удерживается в лучшем случае не меньше сотни лет. Поэтому вместо обычной диффузии, привычной для классической электродинамики, приходится вводить турбулентную диффузию. Вычисление ее коэффициента базируется на теории случайных процессов, и поэтому как только речь заходит о турбулентной диффузии, так сразу же доказательство уступает свое место как бы символу веры (лучше сказать, доверия или уверенности, но это не меняет дела). Но так или иначе только этим способом динамо-модель позволяет за нужное время избавиться от избыточного магнитного поля.

Как уже, вероятно, понял читатель, исходное полоидальное магнитное поле в динамо-теориях солнечных циклов принимается сравнительно слабым, с напряженностью во всяком случае не выше сотен гаусс. Именно поэтому движения могут диктовать этому полю в конвективной зоне Солнца свою волю. Очень важен для динамо-моделей вопрос о характере изменения угловой скорости вращения с глубиной в подфотосферной конвективной зоне, т. е. о знаке радиального градиента угловой скорости и о соотношении его с широтным градиентом этой скорости. Почти во всех современных моделях подобного рода его принимают отрицательным. Однако в некоторых из них знак этого градиента изменяется внутри конвективной зоны.

Было бы наивным и определенно излишним пытаться заинтересовать широкого читателя всем обилием решений магнитогидродинамических уравнений, которые занимают доминирующее место в работах по теории гидромагнитного динамо. Это скорее вопросы прикладной математики (поскольку чаще всего решения получены численными методами), чем физики Солнца, тем более, что все эти численные эксперименты, как называют их сами авторы динамо-моделей, интересны не столько способом их проведения, сколько их результатами. Вот на этих результатах мы и сосредоточим свое внимание. Заметим лишь, что решение уравнений, как правило, в таких исследованиях проводилось в линейном приближении. Только буквально в самые последние годы появились работы, учитывающие так называемые нелинейные эффекты, суть которых сводится к обратному воздействию магнитного поля на движения.

Как показали численные эксперименты, наиболее удовлетворительное согласие теории с наблюдениями получается, если помимо изменения угловой скорости вращения Солнца с широтой учитывать также изменение ее с глубиной, хотя и сравнительно медленное. В результате получаются две ветви динамоволны, начинающиеся на средних широтах и смещающиеся к полюсу и к экватору. Следует иметь в виду, что радиальный градиент угловой скорости уменьшает тороидальное поле и увеличивает полоидалыюе. Тем самым он как бы автоматически учитывает полоидальные поля несколько более сильные и активные на полярной ветви, чем на экваториальной, в согласии с наблюдениями. Магнитная активность, возникающая на высоких широтах примерно за год до появления первых пятен нового цикла, является прямым продуктом экваториальною ускорения Солнца. Радиальный же градиент угловой скорости его вращения частично подавляет развитие полярной ветви. В то же время основные магнитные поля, возникающие на средних широтах и от них мигрирующие к экватору и полюсу, представляют собой главным образом продукт радиального градиента угловой скорости. Итак, детали подфотосферного вращения Солнца прямо отражаются на поведении поверхностных магнитных полей. Имеются веские основания считать источник солнечной активности расположенным в нижней части конвективной зоны, на глубине не меньше 200 000 км. Более того, даже эта глубина кажется маловатой для обеспечения соизмеримости с временными характеристиками 11-летнего цикла. И тут на помощь нам приходит недавно открытый диамагнитный эффект конвективной зоны, суть которого сводится к смещению магнитных силовых линий к дну этого подфотосферного слоя. Характерное время этого смещения равно примерно одному году и не зависит от напряженности поля.

Модели линейного гидромагнитного солнечного динамо объясняют только основные особенности 11-летнего и 22-летнего циклов солнечной активности: периодичность в изменении полярности магнитного поля полярных и близэкваторнальных областей Солнца и смещение максимумов этого поля по широте, фазовые соотношения между полоидальной и тороидальной составляющими поля. Это не так мало. Естественно было бы ожидать от них также объяснения и более длинных солнечных циклов, а также и возможных нерегулярных долговременных изменений уровня солнечной активности. Но это под силу только нелинейным динамо-теориям. Путь к решению этой задачи лежит через изучение нелинейного обратного воздействия магнитного поля на генерирующие его движения. Хотя такие исследования находятся еще, можно сказать, в младенческом возрасте, они уже дали самое главное, что от них можно было ожидать. А именно, оказалось, что если такой механизм нелинейного обратного воздействия на систему «дифференциальное поле - крупномасштабная конвекция» действительно работает, тогда солнечное динамо должно испытывать модуляцию, связанную с солнечным циклом. Прежде всего ом приводит к модуляции 80 - 90-летнего или 55-летнего циклов, причем сохраняется устойчивое 11-летнее колебание магнитного поля. Кроме того, в результате этого обратного воздействия может происходить сильное ослабление крупномасштабной конвекции, которое приведет к резкому понижению уровня солнечной активности, характерному для продолжительных ее минимумов типа маундеровского. Заметим, что недавно было выдвинуто еще одно любопытное объяснение солнечных минимумов подобного рода, согласно которому их появление связано с перестройкой типа крупномасштабной конвекции от меридионального к широтному. На этом нам придется поставить точку, хотя именно в этой области сейчас следует ожидать наибольшего продвижения вперед динамо-теорий солнечной цикличности.

Вы, наверное, уже обратили внимание на то, что здесь ни единого слова не было сказано об объяснении существования активных долгот. Это невозможно сделать даже с помощью моделей нелинейного осесимметричного гидромагнитного солнечного динамо. Для этого требуются неосесимметричные решения уравнений Динамо. Пока в данном направлении предприняты только первые, хотя и обнадеживающие шаги. Но здесь предстоит еще очень большая работа.