Что такое трасса полета спутника

Открыв планшет, штурман самолета может похвастаться: вот маршрут предстоящего полета. Баллистикам, конечно, завидно, что летчики столь эффектно и наглядно могут изобразить свой путь. И они стали думать, а нельзя ли нечто аналогичное отыскать и для описания полета космического аппарата? В результате был найден удобный способ отразить характер движения спутника относительно Земли точно на таких же картах, какие используются в авиации. И, наверное, в честь этого достижения в одной песне о космонавтах появились слова: "Заправлены в планшеты космические карты"... Правда, относительно последующей строки песни "И штурман уточняет в последний раз маршрут" с автором ее следует поговорить особо. Вы ведь уже знаете, что уточнить маршрут - это значит как-то изменить начальные условия движения. Они, в свою очередь, находятся специалистами-баллистиками в результате длительных трудоемких вычислительных работ с использованием совершеннейших электронных вычислительных машин с учетом всех возможностей ракеты и требований программы полета. Вот поэтому штурман непосредственно перед стартом ("...Ведь нам еще осталось 14 минут") практически не сможет уточнить "в последний раз маршрут".

Маршрут движения космического аппарата относительно Земли баллистики назвали звучным словом трасса.

Трассой полета спутника называется проекция его орбиты на поверхность Земли. Построение ее производится следующим образом. Для каждого заданного момента времени рассчитывается прогноз движения спутника, т. е. определяются его координаты. Затем точка, где находится спутник, соединяется прямой линией с центром Земли. Точка пересечения этой прямой с поверхностью Земли называется подспутниковой точкой.

Построив для ряда моментов времени подспутниковые точки и соединив их плавной кривой, получим трассу движения.

Можно изготовить простую механическую модель спутника для вычерчивания трассы спутника. Для этого возьмите обыкновенный школьный глобус Земли и рядом с ним укрепите жесткий металлический обруч так, чтобы глобус находился внутри обруча, а центры обруча и глобуса совпадали (рис. 22). Глобус будет как бы изображать вращающуюся Землю, а обруч - круговую орбиту. Теперь приложите карандаш к обручу так, чтобы острие его касалось глобуса и было направлено к его центру. Передвигая карандаш вдоль обруча, вы будете как бы изображать полет спутника. Если одновременно вращать глобус (моделируя вращение Земли), то карандаш оставит на глобусе плавную кривую, которая и будет изображать след спутника. Трасса будет тем точнее, чем лучше вы выдержите соотношение периодов вращения Земли и обращения спутника.

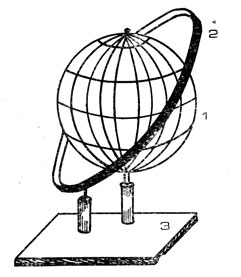
Рис. 22. Механическая модель для вычерчивания трассы кругового спутника: 1 - глобус; 2 - металлический обруч; 3 - подставка

Модель движения спутника относительно Земли можно, разумеется, значительно усовершенствовать и отражать на ней полет спутника в естественном темпе времени. Для этой цели можно применить автоматическую систему синхронизации вращения глобуса с земным и перемещение макета спутника по поверхности глобуса - с действительным полетом его относительно Земли. Тогда положение макета на глобусе на каждый момент времени будет в точности соответствовать координатам летящего корабля. Такое устройство применялось при запуске первых искусственных спутников Земли и было до поры до времени предметом восхищения журналистов. Однако этот глобус, устанавливаемый ранее в координационно-вычислительном центре, уже свое отслужил. Вместо глобуса появился огромный матовый световой экран с картой Земли. По карте ползет светящееся пятнышко, направляемое специальным электронным счетным устройством. Это пятнышко изображает собой летящий космический корабль. На той же карте определенными значками нанесены наземные измерительные пункты и зоны их радиовидимости в виде овалов. Когда "зайчик" входит в очередной овал, то это означает, что данный измерительный пункт "видит" летящий корабль и, стало быть, может держать с ним связь.

Но, изжив себя в координационно-вычислительном центре, глобус остается пока еще незаменимым помощником космонавтов. Его устанавливают на борту, в кабине космонавтов. Для них глобус является очень удобным и важным прибором, помогающим ориентироваться в полете и распознавать географические "черты" Земли. Такой глобус часто называют навигационным и он применяется на кораблях-спутниках "Восток", "Восход", "Союз".

Научившись строить трассы полета спутников на глобусе или на карте, теперь можно рассмотреть вопрос о том, как они выглядят и какие элементы орбиты можно определить с их помощью.

Начнем с простейшего случая построения трассы стационарного спутника Земли. Пусть этот спутник движется по экваториальной орбите. Радиус орбиты его может быть найден из условия: период обращения спутника должен быть равен одним звездным суткам (т. е. времени, в течение которого Земля совершает относительно звезд один полный оборот вокруг своей оси). Вычисления показывают, что радиус орбиты спутника должен быть равен 35809 км. Иначе говоря, спутник будет летать на высоте 29438 км со скоростью 3076 м/сек. При движении по стационарной экваториальной орбите он будет как бы висеть над одной и той же точкой поверхности Земли, расположенной на ее экваторе. Трасса спутника изобразится чрезвычайно просто: точка на карге. Вот вам и весь "маршрут" движения! Конечно, это обстоятельство может дать пищу для иронии не только летчикам или морякам, но даже пешеходам, которые, хотя и медленно, но все же перемещаются относительно поверхности Земли. Однако баллистики вместе с астрономами могут ответить им: природе далеко не безразличны стационарные орбиты, ведь Земля по отношению к Луне является своеобразным стационарным "спутником". Светлый лик Луны всегда обращен к Земле одной и той же стороной, а Земля, образно говоря, висит над неизменной областью поверхности Луны. И только благодаря старанию людей, создавших межпланетную станцию "Луна-3", удалось заглянуть за скрытую от Земли часть Луны, покинув стационарную орбиту. Если радиус орбиты спутника меньше радиуса стационарной орбиты, то период обращения его уменьшится, т. е. он совершит один виток быстрее, чем обернется Земля. Трасса полета спутника будет совпадать с экватором Земли, а подспутниковая точка "станет перемещаться вдоль него с запада на восток (в направлении вращения Земли). Наоборот, когда спутник выведен на орбиту радиус которой превысит радиус стационарной орбиты, то в своем движении он будет отставать от вращения Земли и подспутниковая точка будет перемещаться вдоль экватора с востока на запад в направлении, обратном вращению Земли.

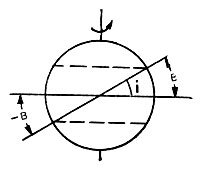
Рис. 23. Образование трассы спутника на поверхности Земли. Вся трасса умещается в полосе, не выходящей за широту ±В от экватора

А как будет выглядеть трасса если плоскость орбиты спутника не будет совпадать с плоскостью экватора? Чтобы разобраться в этом, обратимся к рис. 23. На нем схематически показана Земля и орбита спутника, если на нее смотреть с "ребра". Отсюда непосредственно видно, что наибольшая широта точек трассы будет численно равна наклонению плоскости орбиты. Таким образом, трасса круговой орбиты спутника Земли на карте Земли будет располагаться в полосе между параллелями, отстоящими от экватора к северу и к югу на угол, равный наклонению плоскости орбиты. Значит, если дана трасса полета спутника по круговой орбите, то на ней вы можете найти широту наиболее удаленной от экватора точки трассы и она численно будет равна наклонению плоскости орбиты к экватору.

Рассмотрим теперь движение спутника с момента времени, когда он пересек экватор при переходе с южного полушария к северному (как известно, подспутниковая точка в этот момент будет соответствовать положению восходящего узла орбиты). За время одного оборота спутника по орбите, т. е. к моменту прихода его к экватору, Земля провернется на некоторый угол, величина которого будет зависеть от периода обращения спутника. Этот угол, отсчитываемый вдоль экватора, баллистики называют смещением спутника по долготе за виток орбиты (для краткости иногда говорят - смещение за виток). Для кругового спутника Земли при высоте орбиты 200 км величина смещения будет составлять 22°. При увеличении радиуса орбиты величина смещения за виток будет также возрастать и для стационарных спутников она достигнет 24 часа звездных.

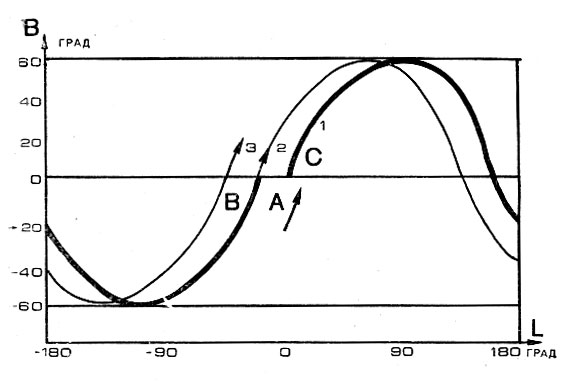
Рис. 24. Трасса полета спутника при движении по круговой орбите с наклонением 60° (первые два витка): В - широта; L - долгота

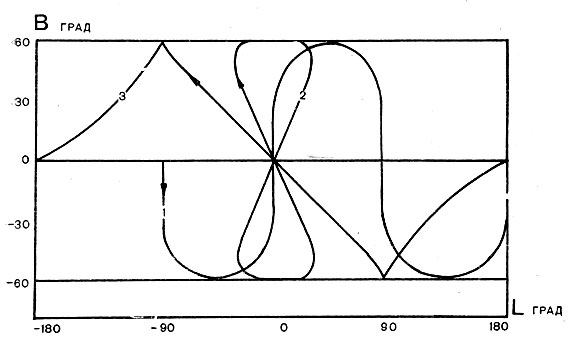
Рис. 25. Трассы полета спутников с наклонением 60° и смещением по долготе за один виток 180° (1), 360° (2) и 720° (3)

Примеры различных трасс спутников изображены на рис. 24, 25. По горизонтальным осям рисунков отложена долгота проекции спутника на земную поверхность, а по вертикальным - широта. На этих рисунках отчетливо видно, что трасса спутника всегда проходит в полосе между двумя .параллелями, симметричными относительно экватора.

Рассмотрим более подробно рис. 24. Жирная линия на нем изображает трассу полета спутника на первом витке. Начиная ют экватора (точка А), трасса поднимается в северное полушарие и, коснувшись параллели, уходит снова к экватору, пересекает его, затем подходит к южной параллели, касается ее и снова подходит к экватору со стороны южного полушария (точка В). Расстояние между точками А и В и есть смещение спутника по долготе за виток. Последующие витки трассы могут быть получены путем последовательного смещения се от витка к витку на величину отрезка АВ. Для облегчения рисования трассы можно изготовить специальное лекало.

Очевидно, что если смещение за виток укладывается целое число раз в длине экватора Земли, то трасса спутника через определенное число витков подойдет к точке А и в последующем будет повторяться.

Пусть N есть ближайшее целое число витков, которое спутник совершает приблизительно за сутки. Если после завершения N витков спутник не выйдет в точку А, а окажется, например, в точке С, то угловое расстояние по долготе между точками Л и С называют суточным смещением орбиты. Когда это смещение равно нулю, то спутник через сутки возвратится в исходное положение.

Исходя из описанных особенностей движения спутника Земли, мы теперь можем со знанием дела дать комментарии к следующим сообщениям ТАСС:

"Сегодня, 11 октября, в 14 часов 10 минут московского времени в Советском Союзе стартовала ракета-носитель с космическим кораблем "Союз-6". В 14 часов 19 минут корабль "Союз-6" с высокой точностью выведен на расчетную орбиту спутника Земли... По данным траекторных измерений параметры орбиты корабля следующие:

- максимальное расстояние от поверхности Земли (в апогее) 223 километра;

- минимальное расстояние от поверхности Земли (в перигее) 186 километров;

- наклонение орбиты 51,7 градуса;

- период обращения вокруг Земли 88,36 минуты "... " Продолжая намеченную программу научно-технических исследований и экспериментов кораблей "Союз", 12 октября 1969 года в 13 часов 45 минут московского времени в Советском Союзе произведен запуск второго космического корабля - "Союз-7"... Экипажи кораблей "Союз-6" и "Союз-7" установили между собой надежную двустороннюю радиосвязь".

В последующих сообщениях ТАСС говорилось, что параметры орбиты корабля "Союз-7" близки к параметрам орбиты корабля "Союз-6".

Прочитав внимательно эти сообщения ТАСС, давайте попробуем объяснить вопрос, почему старт корабля "Союз-7" произведен в 13 часов 45 минут? Можно предполагать, что время старта корабля "Союз-7" выбиралось из условия, чтобы после выведения на орбиту он оказался как можно ближе к кораблю "Союз-6" (..."установили между собой надежную двустороннюю радиосвязь"...). Для этого, очевидно, необходимо, чтобы трасса корабля "Союз-6" проходила через точку старта корабля "Союз-7". Проверим нашу гипотезу. Из сообщения ТАСС находим, что старт корабля "Союз-7" произведен спустя 23 часа 26 мин после старта корабля "Союз-6". При периоде обращения корабля "Союз-6" 88,36 мин в промежуток времени 23 час 26 мин. укладывается почти (без нескольких минут) 16 витков его вокруг Земли. Расхождение в несколько минут можно объяснить влиянием нецентральности тюля сил на полет корабля. Отсюда следует, что трасса корабля "Союз-6" действительно проходила в окрестности точки старта корабля "Союз-7" и тем самым обеспечивался их последующий близкий полет.

Изменение периода обращения спутника существенно меняет вид трассы его полета. В этом вы можете убедиться, еще раз посмотрев на рис. 25. Особый интерес представляет собой трасса полета стационарного спутника, плоскость орбиты которого не совпадает с плоскостью экватора. Из рис. 25 видно, что трасса спутника представляется в виде "восьмерки", расположенной над одним и тем же районом земной поверхности. Она "сужается" с уменьшением наклонения и стягивается в точку, когда орбита становится экваториальной.

Таким образом, мы рассмотрели основные характеристики движения кругового спутника относительно вращающейся Земли. Существенно отметить, что трасса его или "маршрут" движения не могут быть нарисованы произвольно, как это, скажем, выполняется при назначении маршрута полета самолета. Трасса спутника, несмотря на ее причудливый вид, отвечает строгим закономерностям движения и не может быть изменена произвольным образом. Она целиком и полностью определяется наклонением плоскости орбиты и периодом обращения спутника.