Полет с переменной скоростью

Основная характеристика кругового движения - полет с постоянной скоростью. Создать круговую орбиту - это значит вывести космический аппарат на строго заданную высоту при точно отмеренной величине скорости и направлении полета. Из-за ошибок системы управления ракеты-носителя, а также отличия поля Земли от центрального образовать чисто круговое движение практически невозможно. Естественно возникает вопрос, а по какой орбите полетит космический аппарат, если скорость его окажется отличной от круговой или, оставаясь равной круговой, будет направлена иначе? На этот вопрос отвечает теория эллиптического движения. Орбита полета в пределах ограниченного изменения скорости по сравнению с круговой станет эллиптической.

Полет по эллиптической орбите не имеет столь простых аналогий, как круговое движение. Чтобы разобраться в его особенностях, нам придется привлечь один из фундаментальных законов механики - закон сохранения энергии. Применительно для случая движения космического аппарата в центральном поле сил он может быть сформулирован следующим образом: сумма кинетической и потенциальной энергий космического аппарата есть величина постоянная. Символически этот закон можно записать в форме:

кинетическая энергия + потенциальная энергия = постоянная величина 

Конечно, этот закон имеет строгое математическое выражение. Но для последующего качественного анализа нам достаточно его символической формы записи.

Дадим несколько пояснений к написанному закону.

Потенциальная энергия - это энергия поднятого над Землей тела; она проявляется в виде механической работы, которую можно совершить при опускании тела на Землю. Простейшая количественная мера этого вида энергии - это произведение веса тела на поднятую высоту. Запас потенциальной энергии изменяется, когда вы поднимаетесь вверх по лестнице или достигаете заоблачных высот вместе с самолетом. Чем выше вы поднялись, тем больше запас энергии, и, наоборот, с понижением высоты ее количество уменьшается. Однако не следует путать потенциальную энергию с истинным смыслом слов "потенциальные возможности". Например, потенциальные возможности металлургического комбината заключаются, конечно, не в том, что его построили на высокой горе, а в его возможности увеличить выплавку количества металла. Кинетическая энергия - это энергия механического движения. Мерой ее служит величина, точнее, квадрат скорости перемещения. Чем больше скорость, тем больше кинетическая энергия.

Когда самолет на взлете увеличивает скорость своего движения, то кинетическая энергия его возрастает. После взлета, совершая полет с постоянной скоростью и набором высоты, самолет будет увеличивать свою потенциальную энергию при. неизменной кинетической энергии.

Два указанных вида энергии могут переходить друг в друга/ Поднятый над землей камень обладает определенным запасом потенциальной энергии. Если его опустить, то он, падая, будет увеличивать свою скорость и уменьшать высоту, т. е. будет осуществляться переход потенциальной энергии в кинетическую. Но существенным будет то, что суммарное количество ее в любой момент падения остается неизменным.

Когда космический аппарат выведен на орбиту и в дальнейшем совершает пассивный полет, он имеет строго определенный запас механической энергии, количество которой в соответствии с законом сохранения энергии остается неизменным в течение всего времени полета (необходимо отметить, что мы рассматриваем случай движения в центральном поле сил). При полете по круговой орбите, т. е. при постоянном расстоянии от центра планеты и неизменной скорости, потенциальная и кинетическая энергии космического аппарата не меняются в процессе полета. В случае движения по эллиптической орбите высота полета периодически, через каждый виток, колеблется от некоторого минимального значения (в перигее) до максимального (в апогее). Соответственно с изменением высоты будет изменяться потенциальная энергия космического аппарата. Но так как механическая энергия должна оставаться одной и той же, то изменение высоты полета приведет к автоматическому изменению кинетической энергии. Это, в свою очередь, выразится в увеличении или уменьшении скорости полета. Происходит своеобразная перекачка потенциальной энергии в кинетическую и наоборот. В перигее, где высота полета минимальна, кинетическая энергия достигает наибольшего значения и, значит, скорость полета станет также максимальной. В то же время скорость полета в апогее будет минимальна. Таким образом, полет по эллиптической орбите сопровождается непрерывным периодическим от витка к витку изменением величины и направления скорости, а также высоты полета. В этом состоит внешнее отличие эллиптической орбиты от круговой. Круговое движение является частным случаем эллиптического: эллипс превращается в круг при равных высотах перигея и апогея.

При малых отличиях высот апогея и перигея орбита космического аппарата внешне будет похожа на окружность и в ряде случаев мы не сможем отличить их на рисунке. Когда эллиптическая орбита достаточно мало отличается от круговой, то случай движения по таким орбитам обычно называют почти круговым. О нем мы уже упоминали ранее. Смысл введения почти кругового движения не случаен. Оказывается, что движение по таким орбитам можно достаточно точно описать с помощью простых математических зависимостей, дающих возможность рассчитать поправки к опорному круговому движению. Этот аппарат разработан достаточно подробно и мы к нему будем неоднократно обращаться.

Таким образом, почти круговое движение может быть описано с помощью следующей символической формулы

почти круговое движение = круговое движение + малые поправки

Теперь мы можем рассмотреть некоторые качественные задачи, иллюстрирующие взаимное геометрическое положение круговых и эллиптических орбит.

Задача 1. Космический аппарат совершает полет по круговой орбите. Какой вид примет его орбита, если скорость полета увеличить на некоторую малую величину?

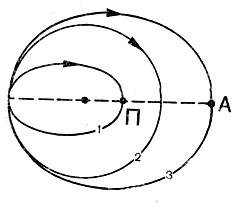
Рис. 26. Круговая (2) и эллиптическая (1,3) орбиты

Мы уже знаем, что при движении по круговой орбите центробежная сила уравновешивается силой притяжения Земли. Когда произойдет увеличение скорости полета, то это равновесие сил нарушится, поскольку центробежная сила, зависящая от скорости, увеличится. За счет воздействия этой силы космический аппарат начнет уходить во внешнюю сторону от круговой орбиты (рис. 26). Однако после этого направление скорости полета не будет перпендикулярным радиусу-вектору. -Следовательно, какая-то часть силы притяжения Земли пойдет на затормаживание движения космического аппарата, т. е. уменьшение его скорости, с одновременным поворотом вектора скорости к Земле. Процесс затормаживания будет продолжаться до момента достижения апогея орбиты. В тот момент скорость полета станет наименьшей, но перпендикулярной радиусу-вектору. После прохождения апогея составляющая силы притяжения начнет уже разгонять космический аппарат, приближая его к Земле. К моменту завершения витка космический аппарат вернется в первоначальную точку с той же самой скоростью, с которой он отлетал из нее. Таким образом, после увеличения скорости орбита движения станет эллиптической, целиком охватывающей начальную круговую орбиту.

Задача 2. Космический аппарат совершает полет по круговой орбите. Что произойдет с орбитой, если скорость полета его уменьшить на небольшую величину?

Здесь равновесие сил изменится в противоположном направлении: после уменьшения скорости сила притяжения станет преобладать над центробежной, и космический аппарат изменит свою траекторию полета внутрь круговjй орбиты (рис. 26). Далее полет будет происходить с нарастанием скорости, а после прохождения перигея - с уменьшением ее. После завершения витка космический аппарат возвращается в исходное состояние. Таким образом, в результате уменьшения круговой скорости орбита космического аппарата становится эллиптической, лежащей внутри круговой.

Обратим ваше внимание на одно любопытное обстоятельство. Когда при полете по круговой орбите производилось увеличение скорости, то в противоположной точке эллиптической орбиты наблюдалось ее уменьшение, и наоборот. Этот парадоксальный эффект находит широкое применение при решении вопросов маневрирования космических аппаратов и подробным образом будет рассмотрен ниже.

Изложенные рассуждения показывают, что эллиптическая орбита является удобной "дорогой", дающей возможность от окраины Земли подниматься на громадные высоты и "бесплатно" возвращаться обратно. В связи с этим у любознательного читателя может возникнуть вопрос: а на какую величину изменится высота полета космического аппарата, если при полете по круговой или почти круговой орбите скорость его увеличить или уменьшить, скажем, на 1 м/сек? Ответ на этот вопрос даст следующая приближенная формула, справедливая для орбит спутников Земли с высотой 200 - 600 км:

h = 3,8 ΔV км?

где h - изменение высоты полета, ΔV - изменение скорости полета, выраженное в м/сек. Из этой формулы следует, что если скорость полета увеличить всего на 1 м/сек, то космический аппарат перейдет на эллиптическую орбиту, апогей которой будет на 3,8 км выше начальной орбиты. Наоборот, уменьшение скорости полета на 1 м/сек приведет к тому, что орбита в перигее понизится на 3,8 км. Эти результаты свидетельствуют о значительной "чувствительности" размеров эллипса к изменению скорости движения по начальной орбите. Бегуны-спринтеры на ближних дистанциях развивают скорость до 10 м/сек, но, очевидно, мало чего меняют в своем пространственном положении. Если же на эту величину изменить скорость спутника Земли, то он "подскочит" почти на 40 км. В этом смысле космос более чувствителен к установлению рекордов.

Задача 3. Как будет выглядеть взаимное положение круговой и эллиптической орбит при равных периодах обращения?

Для решения этой задачи нам необходимо обратиться к математике. Ранее было установлено, что период обращения космического аппарата, совершающего полет по круговой орбите, может быть найден по формуле

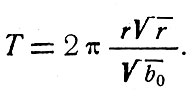
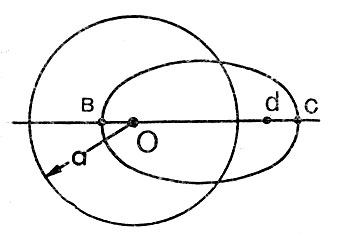
Рис. 27. Схема построения эллиптической орбиты, период обращения по которой равен периоду обращения при движении по круговой орбите заданного радиуса

Аналогичная формула для периода обращения по эллиптической орбите будет иметь вид

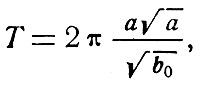
где а - большая полуось. Отсюда следует, что периоды обращения по круговой и эллиптической орбите будут одинаковыми, если а = r, т. е. большая полуось эллиптической орбиты равна радиусу круговой орбиты. Полученное соотношение ничего не говорит о величине эксцентриситета орбиты, т. е. он может быть любым. Значит, форма эллиптической орбиты при одном и том же периоде обращения может быть и почти круговой, и сильно вытянутой при одном ограничении, чтобы большая полуось ее оставалась постоянной. Но большая полуось связана с радиусами перигея и апогея следующим простым соотношением

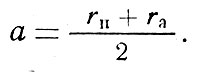
Отсюда следует простой способ построения орбит с одинаковыми периодами обращения:

- начертить окружность радиуса а (рис. 27);

- через центр окружности О провести прямую линию;

- на этой прямой произвольным образом отложить отрезок bс, равный диаметру окружности, так, чтобы центр окружности оказался где-либо внутри отрезка;

- от наиболее удаленного конца отрезка (точка с) в сторону центра окружности отложить дугой отрезок cd = Ob.

В результате построения получаем: отрезок Ob - радиус: перигея, отрезок О_с - радиус апогея, точки O, d - фокусы эллипса. Для построения эллипса необходимо взять нить, длина которой равна диаметру окружности, и концы ее укрепить в фокусах эллипса.

Из приведенных рассуждений следует, что круговая и эллиптическая орбиты, периоды обращения по которым равны, всегда пересекаются друг с другом. Если на чертеже даны рзп; круговых и эллиптических орбит, то, измерив их диаметры, вы всегда найдете орбиты с равными, наибольшими или наименьшими периодами обращения: равным диаметрам будет соответствовать одинаковый период обращения и большим диаметрам - больший период обращения.

Задача 4. После выведения на орбиту ракета-носитель сообщила космическому аппарату заданную по величине скорость полета, но направление ее отклонилось на некоторый угол в плоскости орбиты. Какую форму будет иметь новая орбита?

Так как вектор скорости полета космического аппарата после выведения на орбиту наклонен под некоторым углом к горизонту, то полученная орбита будет эллиптической, поскольку в круговом движении вектор скорости полета всегда параллелен горизонту. Конечно, всегда будет интересно знать, а на сколько новая орбита будет отличаться от круговой, если известна величина угла отклонения скорости. Для приближенной оценки изменения высоты полета в зависимости от величины утла отклонения вектора скорости можно воспользоваться следующей формулой:

h = 115 α км,

где угол α должен быть подставлен в градусах. Эту формулу можно применять для орбит спутников Земли с высотой полета от 200 до 600 км. Если, например, угол отклонения вектора тяги составляет 1^о, то получим h = 115 км. Найденный результат необходимо понимать так: высота полета спутника по отношению к первоначальной круговой орбите в одной точке орбиты увеличится на 115 км, а в противоположной ей - уменьшится на 115 км. Иначе говоря, если первоначальная орбита была круговой с высотой, например, 300 км, то новая орбита станет эллиптической с высотой апогея 415 км и высотой перигея 185 км. Эта же формула применима для расчета изменения высоты полета и в том случае, когда первоначальная орбита была почти круговой.

Приведенные результаты показывают, что большое отклонение направления скорости спутника может грозить серьезной опасностью. Например, если при выведении на орбиту с высотой 200 км допущено завышение угла всего на половину градуса, то это приведет уже на первом витке вначале к повышению высоты полета до 267 км, а затем к понижению ее до 133 км. Как уже упоминалось, за счет сильного тормозящего влияния атмосферы спутник не может продолжать полет по орбите и поэтому он упадет на Землю. Эти простые рассуждения со всей очевидностью свидетельствуют о том, какая исключительно высокая точность требуется от системы управления выведением ракеты-носителя.

В качестве примера произведем оценку наибольшей величины отклонения направления скорости полета спутников Земле. 6 августа 1961 года в 9 часов по московскому времени в орбитальный полет стартовал второй космический корабль "Восток-2" с летчиком-космонавтом Германом Степановичем Титовым. Корабль выведен на орбиту с высотой в апогее 244 км и в перигее 183 км.

В книге "700000 километров в космосе" Герман Степанович Титов пишет:

"Я чувствовал отделение каждой ступени ракеты, уносившей корабль все выше и выше к расчетной орбите. Хронометр показывал, что "Восток-2" вот-вот выйдет на нее. В этот момент должно возникнуть состояние невесомости, и я приготовился к нему. Но оно возникло плавно, само собой, после отделения последней ступени ракеты".

Итак, корабль "Восток-2" вышел на орбиту. Система управления ракетой, конечно, не могла работать идеально и "совершила" некоторые ошибки. Оценим порядок величины ошибки по выдерживанию направления скорости полета. Давайте предположим наихудший случай: корабль "Восток-2" должен быть выведен на круговую орбиту со средней высотой полета

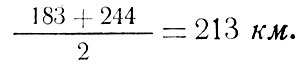
Тогда па долю системы .управления падает ошибка в высоте, равная 244 - 213 = 31 км. А это означает, что если вся эта ошибка возникла только за счет отклонения вектора скорости от расчетного направления, то величина угла отклонения не будет превышать 0,3 градуса. При этом необходимо подчеркнуть: всю ошибку в высоте орбиты мы отнесли целиком только к отклонению направления скорости, не учитывая влияния других ошибок и возмущений. А они ведь тоже "участвовали" в искажении орбиты и поэтому ошибка ориентации вектора тяги наверняка будет меньше полученной для нее величины.