8. Определение химического состава туманностей

Если известны температура и эффективные сечения возбуждения, то по относительным интенсивностям небулярных и водородных линий можно вычислить содержание соответствующих ионов в туманности. Действительно, число возбуждений на второй уровень электронным ударом

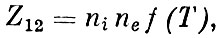
Формула электронного удара

где n_i- число ионов в 1 см³, f(T) - некоторая функция, включающая эффективное сечение и долю быстрых электронов, способных возбудить данный ион. Если удары второго рода несущественны, то Z₁₂ почти равно числу излучаемых квантов линий, в противном случае нужно внести определенные поправки. Как было показано выше) излучение в бальмеровских линиях пропорционально n_e² и слабо зависит от температуры. Поделив выражения для интенсивностей, найдем, что ^n_i/_nе пропорционально отношению интенсивностей небулярной и бальмеровской линий, которое может быть найдено из наблюдений, причем коэффициент пропорциональности - известная функция температуры и плотности (плотность входит только в множитель, учитывающий удары второго рода).

Так было вычислено относительное содержание О III, О II, N II, S II, Ne III, Ne IV, Ne V, A III, A IV, A V и других ионов. В некоторых случаях использовались и линии типа полярных сияний. Содержание этих ионов еще не дает химического состава, так как часть атомов может находиться в других состояниях ионизации, не дающих линий в видимой области спектра. Нужно как-то оценить долю этих "невидимых" атомов. Если бы спектр излучения звезды был подобен спектру излучения черного тела в широком участке спектра, включающем области, ответственны за ионизацию ионов (от 1000 до 100 А), то возможно было бы теоретически рассчитать степень ионизации элементов. Тогда по концентрации ионов одного сорта можно было бы определить концентрации других ионов того же элемента, и сложив их, найти содержание данного элемента вообще. К сожалению, теоретический расчет не дает удовлетворительных результатов, так как, во-первых, излучение звезды в ультрафиолетовой области сильно отличается от излучения черного тела, а во-вторых, проходя через туманность, оно поглощается, причем в разных частях спектра по-разному. Несколько более надежен, хотя далеко не безупречен, другой, полуэмпирический метод. Делается предположение, что в данной туманности степень ионизации разных ионов зависит только от энергии, необходимой для отрыва электрона. Тогда можно построить график этой зависимости, используя данные о содержании разных ионов. Среди ионов, концентрация которых известна, можно выделить такие пары, как О II и О III, Ne III и Ne IV, Ne IV и Ne V и т. д. По ним строится график, в котором абсциссой служит энергия ионизации первого члена пары, а ординатой - отношение их концентраций. Каждая пара ионов дает на графике одну точку, все они вместе определяют некоторую кривую. Пользуясь этой кривой, можно по содержанию какого-либо иона оценить содержание ионов того же элемента в смежных стадиях ионизации и таким образом найти полное содержание элемента. Подобный анализ был ранее проведен для ряда туманностей Л. Адлером и Д. Мензелом (США), а недавно Л. Адлер выполнил детально такие же расчеты для планетарной туманности NGG 7027, используя новые данные об интенсивностях линий и об эффективных сечениях. Ниже приводятся логарифмы относительных чисел атомов в этой туманности. Для сравнения приведен также средний химический состав звезд. Все числа атомов даны в сравнении с кислородом, для которого логарифм относительного содержания принят за 10,00.

Логарифмы относительных чисел атомов разных элементов в NGC 7027 и в нормальных звездах (по Адлеру)

^* (Двоеточие означает малую точность оценки)

Хотя у некоторых элементов различие и кажется значительным, однако оно все же не превышает возможных ошибок, учитывая ненадежность значений температуры, эффективных сечений, отклонение ионизации разных элементов от значений, выведенных из средней зависимости, и т. д. Немалую роль в увеличении ошибок играют неоднородности в распределении плотности, температуры и ионизации в туманности. Поэтому можно считать, что отличие химического состава туманности и звезд не превышает возможной неточности расчета. Этот результат имеет, разумеется, большое принципиальное значение.