Телескоп - рефрактор

Наиболее простая конструкция телескопа для наблюдения Солнца - это рефрактор. В простейшем случае его оптическая схема такая же, как у фотоаппарата: объектив, в фокальной плоскости которого строится изображение Солнца (см. рис. 1). Но, если мы вспомним, что фокусное расстояние объектива в 100 раз больше диаметра получаемого с его помощью изображения Солнца, то легко понять, что нужно иметь очень длинную трубу, чтобы можно было рассмотреть изображение Солнца или его фотоснимок. На практике телескоп-рефрактор всегда содержит второй объектив-окуляр, позволяющий построить увеличенное изображение без существенного увеличения габаритов телескопа. При наблюдениях звезд окуляр часто служит для рассматривания изображения участка неба или отдельного небесного объекта. В этом случае существенна такая характеристика телескопа, как увеличение. Оно определяется отнощением утла, под которым выходят световые пучки из окуляра, к углу, под которым они падали на объектив. Это отношение можно выразить через фокусные расстояния объектива F и окуляра f:

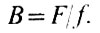
На Солнце нельзя смотреть через окуляр - можно сжечь глаза.

Поэтому мы рассмотрим только вариант схемы, в которой при помощи окуляра строится увеличенное (по отношению к размеру в фокальной плоскости объектива) изображение Солнца. Оптическая схема окулярной части телескопа - рефрактора изображена на рис. 2. Если объектив телескопа построил изображение Солнца А'В' в своей фокальной плоскости S (плоскости S на рис. 1 и 2 -одна и та же плоскость), то окуляр с фокусным расстоянием f, расположенный на расстоянии от S, построит изображение Солнца А" В" на расстоянии Ъ от окуляра в плоскости S'. Отношение А"В"/А'В' определяет увеличение масштаба изображения, даваемое окуляром. Обозначим его через К. Оно выражается довольно простой формулой

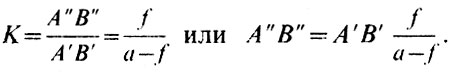
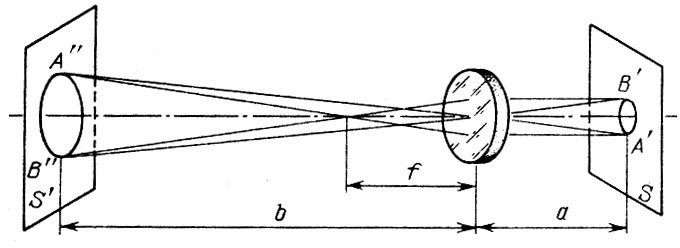
Рис. 2. Построение увеличенного изображения Солнца с помощью окуляра

Так как А'В'= 0,01 F для Солнца, то

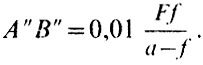
Из этой простой формулы следует, что если окуляр расположить на двойном фокусном расстоянии от плоскости S, т. е. а=2f, то изображение в плоскости S' получится того же размера, что и в плоскости S. При a=f на выходе будет система параллельных пучков. Удобно величину а выразить через увеличение масштаба

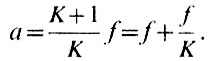
Посмотрим, на каком расстоянии мы можем получить изображение, если увеличение масштаба будет К. Из простого геометрического соотношения 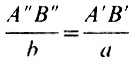и приведенных выше формул можно найти

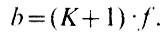
Применим полученные формулы к реальному расчету. Пусть мы имеем объектив, у которого F=1 м и окуляр с f=1 см, и хотим получить изображение Солнца диаметром 10 см. Мы уже знаем, что при F=1 м объектив построит изображение Солнца диаметром 1 см. Так как мы хотим иметь изображение 10 см, то нам нужно иметь увеличение K=10. Отсюда

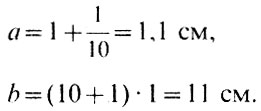
Таким образом, расстояние от фокальной плоскости объектива S до плоскости S' будет а+Ь=12,1. Весь телескоп будет иметь длину 112 см. Напомним, что для построения изображения Солнца размером 10 см при помощи одного объектива нам понадобилась бы труба длиной 10 метров. Как видно из формул для а и b, для того чтобы длина телескопа была меньше, надо выбирать окуляр с меньшим фокусным расстоянием. Казалось бы, что мы можем получить изображение Солнца любого размера при помощи окулярного увеличения и сравнительно небольшой длине трубы. Но какого качества и какой яркости будет это изображение?

Мы уже говорили, что нельзя разрешить на изображении Солнца точки, лежащие ближе, чем на расстоянии кружка рассеяния объектива, т. е. на расстоянии 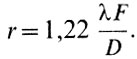Окулярное увеличение сделает этот кружок в К раз больше: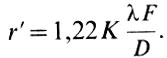

Для рассмотренного выше примера (D=100 мм, F=1000MM, F=10 мм, К=10)

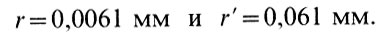
В этом случае мы еще не заметим глазом ухудшения изображения, но при K=100 и больше простым глазом уже будет видно, что изображение нерезкое. Кроме того, окуляр - такой же объектив, и он тоже имеет свой кружок рассеяния. Для него угловое разрешение 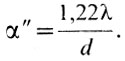В плоскости S' ему соответствует кружок радиусом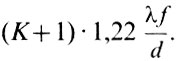Пока этот кружок будет меньше кружка рассеяния объектива, окуляр не будет портить изображение. В более удобной форме это условие

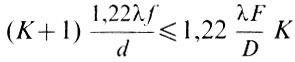
можно записать как

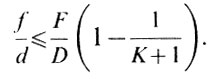
Для нашего случая F/D=10, K=10, f/d=2. Правая часть неравенства будет равна 9,1, а левая равна 2, т. е. неравенство выполняется и окуляр не портит изображения.

Обратимся к вопросу о яркости изображения. Посмотрим еще раз на рис. 2. Весь свет, прошедший через объектив телескопа, сходится в плоскости S, где создается изображение Солнца. После плоскости S лучи вновь расходятся. Если окуляр пропускает весь расходящийся пучок света, то после окулярного увеличения яркость единицы площади изображения Солнца в плоскости S' будет в К² раз меньше, чем в плоскости S. Если же окуляр слишком мал, то часть света от краевых пучков не попадет в него и пройдет мимо. Это приведет к тому, что части изображения Солнца, попадающие на края поля зрения, будут более темными. Этот эффект называется виньетированием изображения.

Существуют и другие методы получения большого изображения Солнца при умеренном размере трубы телескопа.

Так, в Службе Солнца нашей страны вот уже много лет для получения фотографий Солнца используется фотогелиограф АФР-3, в котором для уменьшения размера трубы применен телеобъектив. Оптическая схема этого телескопа показана на рис. 3. Изображение Солнца строится двумя линзами - выпуклой L₁ и вогнутой L₂, помещенными на расстоянии d друг от друга. Величина d должна быть больше алгебраической суммы фокусных расстояний обеих линз f₁+f₂, причем f₂<0. Такая система строит изображение в точке Ф, как если бы его давала одиночная линза L с фокусным расстоянием F, величина которого называется эквивалентным фокусным расстоянием. F определяется формулой

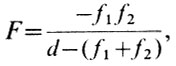
а общая длина трубы формулой

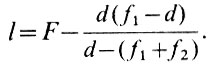
Обычно выбирают d чуть большим f₁+f₂. Тогда F большое, а l-невелико. Например, при f₁ = 80 см, f₂= -20 см, d=62 см будут F=800, a l=242 см. Таковы характеристики фотогелиографа АФР-3.

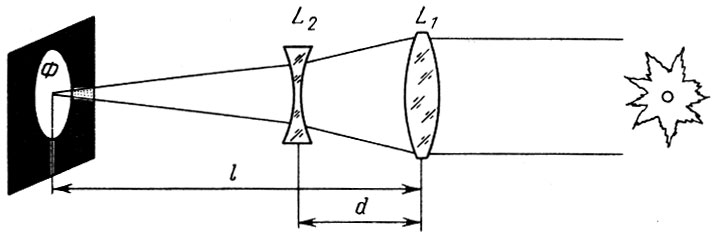
Рис. 3. Оптическая схема рефрактора с телеобъективом