Приборы для спектральных наблюдений

Если разложить солнечный свет в спектр, то открывается возможность получить из него значительно большую информацию.

Рассмотрим, с помощью каких приборов можно построить спектр Солнца.

Из школьного курса физики известно, что в пучке белого света лучи разных длин волн идут в одном направлении. Если на пути такого пучка поставить диспергирующий элемент, то лучи разных длин волн будут по разному отклоняться от первоначального направления. На этом принципе основаны все спектральные приборы. В качестве диспергирующих элементов чаще всего используют призмы и дифракционные решетки. На рис. 10 показано, как проходят лучи света через призму. Слева на призму падает пучок белого света. Верхнее на нашем чертеже ребро призмы называется преломляющим ребром. Луч света, падая на призму, попадает в среду с другим коэффициентом преломления и меняет свое направление. Так как коэффициент преломления п зависит от длины волны, то угол отклонения луча в призме будет разным для разных длин волн, Из призмы выйдет свет в виде бесконечной совокупности пучков света разных длин волн, т. е. разного цвета, близко отстоящих друг от друга, и вместо вошедшего в призму белого пучка мы получим перпендикулярную преломляющему ребру призмы окрашенную полоску, в которой цвета меняются от красного до фиолетового.

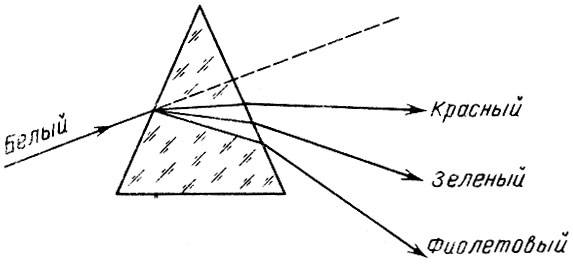
Рис. 10. Прохождение света через призму

Но одна призма не позволяет получить качественный спектр Солнца. Для этого нужен спектрограф, в котором кроме диспергирующего элемента есть еще щель, коллиматор и камера. Оптическая схема спектрографа с призмой показана на рис. 11. В левой части рисунка изображена входная щель спектрографа, перпендикулярная к плоскости чертежа. На телескопе она должна быть расположена в фокальной плоскости, и на ней строится изображение Солнца. Щель является источником света для спектрографа. От нее идет конус белого света, угол р которого определяется относительным отверстием телескопа D/F где D - диаметр объектива или главного зеркала телескопа, a F эквивалентное фокусное расстояние телескопа. Линза L, в фокусе которой находится щель, называется коллиматором. После коллиматора мы имеем параллельный пучок белого света, падающий на призму. Как мы говорили выше, из призмы выйдет система параллельных монохроматических (т. е. одной длины волны) пучков, в разной степени отклонившихся от первоначального направления белого пучка. Каждый из этих пучков падает на линзу L' - камеру, под своим углом и они будут собраны этой камерной линзой в ее фокальной плоскости в виде полоски спектра, перпендикулярной преломляющему ребру. Строго говоря, в фокальной плоскости камеры мы получили непрерывный ряд монохроматических изображений входной щели спектрографа. Красная часть спектра расположена ближе к направлению падающего пучка, а фиолетовая - дальше от него. Длина полученной полоски спектра зависит от преломляющего угла призмы, коэффициента преломления того материала, из которого сделана призма, и фокусного расстояния камерной линзы L'. На рис. 11 оно обозначено f'.

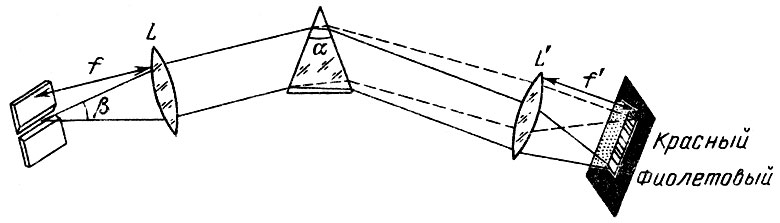
Рис. 11. Схема призменного спектрографа

Очень важной характеристикой, связанной с длиной спектра, является дисперсия спектрографа. Различают угловую и линейную дисперсию. Угловая дисперсия спектрографа - это производная угла отклонения луча в призме по длине волны 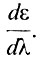Обычно за dλ принимают 1 Å =10^-8 см (ангстрем). Тогда угловая дисперсия - это изменение угла отклонения луча при изменении длины волны на 1Å(dε в радианах). Линейная дисперсия определяется в фокальной плоскости камеры как расстояние междуо линиями спектра, длины волн которых отличаются на 1Å,

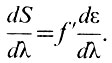
Формула для определения линейной дисперсии призменного спектрографа выглядит так:

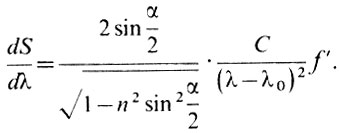
Здесь α - преломляющий угол призмы, n - коэффициент преломления стекла, из которого сделана призма, λ - длина волны, С и λ₀ - постоянные величины. Они зависят от сорта стекла.

Из этой формулы видно, что дисперсия призмы обратно пропорциональна длине волны. Отсюда следует, что красная часть спектра будет сжата, а синяя растянута.

Диспергирующим элементом может быть и дифракционная решетка. Как правило, она представляет собой толстую плоскопараллельную пластину с напыленным в вакууме слоем алюминия на одной поверхности. На этой поверхности специальным алмазным резцом нанесены параллельные бороздки - штрихи решетки. Количество штрихов на разных решетках бывает разное - от 50 до 1200 на миллиметр. Разложение в спектр падающего на такую решетку света происходит под действием двух физических законов: дифракции света на щели (штрихе в данном случае) и интерференции лучей, отраженных от каждого штриха. Мы не будем здесь останавливаться на теории дифракционной решетки, описанной во многих учебниках физики. Покажем на рис. 12, в каком направлении идут отраженные пучки разных цветов при падении на решетку белого света. Если на решетку под каким-то углом падает пучок белого света, то в направлении отраженного по обычному закону геометрической оптики пучка пойдет также белый свет, называемый нулевым порядком.

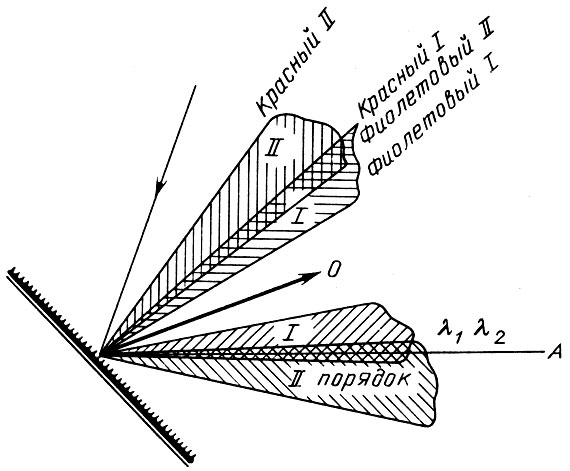
Рис. 12. Отражение света от дифракционной решетки

Этот свет отражается зеркальными промежутками между штрихами решетки. Свет, отраженный штрихами, даст спектры справа и слева от нулевого порядка. На рис. 12 показано по 2 таких спектра или порядка с каждой стороны. На самом деле их может быть гораздо больше. В отличие от спектра, получаемого с призмой, меньше всего отклоняются от направления белого пучка фиолетовая часть спектра, а больше - красная. Особенностью спектра является и то, что угол между лучами двух фиксированных длин волн растет с номером порядка. На рис. 12 видно, что угол между красным и фиолетовым светом во II порядке примерно в 2 раза больше, чем в I порядке. Еще одна существенная характеристика спектра - наложение порядков. В одном и том же направлении идут лучи, принадлежащие разным порядкам и имеющие разные длины волн. Закономерность этого наложения выражается следующей простой формулой:

kλ_k = const (константа, т. е. постоянная величина).

Здесь k - номер порядка, λ_к - длина волны излучения в k-м порядке. Поясним эту формулу на примере рис. 12. Пусть в направлении А в I порядке решетки (k=1) идет красный свет длиной волны λ₁ =6500 Å. Тогда по формуле находим значение константы const = 1*6500=6500. Подставим в исходную формулу k = 2, найдем, чему равна λ₂:

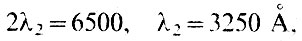
т. е. в направлении А идет свет из II порядка с длиной волны 3250 Å. Это ультрафиолетовый свет, к которому наш глаз нечувствителен, так что обнаружить его мы сможем только с помощью специальных приемников света.

Если мы хотим наблюдать во втором и более высоких порядках решетки, то там будет накладываться излучение разных длин волн из оптического диапазона, т. е. видимое человеческим глазом. Так, если во II порядке λ₂=6500 Å, к = 2, то в этом же направлении из III порядка идет излучение 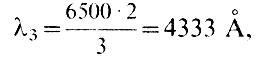что уже видно глазом. Чтобы разделить излучение разных порядков, обычно используют стеклянные цветные фильтры. В нашем случае, если мы хотим наблюдать красную область спектра во II порядке, надо перед щелью, а лучше после нее, поместить красный или оранжевый фильтр. Он не пропустит синий свет из II порядка (λ = 4333 Å). Если же надо наблюдать синюю область

в III порядке, следует синим фильтром "отрезать" красную часть спектра. О характеристиках стеклянных фильтров будет сказано ниже.

Спектрограф с дифракционной решеткой по своей схеме мало отличается от призменного спектрографа. Должны присутствовать те же основные элементы щель, коллиматор, камера. Но так как современные решетки в основном отражательные, то расположение этих элементов может быть другим. На рис. 13 приведена одна из возможных оптических схем спектрографа с решеткой. Здесь коллиматор и камера - вогнутые сферические зеркала. Фокусное расстояние коллиматора f а камеры f'. Другая схема (рис. 14) использует в качестве коллиматора и камеры один объектив.

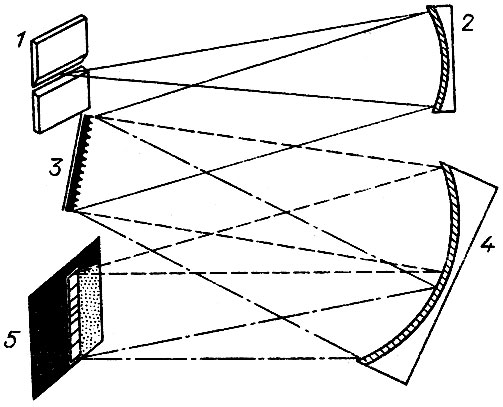
Рис. 13. Схема дифракционного спектрографа с зеркальными коллиматором и камерой: 1 - щель; 2 - коллиматор; 3 - дифракционная решетка; 4 - камера; 5 - фокальная плоскость, в которой строится спектр

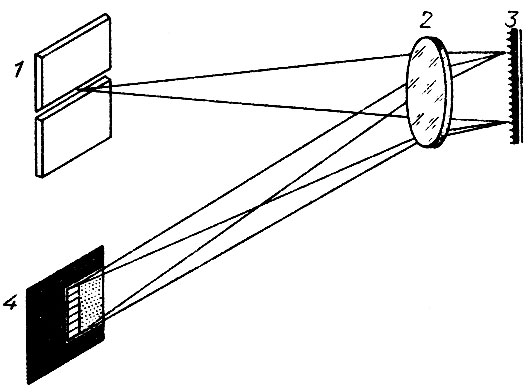
Рис. 14. Схема автоколлимационного спектрографа: 1 - щель; 2 - объектив, служащий коллиматором и камерой: 3 - дифракционная решетка; 4 - фокальная плоскость, в которой строится спектр

Важной характеристикой дифракционного спектрографа является его дисперсия. Для небольших углов падения света на решетку она выражается формулой

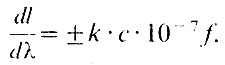
Здесь k - номер порядка спектра, с - число штрихов на 1 мм решетки, f - фокусное расстояние камеры в тех же единицах, что и dl линейное расстояние в фокальной плоскости камеры лучей, отличающихся по длине волны на dλ (в ангстремах). Обычно берут dλ=lÅ.

В качестве примера рассчитаем по этой формуле дисперсию в 1 порядке спектрографа с решеткой, имеющей 600 штрихов на мм. Фокусное расстояние камеры спектрографа 7 м = 7000 мм. Получим

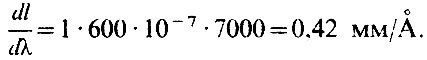
Часто пользуются обратной дисперсией, 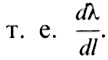В нашем случае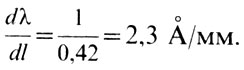

Если сравнить выражение для призменного и дифракционного спектрографов, то основная разница между ними в том, что в случае призменного спектрографа дисперсия зависит от длины волны λ, а в дифракционном не зависит. В нем дисперсия растет при переходе к более высоким порядкам (пропорционально номеру порядка к).

Остановимся на некоторых особенностях спектрографа, независимых от выбора диспергирующего элемента. Выбор той или иной схемы спектрографа, размеров его элементов зависит в немалой степени от характеристик телескопа, на выходе которого будет установлен спектрограф. Как говорят астрономы, спектрограф должен быть согласован с телескопом по светосиле. Поясним это на рис. 15. Слева условно изображен телескоп, диаметр объектива которого равен D, а фокусное расстояние F. В фокальной плоскости телескопа находится щель спектрографа, справа от которой расположен спектрограф (на рисунке показан только коллиматор). Свет, падающий на щель спектрографа, представляет собой конус с углом раствора D/F и вершиной О на щели. Естественно, что в спектрографе от щели свет будет распространяться в таком же конусе. Оптимальный размер коллиматора надо выбирать таким, чтобы весь пучок, прошедший через щель, прошел и через коллиматор (или отразился от него в случае сферического зеркала). Это условие равносильно равенству D/F=d/f, т. е. относительные отверстия (и светосилы) телескопа и коллиматора должны быть равны.

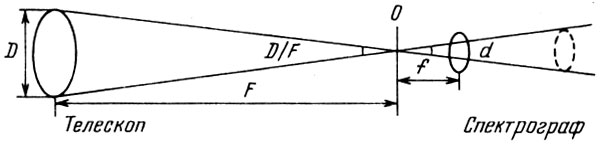
Рис. 15. Согласование телескопа и спектрографа по светосиле

Посмотрим теперь, каково может быть соотношение характеристик объективов (или зеркал) коллиматора и камеры. Так как, по сути дела, спектр есть последовательность монохроматических изображений входной щели, которые строят камера и коллиматор, то размер монохроматического изображения щели зависит от отношения фокусных расстояний коллиматора (f) и камеры (f'). Если ширина щели равна а, то ширина ее монохроматического изображения будет

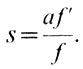
При большом s будет сильное переналожение соседних монохроматических изображений, т. е. уменьшится чистота спектра. Уменьшить s можно уменьшив f' или увеличив f. Выше мы приводили формулы дисперсии, из которых было видно, что с уменьшением фокусного расстояния камеры f' дисперсия будет уменьшаться. Поэтому для увеличения чистоты спектра лучше выбрать объектив (или зеркало) коллиматора с большим f. Что касается ширины щели а, то ее выбор не произволен. Из только что приведенной формулы видно, что чем шире щель, тем хуже чистота спектра. Но с уменьшением ширины щели в спектрограф проходит меньше света. Оптимальное значение ширины щели, называемое нормальной шириной щели, определяется формулой

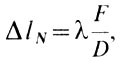
где λ - длина волны в тех же единицах, что и ширина щели Δl_N, F/D - наименьший из двух относительных фокусов- телескопа и коллиматора, если они не равны. На практике пользуются шириной щели, определяемой по этой формуле или несколько большей (до 2Δl_N).