
Глава I. Общие сведения о космических аппаратах и ракетах
В настоящее время созданы первые космические аппараты. Запуск их осуществляется с помощью многоступенчатых космических ракет, одним из видов которых являются ракеты-носители искусственных спутников.
В дальнейшем многообразие космических аппаратов будет непрерывно увеличиваться. Появятся космические аппараты, предназначенные для длительных полетов человека, искусственные спутники Луны и планет, постоянно существующие спутники-станции, космические корабли для полетов к другим планетам. Будут созданы новые типы космических ракет, в том числе ракеты с двигателями, работающими на ядерной энергии.
Сегодня невозможно предвосхитить все особенности устройства и конструкции космических аппаратов будущего, хотя в современной технической литературе встречается немало их описаний и проектов. Однако существует ряд вопросов и проблем, являющихся общими для всех космических аппаратов. К ним относится проблема придания космическим аппаратам необходимой скорости и точного выведения их на заданные орбиты, проблемы поддержания необходимого теплового режима и обеспечения энергией бортовой аппаратуры, измерения орбиты и передачи информации на расстояния, исчисляемые десятками и сотнями миллионов километров, вопросы герметизации, метеорной опасности, влияния космических излучений и ряд других.
В настоящей главе излагаются общие сведения о космических аппаратах и ракетах, законах их движения и особенностях устройства. Рассматриваются основные проблемы, связанные с длительным пребыванием космических аппаратов в межпланетном пространстве. Поясняется значение искусственных спутников для решения проблемы межпланетных полетов.
Законы движения космических аппаратов
Полет любого космического аппарата обычно разделяется на два основных этапа. На первом этапе космическая ракета, или ракета-носитель, сообщает ему необходимую скорость в заданном направлении. На втором этапе движение космического аппарата по определенной орбите происходит по инерции, при действии на него сил тяготения окружающих небесных тел. Соответственно траектория полета космического аппарата имеет два основных участка - участок выведения и орбитальный участок.
Для современных космических ракет, двигатели которых работают на химическом топливе, протяженность участка выведения обычно незначительна по сравнению с протяженностью орбитального участка. Поэтому при рассмотрении законов движения космических аппаратов мы будем интересоваться в основном вторым этапом полета - движением космических аппаратов после придания им необходимой скорости.
Исключением являются космические аппараты, разгон которых происходит с весьма малыми ускорениями, и, в частности, аппараты с так называемыми электрореактивными двигателями, проекты которых обсуждаются в технической литературе. У аппаратов этого типа двигатели работают на большей части траектории полета.
Прежде чем приступить к непосредственному рассмотрению законов движения космических аппаратов, остановимся вкратце на основных характеристиках нашей солнечной системы. Солнечная система (рис. 1) состоит из центрального небесного тела - Солнца, вокруг которого движутся по замкнутым орбитам девять больших планет и ряд малых небесных тел (малые планеты, астероиды, кометы, потоки метеорных тел).
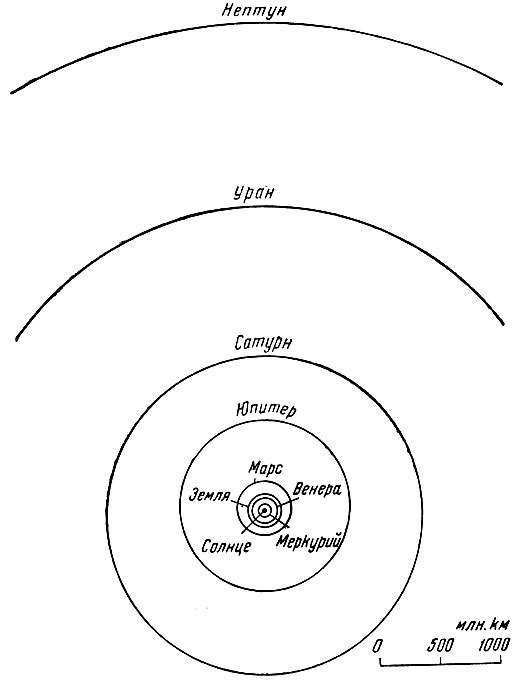
Рис. 1. Орбиты планет солнечной системы
Основные данные о планетах солнечной системы приведены в табл. 1. В табл. 2 содержатся данные, относящиеся к Луне.
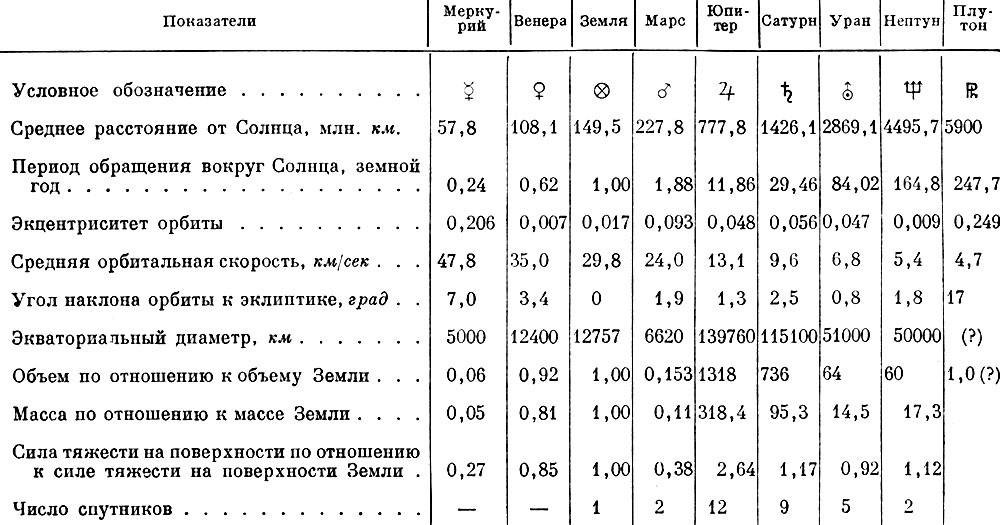
Таблица 1. Основные данные о планетах солнечной системы
| Расстояние от Земли, км | |
| в перигее | 356400 |
| в апогее | 406670 |
| среднее | 384400 |
| Период обращение вокруг Земли, сутки | 27,3 |
| Экцентриситет орбиты | 0,055 |
| Средняя орбитальная скорость, км/сек | 1,02 |
| Экваториальный диаметр, км | 3473 |
| Масса по отношению к массе Земли | 0,01228 |
| Сила тяжести на поверхности по отношению к силе тяжести на поверхности Земли | 0,166 |
Как видно из данных табл. 1, все планеты, кроме Плутона, имеют орбиты с небольшим эксцентриситетом - близкие к круговым, причем плоскости их орбит примерно совпадают. Движение планет происходит в одном направлении - против часовой стрелки, если наблюдать его со стороны Полярной звезды. У ряда планет имеются естественные спутники. К таким планетам относится и Земля, естественным спутником которой является Луна. Расстояния планет от Солнца в тысячи и десятки тысяч раз превышают их диаметры. Минимальные расстояния от Земли до ближайших планет Венеры и Марса составляют соответственно 39 и 56 млн.км.
Масса Солнца значительно больше массы планет. Она в тысячу раз превышает массу Юпитера и в 332 тыс. раз массу Земли.
На космический аппарат, как и на любое другое материальное тело, находящееся в солнечной системе, действуют силы тяготения Солнца, планет и других небесных тел. Величина силы притяжения космического аппарата к каждому из этих небесных тел зависит от расстояния до данного тела и его массы.
Как правило, одна из всех действующих на космический аппарат гравитационных сил является доминирующей. Если космический аппарат находится вблизи от одной из планет, то основной гравитационной силой, действующей на него, является сила притяжения к этой планете. Если же космический аппарат находится в межпланетном пространстве на достаточном удалении от отдельных планет, то основной действующей на него силой является сила притяжения к Солнцу.
В небесной механике существует понятие "сфера действия" небесного тела, определяемое следующим образом. Представим себе, что мы имеем два небесных тела - центральное тело большой массы М, например Солнце, и обращающееся вокруг него тело (меньшей массы m, например Землю. Предположим, что в поле тяготения этих тел находится третье тело, масса которого μ настолько мала, что практически не влияет на движение первых двух тел. Движение этого тела (например, космического аппарата) может рассматриваться как в системе координат, связанной с Солнцем,- гелиоцентрической системе, так и в системе координат, связанной с Землей, но не участвующей в ее суточном вращении,- геоцентрической системе*.
* (Обе эти системы совершают только поступательное движение и, следовательно, являются инерциальными.)
Сферой действия Земли по отношению к Солнцу называется область вокруг Земли, в которой отношение силы, с которой Солнце возмущает геоцентрическое движение тела μ, к силе притяжения этого тела Землей меньше, чем отношение силы, с которой Земля возмущает гелиоцентрическое движение тела μ к силе притяжения его Солнцем. т. е. в пределах сферы действия выполняется условие
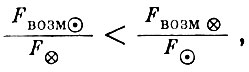
где 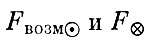 - соответственно возмущающая сила притяжения к Солнцу и сила притяжения к Земле при рассмотрении движения тела μ в геоцентрической системе;
- соответственно возмущающая сила притяжения к Солнцу и сила притяжения к Земле при рассмотрении движения тела μ в геоцентрической системе;
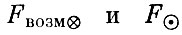
- соответственно возмущающая сила притяжения к Земле и сила притяжения к Солнцу при рассмотрении движения тела μ в гелиоцентрической системе.
Аналогично может быть определена сфера действия любого небесного тела по отношению к соответствующему центральному телу, например, сфера действия Луны по отношению к Земле. Радиус сферы действия малого тела по отношению к большому телу определяется формулой:
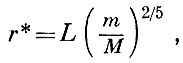 (1.2)
(1.2)где: М - масса большого тела;
m - масса малого тела;
L - расстояние между ними.
Значения радиусов сфер действия планет солнечной системы приведены в табл. 3. Радиус сферы действия Луны по отношению к Земле составляет около 66 тыс. км.
| Планета | Радиус, млн. км |
|---|---|
| Меркурий | 0,11 |
| Венера | 0,62 |
| Земля | 0,93 |
| Марс | 0,58 |
| Юпитер | 48,5 |
| Сатурн | 54,4 |
| Уран | 52,0 |
| Нептун | 87,5 |
В пределах сферы действия планеты характер движения космического аппарата определяется в основном полем ее тяготения. Поля тяготения других небесных тел, в том числе и Солнца, создают малые возмущения этого основного движения космического аппарата и в первом приближении могут не учитываться.
Соответственно вне сфер действия планет характер движения космического аппарата определяется в основном полем тяготения Солнца. Поля тяготения планет в этом случае создают малые возмущения гелиоцентрического движения космического аппарата. Таким образом, при изучении законов движения космических аппаратов следует в первую очередь рассмотреть задачу о движении их в поле тяготения одного небесного тела - в центральном поле тяготения.
Движение в центральном поле тяготения
В первом приближении можно считать, что Земля, как и другие небесные тела - Солнце и планеты, имеет форму шара и сферически симметричное распределение плотности. Поле тяготения при таком условии называется центральным, поскольку оно эквивалентно полю тяготения материальной точки, имеющей массу, равную массе данного небесного тела, и расположенной в его центре.
Представим себе, что в центральном поле тяготения находится космический аппарат, имеющий в начальный момент времени скорость V0 (рис. 2). Дальнейшее движение космического аппарата по инерции будет происходить в плоскости, проходящей через начальное его положение С, центр тяготения Ο и вектор скорости  .
.
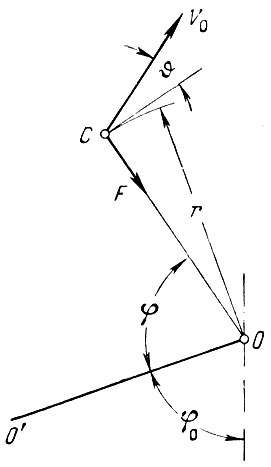
Рис. 2. Космический аппарат в центральном поле тяготения: V0-начальная скорость космического аппарата; F - сила притяжения его к центральному телу
Удобно изучать это движение в полярной системе координат, имеющей центр в точке О. Положение космического аппарата в этой координатной системе характеризуется величиной радиуса r и углом φ - по отношению к некоторому неизменному направлению, принятому за начало угловых координат 00'.
Единственной силой, действующей на космический аппарат, является сила притяжения его к центральному телу О, равная:
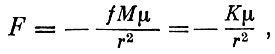 (1.3)
(1.3)где:
f - гравитационная постоянная;
М - масса центрального тела;
μ - масса космического аппарата;
К = fМ - постоянная поля тяготения.
Для Земли K⊗ = 3,986⋅105км3/сек2, для Луны 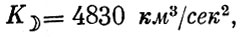 , для Солнца
, для Солнца 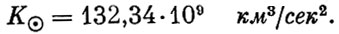 .
.
Определим потенциальную энергию космического аппарата, находящегося на расстоянии r от центра тяготения, предположив, что поверхность нулевого потенциала расположена в бесконечности.
Изменение потенциальной энергии при увеличении расстояния r на dr составляет:
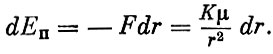
Интегрируя в пределах от ∞ до r, получим
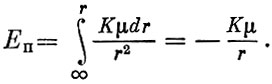 (1.4)
(1.4)Кинетическая энергия космического аппарата, движущегося со скоростью V, равна:
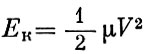
и, следовательно, его полная энергия составляет:
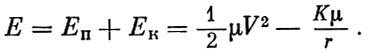 (1.5)
(1.5)В соответствии с законом сохранения энергии величина полной энергии в процессе движения остается постоянной.
Тогда, если в некоторый момент времени t = t0, радиус и скорость имели начальные значения r = r0 и V = V0, то
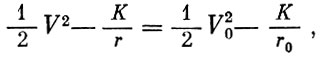 (1.6)
(1.6)
откуда, выразив величину скорости через производные полярных координат по времени 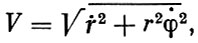 , получим:
, получим:
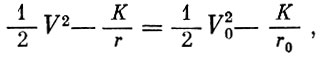 (1.7)
(1.7)Второе уравнение движения может быть получено из условия, что момент количества движения космического аппарата относительно центрального тела в процессе движения остается величиной постоянной:
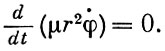 (1.8)
(1.8)
Здесь 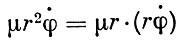 - момент количества движения.
- момент количества движения.
Интегрирование этого уравнения непосредственно приводит ко второму закону Кеплера:
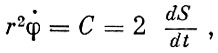 (1.9)
(1.9)где С - так называемая постоянная закона площадей;
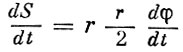 - секториальная скорость - площадь,
- секториальная скорость - площадь,
описываемая радиусом-вектором r в плоскости орбиты в единицу времени. Принимая во внимание начальные условия: r = r0, V = V0,  =
=  0 при t = t0, можем представить это уравнение в виде:
0 при t = t0, можем представить это уравнение в виде:
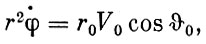 (1.10)
(1.10)
где  - угол наклона вектора скорости к плоскости, перпендикулярной радиусу-вектору r (т. е. к горизонту). Уравнения (1.7) и (1.10) являются уравнениями движения космического аппарата как материальной точки в центральном поле тяготения. Решая их совместно и исключив время t, получим уравнение орбиты космического аппарата (см. прилож. 1):
- угол наклона вектора скорости к плоскости, перпендикулярной радиусу-вектору r (т. е. к горизонту). Уравнения (1.7) и (1.10) являются уравнениями движения космического аппарата как материальной точки в центральном поле тяготения. Решая их совместно и исключив время t, получим уравнение орбиты космического аппарата (см. прилож. 1):
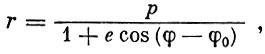 (1.11)
(1.11)где
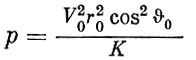 (1.12)
(1.12)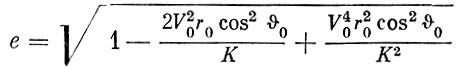 (1.13)
(1.13)φ0 - некоторое значение угла φ, включающее в себя постоянную интегрирования.
Из формулы (1.13) следует, что орбита космического аппарата, движущегося в центральном поле тяготения, в полярной системе координат представляет кривую второго порядка, один из фокусов которой расположен в начале координат.
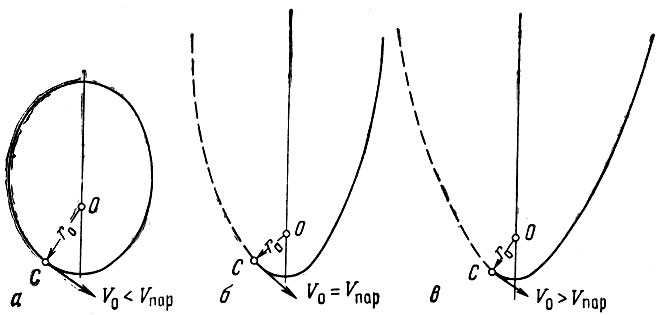
Рис. 3. Типы орбит: а - эллиптическая орбита; б - параболическая орбита; в - гиперболическая орбита
Коэффициент р - параметр, е - эксцентриситет кривой.
При е < 1 радиус-вектор r остается конечным для всех значений φ, и орбита является замкнутой кривой - эллипсом (рис. 3,а). В частном случае, при е = 0, этот эллипс превращается в окружность. При е = 1 радиус-вектор г становится бесконечным при φ - φ0 = π. Орбита в этом случае является незамкнутой кривой-параболой (рис. 3,6). Наконец, при е > 1 радиус-вектор r становится бесконечным при φ - φ0 = ± arc cos (-1/е). В этом случае орбита является гиперболой (рис. 3, в).
Характер орбиты, как это видно из формулы (1.13), зависит от соотношения начальной скорости V0 и величины 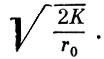 . Эта величина носит название параболической или второй космической скорости:
. Эта величина носит название параболической или второй космической скорости:
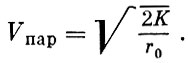
(1.14)
Если начальная скорость космического аппарата V0 < V пар, то движение его происходит по эллиптической орбите, если V0 = Vпар - по параболической, а если V0 > Vпар - по гиперболической орбите. Значение параболической скорости зависит исключительно от массы центрального тела М (так как К = fМ) и от расстояния до центра тяготения r0.
Для Земли на уровне ее поверхности параболическая скорость равна Vпар = 11,19 км/сек. С увеличением высоты значение параболической скорости уменьшается (табл. 4). Значения параболической скорости для других планет солнечной системы приведены в табл. 5.
| Высота, км | Параболическая скорость, км/сек |
|---|---|
| 0 | 11,19 |
| 500 | 10,77 |
| 1000 | 10,40 |
| 2000 | 9,76 |
| 5000 | 8,37 |
| 10000 | 6,98 |
| Планета | Параболическая скорость, км/сек |
|---|---|
| Меркурий | 4,15 |
| Венера | 10,25 |
| Земля | 11,19 |
| Луна | 2,36 |
| Марс | 5,09 |
| Юпитер | 60,2 |
| Сатурн | 36,2 |
| Уран | 21,4 |
| Нептун | 23,4 |
При скорости, равной параболической, космический аппарат приобретает кинетическую энергию, достаточную для удаления его в бесконечность, по отношению к центральному телу. Рассмотрим теперь, при каких условиях возможно движение космического аппарата по круговой орбите.
При е = 0 уравнение (1.11) примет вид: r = р = const. Одновременно из формулы (1.13) получим:
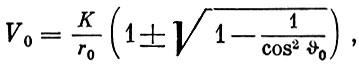 (1.15)
(1.15)
откуда следует, что скорость V0 при е = 0 может иметь вещественное значение только при  0 = 0. Это означает, что движение космического аппарата по круговой орбите возможно лишь при условии, что направление вектора начальной скорости перпендикулярно радиусу-вектору r, т. е. горизонтально.
0 = 0. Это означает, что движение космического аппарата по круговой орбите возможно лишь при условии, что направление вектора начальной скорости перпендикулярно радиусу-вектору r, т. е. горизонтально.
Скорость движения космического аппарата в этом случае:
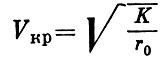 (1.16)
(1.16)носит название круговой или первой космической скорости. Значения параболической и круговой скоростей связаны между собой однозначно:
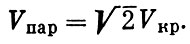 (1.17)
(1.17)Скорость космического аппарата в любой точке его орбиты можно определить, исходя из условий сохранения его полной энергии (1.6):
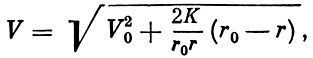 (1.18)
(1.18)где r - радиус-вектор, соответствующий данной точке.
Рассмотрим более подробно эллиптические орбиты. Схема орбиты такого типа дана на рис. 4.
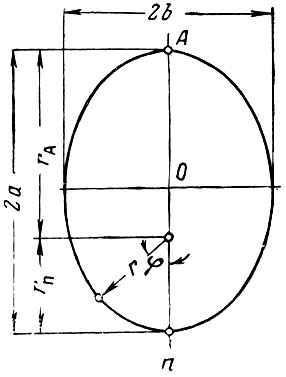
Рис. 4. Эллиптическая орбита; О - центр тяготения; r и φ- координаты космического аппарата в полярной системе; П - точка перигея; А - точка апогея; rП - перигейное расстояние; rA- апогейное расстояние; а - большая полуось орбиты
Для орбиты космического аппарата, движущегося вокруг Земли, точка A, соответствующая минимальному значению r, носит название перигея, а точка А, соответствующая максимальному значению r, - апогея. Для орбиты космического аппарата, или какого-либо небедного тела (планеты), движущегося вокруг Солнца, соответствующие точки носят название перигелия и афелия.
Как видно из формулы (1.11), минимальное и максимальное значения г составляют:
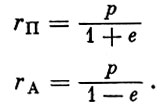 (1.19)
(1.19)При этом точки П и А диаметрально противоположны, поскольку значения угла φ для этих точек различаются между собой на φ. Линия AП, называемая линией апсид, является большой осью эллипса.
Сумма rП и rА равна большой оси эллипса. Следовательно, величина большой полуоси эллиптической орбиты
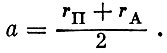
(1.20)
Учитывая выражения (1.19), получим
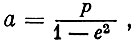 (1.21)
(1.21)или р = а(1 - е2).
Откуда, принимая во внимание выражения (1.19), следует:
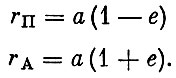 (1.22)
(1.22)Исключая из формулы (1.22) а, можно получить также зависимость е от rП и rA:
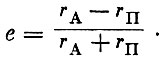 (1.23)
(1.23)Выразим теперь основные параметры эллиптической орбиты в зависимости от скорости в перигее VП и перигейного расстояния rП.
Из выражений (1.12) и (1.13) при  0 = 0 имеем:
0 = 0 имеем:
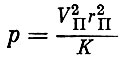 (1.24)
(1.24)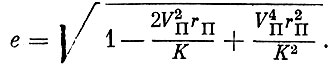 (1.25)
(1.25)Тогда большая полуось эллиптической орбиты будет равна:
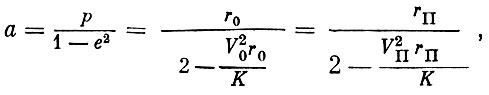 (1.26)
(1.26)и апогейное расстояние
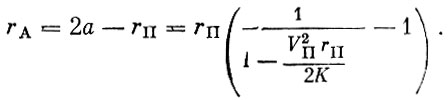 (1.27)
(1.27)
Как видно из формулы (1.26), большая полуось орбиты определяется величиной V0 и радиуса-вектора r0 в конце участка выведения и не зависит от направления скорости V0 (т. е. от угла  0).
0).
Из формулы (1.27) можно получить выражение для скорости в перигее:
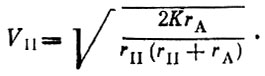 (1.28)
(1.28)Скорость в апогее связана со скоростью в перигее соотношением, непосредственно вытекающим из второго закона Кеплера:
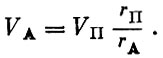 (1.29)
(1.29)Следовательно, скорость в апогее
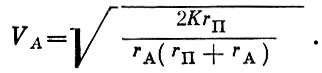 (1.30)
(1.30)Период обращения по эллиптической орбите выражается формулой (см. прилож. 1):
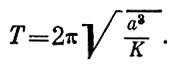 (1.31)
(1.31)Из формулы следует, что период обращения зависит только от величины большой полуоси орбиты и массы центрального тела.
Движение космического аппарата, как и любого другого материального тела в центральном поле тяготения, называется кеплеровым движением. Приведенные выше зависимости позволяют определить основные характеристики такого движения.
Особенности движения спутников
При движении спутника по эллиптической орбите (рис.5) высота его над поверхностью Земли h изменяется. В частном случае, когда высоты апогея и перигея одинаковы, орбита является круговой, и высота спутника над поверхностью Земли все время остается постоянной (рис. 6). Степень вытянутости орбиты может быть охарактеризована ее эксцентриситетом Эксцентриситет, большая полуось орбиты, перигейное и апогейное расстояния связаны между собой соотношениями (1.20) и (1.23).
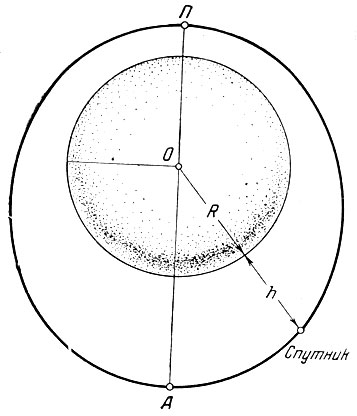
Рис. 5. Орбита спутника: R - радиус Земли; h - высота спутника над поверхностью Земли; П - точка перигея; А - точка апогея; О - центр Земли
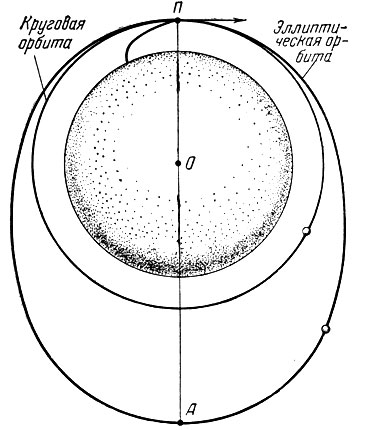
Рис. 6. Эллипитическая и круговая орбиты спутника
Из этих соотношений следует, что большая полуось равна среднему расстоянию спутника от центра Земли:
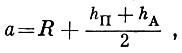 (1.32)
(1.32)а эксцентриситет орбиты зависит от разности высот апогея и перигея:
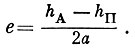 (1.33)
(1.33)Поскольку большая полуось эллиптической орбиты равна среднему расстоянию спутника от центра Земли, период обращения спутника вокруг Земли зависит, в соответствии с формулой (1.31), от средней высоты его полета (табл. 6).
| Средняя высота полета, км | Период обращения, часы |
|---|---|
| 0 | 1,41 |
| 250 | 1,49 |
| 500 | 1,58 |
| 750 | 1,66 |
| 1000 | 1,75 |
| 1500 | 1,93 |
| 1690 | 2,00 |
| 2000 | 2,12 |
| 5000 | 3,35 |
| 10000 | 5,78 |
| 35800 | 23,935 |
Из данных табл. 6 видно, что при средней высоте полета в несколько сот километров период обращения спутника составляет примерно 1,5 часа, при высоте полета 1690 км он равен 2 часам, а при высоте полета 35 800 км период обращения равен звездным суткам (периоду обращения Земли вокруг своей оси).
Спутник, запущенный в восточном направлении и выведенный на круговую орбиту, лежащую в плоскости экватора на высоте 35 800 км, находился бы все время над одной и той же точкой земной поверхности.
При движении спутника по круговой орбите скорость его постоянна и равна первой космической скорости на высоте полета спутника.
Значения круговой скорости для различных высот даны в табл. 7.
| Высота, км | Круговая скорость, м/сек |
|---|---|
| 0 | 7909 |
| 250 | 7759 |
| 500 | 7617 |
| 750 | 7482 |
| 1000 | 7354 |
| 1500 | 7116 |
| 1690 | 7032 |
| 2000 | 6901 |
| 5000 | 5921 |
| 10000 | 4935 |
| 35800 | 3072 |
Круговая скорость у поверхности Земли составляет около 7900 м/сек. С увеличением высоты круговая скорость уменьшается. Для высоты 35 800 км (орбита с периодом &&& 24 часа) она составляет примерно 3070 м/сек.
При движении спутника по эллиптической орбите скорость его периодически изменяется, достигая максимального значения в перигее и минимального - в апогее орбиты. Скорость спутника в перигее превышает круговую скорость на высоте перигея, а скорость в апогее меньше, чем круговая скорость на высоте апогея.
В табл. 8 приведены значения скорости движения спутника в перигее и апогее для орбит с различными высотами перигея и апогея

Таблица 8. Значения скорости спутника в перигее и апогее орбиты
Ориентация орбиты в пространстве и ее положение по отношению к земной системе координат обычно определяются величиной наклонения орбиты и величиной прямого восхождения ее восходящего узла. Наклонение орбиты i - это угол между плоскостью орбиты и плоскостью земного экватора. Восходящим узлом орбиты называется точка орбиты, в которой спутник пересекает плоскость земного экватора, переходя из южного полушария в северное. Соответственно, противоположная точка на орбите называется нисходящим узлом, а линия, соединяющая эти точки, - линией узлов. Прямым восхождением восходящего узла Ω называется угол между линией узлов и направлением на точку весеннего равноденствия.
Наряду с указанием ориентации плоскости орбиты в пространстве, необходимо указать ориентацию самой орбиты в этой плоскости и положение спутника на орбите в данный момент времени. Для этой цели обычно используются угловое расстояние перигея от восходящего узла ω (угол между линией узлов и линией апсид) и время прохождения спутника через восходящий узел орбиты t0.
Таким образом, движение спутника по орбите может быть охарактеризовано шестью следующими ее элементами: наклонением орбиты i, прямым восхождением восходящего узла Ω, большой полуосью орбиты а, ее эксцентриситетом е, угловым расстоянием перигея ω и временем прохождения спутника через восходящий узел t0 (рис. 7).
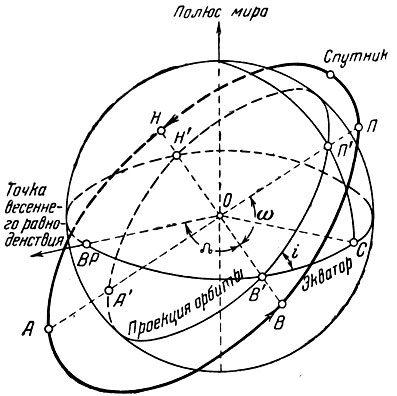
Рис. 7. Элементы орбиты спутника 1 - наклонение орбиты; Ω - прямое восхождение восходящего узла; ω - угловое расстояние перигея от восходящего узла; П - перигей орбиты; П' - проекция перигея на поверхность Земли; А - апогей орбиты; А' - проекция апогея на поверхность Земли; В - восходящий узел орбиты; В' - проекция восходящего узла на поверхность Земли; Н- нисходящий узел орбиты; Н' - проекция нисходящего узла на поверхность Земли; ВР - положение точки весеннего равноденствия на экваторе
При движении спутника в центральном поле тяготения и отсутствии сопротивления атмосферы первые пять элементов орбиты остаются постоянными, а периодическое движение спутника по орбите может продолжаться неопределенно большой промежуток времени.
Однако в действительности на движение спутника Земли оказывает влияние ряд дополнительных факторов. К ним относятся: сопротивление атмосферы, отличие поля тяготения Земли от центрального, поля тяготения Солнца и Луны.
Влияние этих факторов за ограниченные промежутки времени сравнительно невелико и в связи с этим может рассматриваться как возмущения основного, кеплерового, движения спутника, описанного выше.
Истинное движение спутника может быть представлено как движение его по кеплеровой орбите, основные элементы которой непрерывно изменяются, являясь функциями времени. Текущие значения элементов орбиты в этом случае называются оскулирующими элементами.
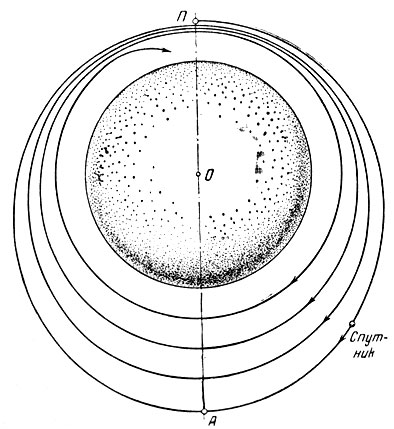
Рис. 8. Изменение формы орбиты спутника со временем вследствие сопротивления атмосферы: П - начальное положение перигея орбиты; А - начальное положение апогея орбиты
Для спутников, движущихся в пределах верхних слоев атмосферы, сопротивление ее постепенно изменяет скорость движения спутника и вызывает непрерывные (вековые) изменения формы его орбиты. Наиболее существенно спутник тормозится в периоды прохождения области перигея. В результате торможения спутника уменьшается его кинетическая энергия и сокращается апогейное и перигейное расстояния. При этом уменьшение апогейного расстояния и высоты апогея происходит значительно быстрее, чем уменьшение перигейного расстояния и высоты перигея. Эксцентриситет орбиты непрерывно уменьшается и сама орбита стремится к круговой (рис. 8). Торможение спутника по мере сокращения его орбиты прогрессивно возрастает. В конечном счете спутник, постепенно снижаясь, входит в плотные слои атмосферы, где разрушается и сгорает вследствие сильного нагревания. После снижения высоты орбиты до 150 км спутник совершает всего лишь 1-2 оборота. Продолжительность движения спутника от момента выведения его на орбиту до полного торможения в плотных слоях атмосферы называется временем его существования.
Степень торможения спутника при прочих равных условиях зависит от его аэродинамических характеристик - коэффициента сопротивления и отношения веса к площади миделя (поперечного сечения), так называемой поперечной нагрузки.
Оказывается возможным установить универсальное соотношение между скоростью изменения высоты апогея и перигея орбиты. Это соотношение определяется только параметрами орбиты и распределением плотности атмосферы по высоте и не зависит от весовых и аэродинамических характеристик спутника. Указанный результат позволяет составить простые таблицы для определения времени существования спутника на орбите.
Время существования для спутника весом 100 кг и диаметром 1 м в зависимости от начальных значений высоты перигея и апогея эллиптической орбиты дано в табл. 9. В табл. 10 приведены данные о времени существования подобного спутника при круговых орбитах.
Данные этих таблиц основаны па результатах теоретического исследования*.
* (См. Успехи физических наук, 1957, т. LXIII, вып. 1а, стр. 33.)
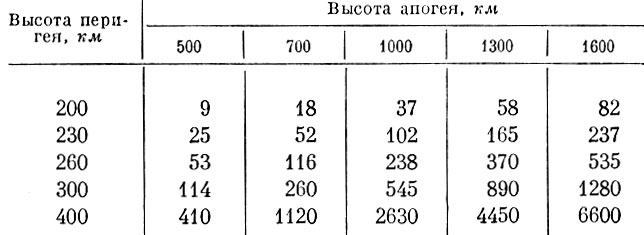
Таблица 9. Время существования спутника (в сутках) на эллиптических орбитах
Изданных таблиц видно, что для рассматриваемого спутника время существования при начальной высоте перигея 230 км и высоте апогея орбиты 700 км составляет около 50 суток. Увеличение высоты апогея на 300 км (до 1000 км) приводит к возрастанию времени существования в два раза. Примерно такое же возрастание времени существования получается при увеличении высоты перигея всего на 25 км (до 225 км). Для круговых орбит увеличение высоты с 300 до 400 км увеличивает время существования примерно в восемь раз, а до 500 км - еще в шесть раз.
| Высота круговой орбиты, км | Время существования, сутки |
|---|---|
| 200 | 0,4 |
| 250 | 4 |
| 300 | 20 |
| 350 | 65 |
| 400 | 160 |
| 500 | 1010 |
Для спутников, обладающих различными значениями коэффициентов сопротивления и нагрузки на мидель, время существования, при прочих равных условиях, прямо пропорционально значению поперечной нагрузки и обратно пропорционально коэффициенту сопротивления. Так, для спутника, имеющего диаметр 2 м при весе 1000 кг, время существования увеличится в 2,5 раза по сравнению с данными, приведенными в табл. 9 и 10.
Из сказанного становится очевидным, что зависимость времени существования спутника от высоты орбиты - очень сильная. При высоте полета спутника порядка нескольких тысяч километров движение его происходит за пределами верхних слоев атмосферы. Такой спутник практически может считаться постоянным спутником Земли.
Сжатие Земли у полюсов и связанное с ним отклонение поля тяготения от центрального также вызывают возмущения орбиты, которые можно разделить на периодические и вековые. Периодические возмущения орбиты за счет не центральности поля сравнительно невелики и сводятся к отклонениям действительных координат спутника от координат, соответствующих движению по эллипсу - около десятка километров. Вековые возмущения, действуя все время в одну и ту же сторону, приводят с течением времени к существенным изменениям элементов орбиты.
Основным вековым возмущением орбиты спутника за счет нецентральности поля земного тяготения является прецессия орбиты - равномерное вращение ее плоскости в абсолютном пространстве относительно земной оси. При этом наклонение орбиты остается примерно неизменным.
Скорость прецессии (величина ее за один оборот спутника по орбите) определяется формулой:
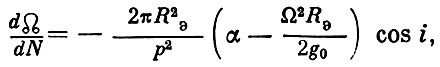 (1.34)
(1.34)где:
RЭ - экваториальный радиус Земли,
α - сжатие Земли;
Ω - угловая скорость суточного вращения Земли,
g0 - ускорение силы земного тяготения на экваторе;
p - параметр эллиптической орбиты;
i - наклонение орбиты;
N - порядковый номер оборота спутника вокруг Земли.
Как следует из формулы, скорость прецессии существенно зависит от наклонения орбиты.
При наклонении, равном 65°, и высотах, соответствующих высотам орбиты первого советского спутника прецессия орбиты составляет примерно 1/4° за один оборот спутника (рис. 9). При наклонении орбиты, равном 90° (полярная орбита), скорость прецессии равна нулю.
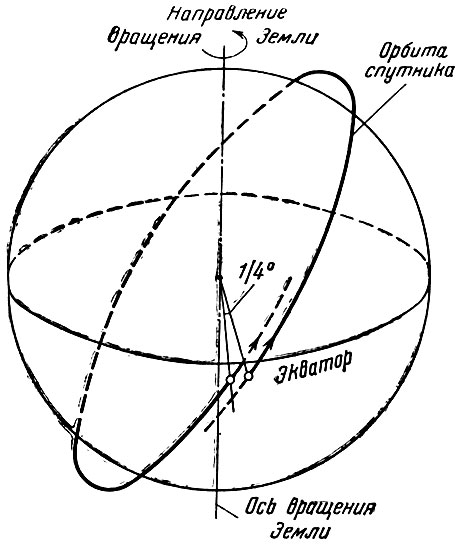
Рис. 9. Прецессия орбиты в пространстве
Другим вековым возмущением за счет нецентральности поля тяготения является поворот большой оси эллипса в плоскости орбиты - изменение углового расстояния перигея от восходящего узла ω. При этом происходит смещение области перигея (и соответственно апогея) от одних географических широт к другим.
Скорость поворота большой оси эллиптической орбиты характеризуется изменением углового расстояния перигея от восходящего узла за один оборот спутника по орбите:
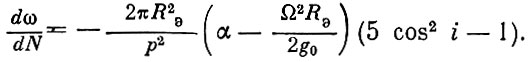 (1.35)
(1.35)
Как видно из формул, при 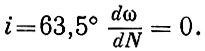 .
.
В соответствии с формулами (1.34) и (1.35) скорость прецессии орбиты и скорость ухода перигея обратно пропорциональны квадрату параметра орбиты р. Следовательно, для спутников, движущихся на значительных расстояниях от Земли (порядка нескольких десятков тысяч километров), прецессия орбиты и уход перигея за счет нецентральности поля тяготения Земли будут незначительными.
Таким образом, сжатие Земли не вызывает вековых изменений формы орбиты. Вековые возмущения орбиты за счет сжатия Земли проявляются в изменении ориентации ее в абсолютном пространстве. Сопротивление атмосферы, наоборот, практически не влияет на ориентацию орбиты, но вызывает значительные вековые изменения ее формы.
Влияние полей тяготения Солнца и Луны на движение близкого к Земле спутника весьма мало. Однако с увеличением высоты орбиты оно существенно возрастает.
Для орбиты с высотой апогея порядка многих десятков или нескольких сотен тысяч километров возмущающие влияния Солнца и Луны могут вызвать заметные изменения параметров и прежде всего - высоты перигея. В зависимости от расположения орбиты по отношению к Солнцу высота перигея может либо уменьшаться, либо увеличиваться. Уменьшение высоты перигея приведет в конечном счете к тому, что спутник войдет в плотные слои атмосферы, где и разрушится. В результате этого время существования искусственного спутника Земли, движущегося по орбите с высоким апогеем, может оказаться весьма ограниченным. Так, советская автоматическая межпланетная станция после сближения с Луной двигалась по орбите с высотой апогея примерно 480 тыс. км при высоте перигея около 40 тыс. км. На таких высотах сопротивление атмосферы отсутствует. Тем не менее возмущающее влияние притяжения Солнца вызвало столь быстрое сокращение перигейного расстояния, что продолжительность движения межпланетной станции по орбите, до вхождения ее в плотные слои атмосферы, составила около полугода. В качестве другого примера приведем результаты расчета движения спутника Земли по орбите с высотой апогея около 260 тыс. км (рис. 10). Уже на первых пяти оборотах спутника по орбите заметно ее изменение под действием возмущения полем притяжения Луны.
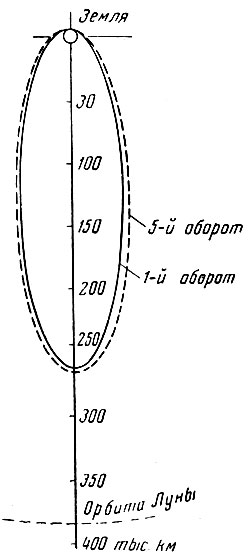
Рис. 10. Изменения орбиты спутника под действием поля тяготения Луны
Движение спутника по отношению к Земле является результатом сложения его движения по орбите, суточного вращения Земли и прецессии плоскости орбиты.
Рассмотрим движение спутника, начиная с некоторой точки орбиты. За время одного оборота спутника по орбите, т. е. к моменту прихода его на исходную географическую широту, Земля повернется на некоторый угол, зависящий от периода обращения спутника. Одновременно на небольшой угол повернется и сама плоскость орбиты вследствие ее прецессии. В результате, в начале следующего витка спутник окажется над точкой земной поверхности, находящейся к западу от исходной точки.
Проекция движения спутника на земную поверхность называется трассой. Легко показать, что трасса спутника на земной поверхности проходит в пределах двух параллелей, симметричных относительно экватора. Эти параллели соответствуют значениям северной и южной широт, по величине равным наклонению орбиты. Коснувшись одной из этих параллелей, трасса уходит к экватору, пересекает его, затем подходит к другой параллели, касается ее, снова пересекает экватор и опять подходит к первой параллели.
Далее ход трассы периодически повторяется, причем каждый из ее участков, соответствующих очередному обороту спутника по орбите, смещается по отношению к предыдущему по долготе. Угол пересечения трассы с экватором несколько отличается от угла наклонения плоскости орбиты, что объясняется вращением Земли.
Трасса спутника за сутки, при периоде его обращения по орбите, равном примерно 1,6 часа, показана на рис. 11.
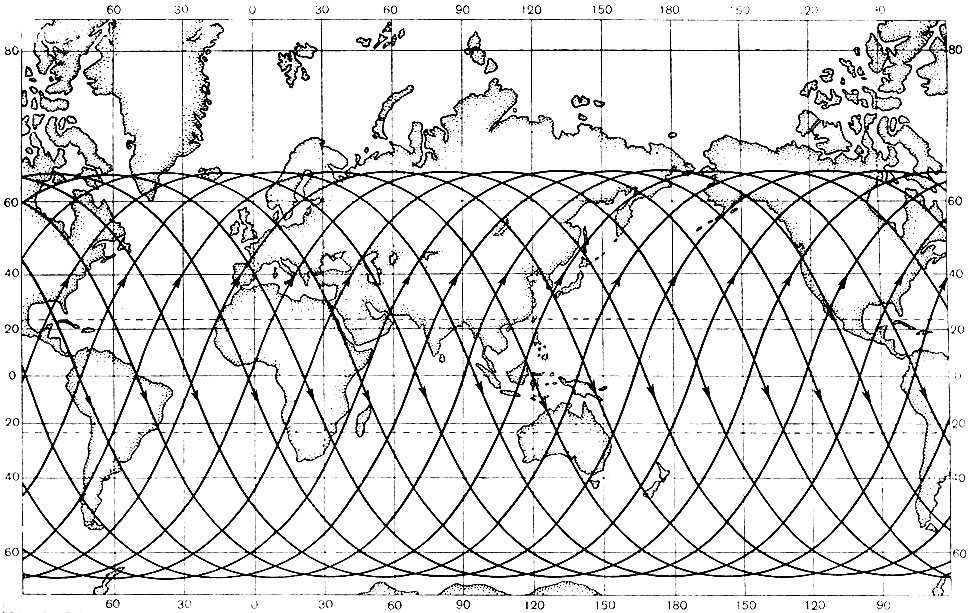
Рис. 11. Трасса спутника за сутки
Область географических широт, в пределах которых проходит трасса спутника, как указывалось выше, зависит от наклонения орбиты. Предельными случаями по величине наклонения плоскости орбиты являются: полярная орбита, проходящая через Северный и Южный полюсы, и экваториальная орбита, лежащая в плоскости экватора (рис. 12).
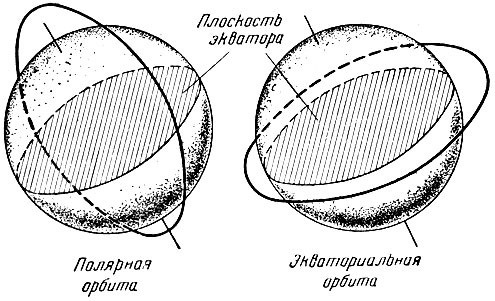
Рис. 12. Полярная и экваториальная орбиты
Наряду с искусственными спутниками Земли, могут быть созданы искусственные спутники Луны и других планет. Характеристики движения таких спутников на круговых орбитах - период обращения и круговая скорость - в зависимости от высоты орбиты над поверхностью планеты приведены в табл. 11.
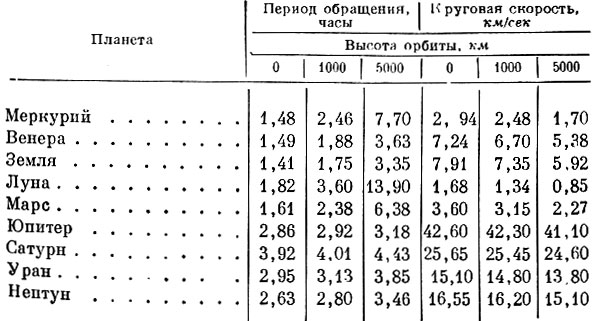
Таблица 11. Характеристики движения искусственных спутников планет и Луны
При малых высотах орбит период обращения искусственных спутников других планет и Луны больше, чем период обращения искусственных спутников Земли. Объясняется это тем, что плотности других планет меньше плотности Земли. Период же обращения спутника, движущегося у поверхности небесного тела, зависит исключительно от средней плотности этого тела-он обратно пропорционален корню квадратному из плотности.
Знание законов движения искусственных спутников позволяет решить задачу об изучении плотности верхних слоев атмосферы, а также гравитационного поля Земли - на основе наблюдений за изменением орбит спутников. Поскольку между изменением орбиты спутника и плотностью атмосферы существует прямая связь, анализ движения искусственных спутников может дать чрезвычайно ценные сведения о действительных значениях плотности атмосферы на больших высотах. По имеющимся в настоящее время данным, распределение плотности атмосферы на больших высотах сильно зависит от географической широты, времени суток и времени года. Поэтому для изучения распределения плотности атмосферы чрезвычайно важным является совместная обработка результатов наблюдений за спутниками, запускаемыми в различные времена года и имеющими различные наклонения плоскости орбиты и высоты перигея.
Кроме данных по плотности атмосферы, из анализа движения искусственных спутников можно получить уточненные значения напряженности поля земного тяготения, а также степень сжатия Земли и величину ее большой полуоси. При достаточно высокой точности измерения координат спутника и определенном размещении измерительных пунктов можно получить также более детальные сведения о поле земного тяготения и, в частности, определить интенсивности аномалий силы тяготения в различных точках земной поверхности.
Помимо изучения движения центра тяжести искусственного спутника, большой интерес представляет изучение его движения относительно центра тяжести.
Неориентированный спутник, обладающий продольной осью симметрии, под действием возмущений, имеющих место при его отделении от ракеты-носителя, начинает совершать прецессионное движение, вращаясь относительно своей продольной оси, которая в свою очередь вращается вокруг оси прецессии, составляя с ней некоторый угол.
При отсутствии воздействия атмосферы и других возмущающих факторов на орбите положение оси прецессии в пространстве относительно звезд остается неизменным.
Однако для искусственных спутников Земли положение оси прецессии в пространстве в большинстве случаев медленно изменяется под влиянием аэродинамических сил и гравитационного поля Земли. Кроме того, под воздействием электромагнитных сил постепенно уменьшается скорость вращения спутника. Проводя измерение положения спутника в отдельные моменты времени и обрабатывая результаты этих измерений с учетом уравнений движения спутника, можно получить полную картину его движения относительно центра тяжести.
В заключение следует отметить, что знание текущей ориентации спутника чрезвычайно важно с точки зрения постановки многих научных экспериментов. При анализе движения спутника по орбите знание его ориентации в ряде случаев также необходимо, поскольку при удлиненной форме спутника коэффициент аэродинамического сопротивления существенно зависит от его ориентации по отношению к вектору скорости.
Особенности движения космическим аппаратов в солнечной системе. Полеты к Луне, Марсу и Венере. Искусственные планеты
Как указано выше, при анализе движения космического аппарата оказывается возможным, в первом приближении, учитывать поле тяготения лишь того небесного тела, в сфере действия которого космический аппарат находится. При этом условии движение космического аппарата в пределах сферы действия каждого из небесных тел (рассматриваемое в системе координат, связанной с этим телом) происходит по одному из конических сечений - эллипсу, параболе или гиперболе и является кеплеровым движением.
При достижении космическим аппаратом границы сферы действия параметры его движения должны быть пересчитаны в новую систему координат, связанную с тем небесным телом, в сфере действия которого будет происходить дальнейшее движение космического аппарата.
Указанная приближенная методика изучения движения космических аппаратов по отдельным характерным участкам, несмотря на ее простоту, позволяет тем не менее во многих случаях достаточно точно установить важнейшие закономерности полета космических аппаратов и определить основные характеристики их траекторий. К таким случаям относятся, в частности, полеты к Луне и другим планетам с помощью ракет на химических топливах.
Исходя из указанных предпосылок, рассмотрим задачу о полете к Луне.
Луна, являющаяся естественным спутником Земли, движется вокруг нее по орбите, близкой к круговой. Продолжительность одного оборота Луны вокруг Земли составляет примерно 27,3 суток. Расстояние ее от Земли составляет в среднем 384 400 км. Скорость движения Луны по орбите составляет примерно 1 км/сек. Двигаясь с такой скоростью, Луна описывает по небесной сфере в течение суток дугу около 13°. Плоскость орбиты Луны в настоящее время наклонена к плоскости земного экватора под углом примерно 18°.
Можно представить себе три основных вида полета космических аппаратов к Луне:
а) полет с попаданием космического аппарата в Луну;
б) облет Луны с возвращением к Земле;
в) пролет вблизи Луны с последующим выходом космического аппарата за пределы сферы действия Земли и превращением его в спутник Солнца - искусственную планету.
Каждый из указанных видов полета представляет самостоятельный интерес, позволяя решать определенный круг научных задач.
Исследование вопроса о минимальной скорости, необходимой для достижения Луны, показывает, что для сближения космического аппарата с Луной на первом обороте орбиты ему должна быть придана скорость, равная или большая некоторой величины V0min , зависящей от высоты в конце участка выведения. При высоте около 200 км V0min = Vпар - 95 м/сек (здесь -Vпар - параболическая скорость на данной высоте). Орбита космического аппарата при V0 = V0min представляет эллипс с апогеем, равным расстоянию от Земли до орбиты Луны.
Полет к Луне таким образом может быть осуществлен при различных значениях начальной скорости как меньших, так и больших параболической скорости. Соответственно и траектория полета космического аппарата до вхождения его в сферу действия Луны может быть эллиптической, параболической или гиперболической.
После того как космический аппарат достигнет границы сферы действия Луны, параметры его движения должны быть, в соответствии с приближенной методикой, пересчитаны в систему координат, связанную с центром Луны - в так называемую селеноцентрическую систему координат. Для этого вектор скорости космического аппарата V* нужно сложить с вектором, обратным вектору скорости центра Луны в геоцентрической системе координат Vл (рис. 13). Начало движения космического аппарата в селеноцентрической системе соответствует точке входа в сферу действия Луны В.
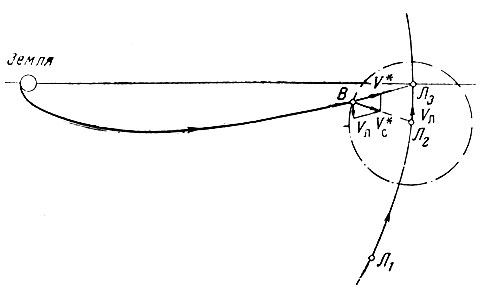
Рис. 13. Схема траектории полета к Луне, лежащей в плоскости лунной орбиты: Л1 - положение Луны в момент старта космического аппарата; Л2 - положение Луны в момент достижения космическим аппаратом границы сферы действия Луны; В - точка входа траектории в сферу действия Луны; Vл - скорость движения Луны по орбите; V* - скорость космического аппарата в точке В в геоцентрической системе координат; V*c - скорость космического аппарата в точке В в селеноцентрической системе координат; Л3 - положение Луны в момент сближения с ней космического аппарата
Можно показать, что траектория космического аппарата внутри сферы действия Луны в селеноцентрической системе координат всегда является гиперболической. Это объясняется тем, что при любом характере траектории полета от Земли до границы сферы действия Луны селеноцентрическая скорость космического аппарата на границе сферы действия по крайней мере вдвое превышает параболическую скорость относительно Луны, равную 0,383 км/сек. Вследствие этого любая траектория сближения, проходящая мимо Луны, должна выйти за пределы ее сферы действия*.
* (При использовании приближенной методики параметры движения космического аппарата в точке выхода из сферы действия Луны должны быть пересчитаны вновь в геоцентрическую систему координат.)
Из этого обстоятельства вытекает положение о невозможности захвата космического аппарата полем тяготения Луны. Для превращения космического аппарата в искусственный спутник Луны ему должна быть сообщена некоторая дополнительная скорость таким образом, чтобы скорость его движения в селеноцентрической системе стала меньшей, чем параболическая. Для этого космический аппарат должен быть снабжен ракетным двигателем, включаемым в период нахождения его в сфере действия Луны.
Наиболее благоприятно осуществление полета к Луне в случае, когда плоскость траектории космического аппарата совпадает с плоскостью лунной орбиты. Такой случай может быть реализован при осуществлении старта ракеты из экваториальных районов. В других случаях, когда старт ракеты производится со средних или полярных широт, и, в частности, в случае запуска с территории СССР, плоскость ее траектории не может совпасть с плоскостью орбиты Луны. Осуществление полетов к Луне в таких условиях является более трудной задачей и влечет за собой более высокие требования к энергетическим характеристикам и точности системы управления космической ракеты.
Остановимся на этом вопросе подробнее. Представим себе, что старт ракеты производится из северного полушария Земли и точка А, соответствующая концу участка выведения, расположена на широте ψг, а Луна в момент попадания находится в точке Л (рис. 14).
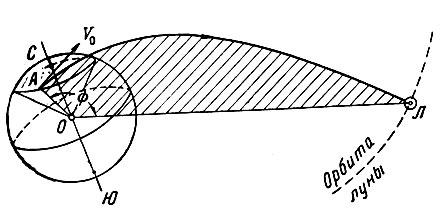
Рис. 14. Схема траектории полета к Луне при старте ракеты из северного полушария Земли: А - точка старта; V0 - скорость в конце участка выведения; Л - положение Луны в момент попадания; Ф - угловая дальность
Орбита космического аппарата, проходящая через точки А и Л, лежит в плоскости АОЛ, где О - центр Земли. Угол между направлениями О А и ОЛ носит название угловой дальности Ф. Величина его зависит от положения точки А, движущейся по параллели при вращении Земли, а также от положения Луны на ее орбите в момент попадания.
Наибольшее значение угла Ф имеет место, когда в момент встречи склонение Луны близко к -18° (Луна ниже плоскости экватора), а пуск ракеты осуществляется в момент нахождения Луны вблизи точки нижней кульминации (по отношению к точке старта). Соответственно наименьшее значение Ф имеет место, когда склонение Луны близко к +18°. Наиболее наглядно это можно проиллюстрировать для случая, когда плоскость орбиты космического аппарата совпадает с осью Земли, т. е. когда наклонение орбиты равно 90°. Максимальное значение Ф в этом случае составляет Ф = 180°+ 18° - ψг (рис. 15, а), а минимальное - Ф = 180°-18° - ψг (рис. 15, б).
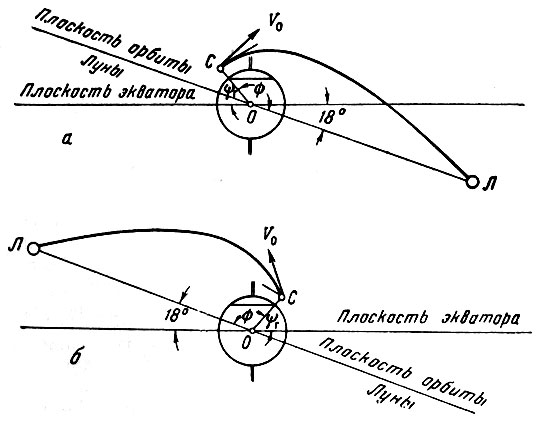
Рис. 15. Траектория полета к Луне: а - при минимальном значении склонения Луны в момент встречи; б - при максимальном значении склонения Луны в момент встречи (плоскость орбиты космического аппарата совпадает с осью Земли)
Рассмотрим теперь, как влияет величина угла Ф на условия полета к Луне. Из приведенных выше формул движения космического аппарата в центральном поле тяготения следует, что параметры его движения в конце участка выведения и в точке встречи однозначно связаны функциональной зависимостью:
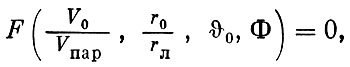 (1.36)
(1.36)
где V0 и Vпар - соответственно скорость космического аппарата и параболическая скорость в конце участка выведения; r0 и rл - расстояния от центра Земли до конца участка выведения и до орбиты Луны:  0 - угол наклона вектора скорости к горизонту в конце участка выведения.
0 - угол наклона вектора скорости к горизонту в конце участка выведения.
Поскольку отношение 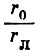 мало и практически постоянно, то при каждом данном значении
мало и практически постоянно, то при каждом данном значении 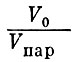 угол
угол  0 зависит только от Ф. На рис. 16 представлена зависимость
0 зависит только от Ф. На рис. 16 представлена зависимость  0 = f (Ф) при различных значениях V0 и h0 = 200 км. Как видно из графика, для всех значений скорости V0 величина
0 = f (Ф) при различных значениях V0 и h0 = 200 км. Как видно из графика, для всех значений скорости V0 величина  0 существенно уменьшается с увеличением Ф.
0 существенно уменьшается с увеличением Ф.
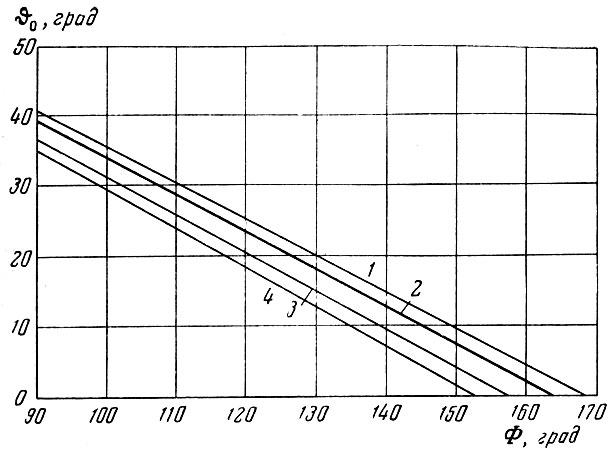
Рис. 16. Зависимость угла наклона вектора скорости
 0 от угловой дальности Ф: 1 - при V0 = Vпар - 50 м/сек; 2 - при V0 = Vпар; 3 - при V0 = Vпар + 100 м/сек; 4 - при V0 = Vпар + 200 м/сек
0 от угловой дальности Ф: 1 - при V0 = Vпар - 50 м/сек; 2 - при V0 = Vпар; 3 - при V0 = Vпар + 100 м/сек; 4 - при V0 = Vпар + 200 м/сек
Уменьшение же  0, т. е. переход к более пологим траекториям выведения, влечет за собой снижение потерь на преодоление сил тяжести
0, т. е. переход к более пологим траекториям выведения, влечет за собой снижение потерь на преодоление сил тяжести 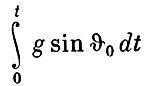 и позволяет увеличить вес полезного груза ракеты.
и позволяет увеличить вес полезного груза ракеты.
Из сказанного следует, что при старте космической ракеты со средних широт северного полушария энергетически наиболее выгодно осуществлять пуск ракеты в период, когда Луна находится вблизи точки своей орбиты с минимальным склонением. В этом случае обеспечивается возможность выведения на орбиту максимального полезного груза. При осуществлении пуска в более ранние или более поздние сроки возможный вес полезного груза уменьшается. Однако при отклонении даты пуска от оптимальной даты на несколько дней уменьшение веса полезного груза сравнительно невелико. Практически в течение каждого лунного месяца можно указать интервал времени, продолжительностью около недели, в пределах которого условия полета к Луне являются благоприятными. При больших отклонениях даты пуска от оптимальной имеет место значительное уменьшение возможного веса полезного груза ракеты.
Продолжительность полета космического аппарата до сближения с Луной определяется величиной его скорости по отношению к параболической скорости (рис. 17). При минимальном значении начальной скорости (V0 = V0min) продолжительность полета составляет немного более четырех суток, при скорости равной параболической (V0 = Vпар),- около двух суток, а при скорости, превышающей параболическую на 500 м/сек, - примерно одни сутки.
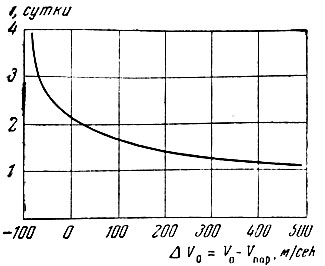
Рис. 17. Продолжительность полета космического аппарата до встречи с Луной (h0 = 200 км)
При осуществлении полетов к Луне в большинстве случаев необходимо вести наблюдения за космическим аппаратом и прием телеметрической информации в период сближения аппарата с Луной и в момент их встречи. Для этого нужно, чтобы Луна в этот период времени находилась по отношению к наблюдательным пунктам вблизи точки верхней кульминации. В то же время, как показано выше, энергетически выгодно осуществлять пуск ракеты в то время, когда Луна находится вблизи точки нижней кульминации по отношению к точке старта. Очевидно, что оба эти условия могут быть выполнены только в том случае, если продолжительность полета кратна полусуткам, т. е. равна полусуткам, полутора суткам, двум с половиной суткам и т. д. Наиболее благоприятным является вариант полета продолжительностью около полутора суток, для осуществления которого скорость космического аппарата в конце участка выведения должна несколько превышать параболическую скорость (приблизительно на 150 м/сек). Вариант полета продолжительностью около полусуток требует значительного превышения скорости в конце участка выведения над параболической скоростью, а варианты полета продолжительностью двое с половиной и более суток связаны с необходимостью более точного выведения космического аппарата на орбиту для попадания в Луну.
Для осуществления облета Луны с возвращением к Земле скорость космического аппарата в конце участка выведения должна быть меньше параболической. В зависимости от степени сближения с Луной можно различать два основных вида такого полета - далекий и близкий облет Луны.
При далеком облете, когда минимальное расстояние космического аппарата от Луны составляет 40 тыс. км и более, влияние поля тяготения Луны на движение космического аппарата невелико, и его орбита в геоцентрической системе близка к эллипсу. Если старт ракеты осуществляется со средних широт, то угол наклона вектора скорости в конце участка выведения существенно отличен от нуля и, следовательно, эллиптическая орбита пересекается с поверхностью Земли. В результате космический аппарат в конце первого оборота по орбите должен войти в плотные слои атмосферы и разрушиться.
Особый интерес представляет случай так называемого близкого облета, когда минимальное расстояние космического аппарата от Луны составляет около 5-10 тыс. км. В этом случае оказывается возможным, используя воздействие силы притяжения Луны, изменить характер орбиты космического аппарата в период первого его сближения с Луной таким образом, чтобы получить новую орбиту, отвечающую заданным требованиям. В частности, можно обеспечить такое изменение орбиты, чтобы космический аппарат превратился в искусственный спутник Земли, движущийся по орбите с перигеем, равным нескольким десяткам тысяч километров, и апогеем, достигающим полумиллиона километров. Примером такого варианта полета к Луне является полет третьей советской космической ракеты с автоматической межпланетной станцией.
Перейдем к рассмотрению случаев, когда траектория космического аппарата выходит за пределы сферы действия Земли. В этих случаях скорость в конце участка выведения превышает параболическую или равна ей, а траектория в пределах сферы действия Земди является гиперболической или параболической.
Скорость космического аппарата на границе сферы действия Земли V*, как видно из формулы (1.18), однозначно определяется скоростью V0 и высотой h0 в конце участка выведения. Зависимость V* от V0 при h0 = 200 км приведена на рис. 18. При скорости в конце участка выведения, равной параболической (V0 = Vпар), скорость на границе сферы действия
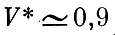
. Увеличение V0 на 0,5 км/сек по отношению к Vпар приводит к возрастанию V* до 3,3 км/сек, а на 1 км/сек - до 4,9 км/сек. При скоростях, близких к параболической, увеличение V0 на 1 м/сек приводит к возрастанию V* на 5-8 м/сек.
Движение космического аппарата после выхода за пределы сферы действия Земли можно рассчитать, исходя из параметров его движения в точке выхода. Скорость космического аппарата в гелиоцентрической системе может быть получена суммированием вектора скорости 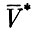 и вектора скорости центра Земли в соответствующий момент времени
и вектора скорости центра Земли в соответствующий момент времени 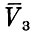 . Полученный вектор скорости
. Полученный вектор скорости 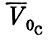 и определит характер движения космиче-ского аппарата в гелиоцентрической системе.
и определит характер движения космиче-ского аппарата в гелиоцентрической системе.
Если V0c меньше параболической скорости относительно Солнца V парс, то движение космического аппарата в солнечной системе будет происходить по эллиптической орбите, и он превратится в спутник Солнца - искусственную планету. Если же V0с равно параболической скорости Vпарc или превышает ее, то движение космического аппарата будет происходить по параболической или гиперболической траектории. В этих случаях он навсегда покинет пределы солнечной системы. Определим, какая минимальная скорость для этого должна быть сообщена космическому аппарату при отлете с Земли. Средняя скорость движения Земли по своей орбите составляет V3 = 29,75 км/сек и, следовательно, параболическая скорость относительно Солнца, вычисленная с учетом среднего радиуса земной орбиты, равна 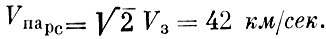 .
.
Представим себе, что вектор скорости космического аппарата на границе сферы действия параллелен вектору скорости движения Земли по орбите, что может быть обеспечено соответствующим выбором направления пуска космического аппарата. При этом условии космический аппарат будет двигаться в гелиоцентрической системе с параболической скоростью, если его скорость в геоцентрической системе составит V* = Vпарс - V3 = 12,25 км/сек, для чего скорость его в конце участка выведения, как это видно из графика рис. 18, должна быть равной примерно 16,5 км/сек.
Скорость, обеспечивающая вылет космического аппарата за пределы поля тяготения Солнца, носит название третьей космической скорости. Значение третьей космичеcкой скорости при высоте h0 = 0, т. е. у поверхности Земли, составляет около 16,7 км/сек.
Рассмотрим более подробно движение космических аппаратов в солнечной системе по эллиптическим орбитам и, в частности, полеты к другим планетам. При этом в качестве первого приближения будем считать, что движение Земли и других планет происходит по круговым орбитам, радиусы которых соответствуют средним радиусам их действительных орбит. Будем считать также, что орбиты всех планет и траектории космических аппаратов лежат в одной плоскости.
Представим себе, что траектория полета космического аппарата в сфере действия Земли выбрана таким образом, что вектор скорости на границе сферы действия 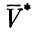 параллелен вектору скорости Земли по орбите
параллелен вектору скорости Земли по орбите 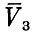 . При этом, если направления их совпадают, то скорость космического аппарата в гелиоцентрической системе равна их арифметической сумме и будет максимальной для данного значения скорости V*0. Орбита космического аппарата в гелиоцентрической системе в этом случае будет охватывать орбиту Земли, касаясь ее в перигелии, удаленном от Солнца на расстояние радиуса земной орбиты rπ = r3. Расстояние от Солнца до афелия орбиты rα будет зависеть от скорости космического аппарата. Значения га в зависимости от скорости в конце участка выведения V0 при h0 = 200 км приведены в табл. 12.
. При этом, если направления их совпадают, то скорость космического аппарата в гелиоцентрической системе равна их арифметической сумме и будет максимальной для данного значения скорости V*0. Орбита космического аппарата в гелиоцентрической системе в этом случае будет охватывать орбиту Земли, касаясь ее в перигелии, удаленном от Солнца на расстояние радиуса земной орбиты rπ = r3. Расстояние от Солнца до афелия орбиты rα будет зависеть от скорости космического аппарата. Значения га в зависимости от скорости в конце участка выведения V0 при h0 = 200 км приведены в табл. 12.
| Скорость в конце участка выведения, км/сек | Превышение скорости над параболической, км/сек | Расстояние от Солнца до афелия орбиты, млн. км |
|---|---|---|
| 11,015 | 0 | 168,5 |
| 11,515 | 0,5 | 247,7 |
| 12,015 | 1,0 | 314,1 |
| 13,015 | 2,0 | 480,1 |
| 14,015 | 3,0 | 760,3 |
| 15,015 | 4,0 | 1400,0 |
| 16,015 | 5,0 | 4618,0 |
Из данных таблицы видно, что при скорости космического аппарата превышающей параболическую на 0,5 км/сек, афелий его гелиоцентрической орбиты будет расположен за орбитой Марса, при скорости, превышающей параболическую на 3 км/сек, он будет находиться вблизи орбиты Юпитера, а при скорости, превышающей параболическую на 4 км/сек,- достигнет орбиты Сатурна.
Если направление вектора скорости космического аппарата на границе сферы действия противоположно вектору скорости Земли, то скорость его в гелиоцентрической системе равна их разности и будет минимальной для данного значения V0*. В этом случае орбита космического аппарата будет расположена внутри орбиты Земли, касаясь ее в афелии (rα = r3).
Расстояния от Солнца до перигелия орбиты такого типа в зависимости от скорости космического аппарата в конце участка выведения V0 при h0= 200 км даны в табл. 13.
| Скорость в конце участка выведения, км/сек | Превышение скорости над параболической, км/сек | Расстояние от Солнца до афелия орбиты, млн. км |
|---|---|---|
| 11,015 | 0 | 132,8 |
| 11,515 | 0,5 | 95,6 |
| 12,015 | 1,0 | 80,3 |
| 13,015 | 2,0 | 61,8 |
| 14,015 | 3,0 | 49,8 |
| 15,015 | 4,0 | 40,9 |
| 16,015 | 5,0 | 33,9 |
Как видно из таблицы, при скорости космического аппарата V0, превышающей параболическую на 2 км/сек, перигелий его орбиты будет расположен вблизи орбиты Меркурия. Для приближения орбиты космического аппарата к Солнцу на близкие расстояния необходимо придать ему в конце участка выведения весьма большую скорость. Так, для приближения к Солнцу на расстояние, равное 30 млн. км, космическому аппарату необходимо сообщить скорость 16,7 км/сек, превышающую третью космическую скорость.
Таким образом, приближение к Солнцу на близкие расстояния энергетически является более сложной задачей, чем вылет за пределы поля тяготения Солнца.
Рассматриваемые орбиты космических аппаратов могут быть использованы для полетов к другим планетам солнечной системы. Минимально необходимая для полета к данной планете скорость космического аппарата будет соответствовать полуэллиптической орбите, которая в своем афелии и перигелии касается орбит Земли и планеты назначения. Угловая дальность орбитального участка полета космического аппарата в гелиоцентрической системе при этом будет составлять Ф1 = 180°(рис. 19 и 20).
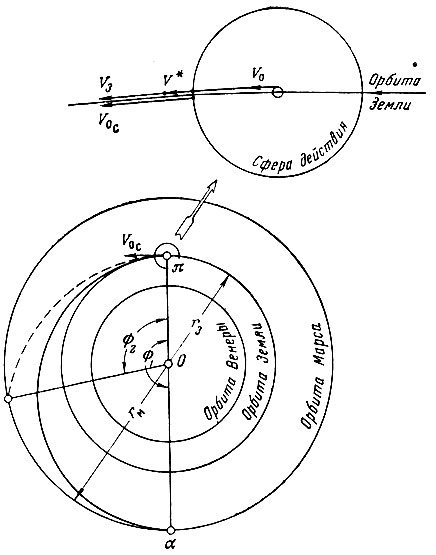
Рис. 19. Траектории полета к Марсу: О - Солнце; r3 - средний радиус орбиты Земли; rм - средний радиус орбиты Марса; V0 - скорость космического аппарата в конце участка выведения; V3 - скорость движения Земли по орбите; V0c - скорость космического аппарата на границе сферы действия Земли в геоцентрической системе; V0 - скорость аппарата на границе сферы действия Земли в гелиоцентрической системе (начальная скорость для гелиоцентрической орбиты); π - перигелий гелиоцентрической орбиты; α - афелий гелиоцентрической орбиты; Ф1 Ф2 - угловая дальность для гелиоцентрических орбит
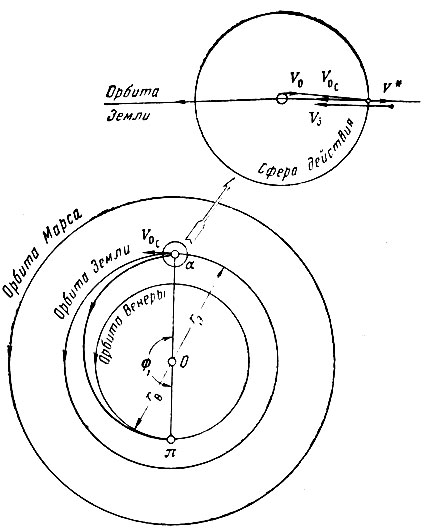
Рис. 20. Траектории полета к Венере: 0 - Солнце; r3 - средний радиус орбиты Земли; rв - средний радиус орбиты Венеры; V0 - скорость космического аппарата в конце участка выведения; Vз - скорость движения Земли по орбите; V* - скорость космического аппарата на границе сферы действия Земли в геоцентрической системе; V0c - скорость аппарата на границе сферы действия Земли в гелиоцентрической системе (начальная скорость для гелиоцентрической орбиты); π - перигелий гелиоцентрической орбиты; α - афелий гелиоцентрической орбиты; Ф1 - угловая дальность
Значения необходимых скоростей для полетов к другим планетам по полуэллиптическим орбитам и продолжительность таких полетов, вычисленные для средних радиусов орбит планет, в предположении, что все орбиты лежат в одной плоскости, приведены в табл. 14.
| Планета | Скорость в конце участкавыведения, км/сек | Продолжительность полета до встречи с планетой, год |
|---|---|---|
| Меркурий | 13,31 | 0,29 |
| Венера | 11,25 | 0,40 |
| Марс | 11,35 | 0,71 |
| Юпитер | 14,05 | 2,72 |
| Сатурн | 15,03 | 6,04 |
| Уран | 15,73 | 16,0 |
| Нептун | 16,00 | 30,6 |
При увеличении скорости V0 по сравнению с минимально необходимой пересечение орбиты космического аппарата с орбитой планеты происходит при меньшем значении угловой дальности Ф2 < Ф1. Одновременно уменьшается продолжительность полета. Основные данные таких орбит для случаев полета к Марсу и Венере приведены в табл. 15 и 16.
| Начальная скорость, для гелиоцентрической орбиты, км/сек | Угловая дальность град | Продолжительность полета, мес. |
|---|---|---|
| 32,71 | 180 | 8,63 |
| 33,71 | 124 | 5,25 |
| 34,71 | 108 | 4,32 |
| 35,71 | 97 | 3,77 |
| 36,71 | 90 | 3,40 |
| 37,71 | 85 | 3,10 |
| Начальная скорость, для гелиоцентрической орбиты, км/сек | Угловая дальность град | Продолжительность полета, мес. |
|---|---|---|
| 27,28 | 180 | 4,87 |
| 26,28 | 110 | 3,33 |
| 25,28 | 89 | 2,83 |
| 24,28 | 76 | 2,52 |
| 23,28 | 66 | 2,33 |
| 22,28 | 59 | 2,16 |
Для обеспечения встречи космического аппарата с планетой момент его пуска должен быть выбран таким образом, чтобы взаимное расположение Земли в момент старта и планеты в момент встречи с ней космического аппарата было бы вполне определенным.
Благоприятные для полетов взаимные расположения планет периодически повторяются. Для полетов к Марсу период их повторения составляет 2,14 года, а для полетов к Венере - 1,57 года.
Следует отметить, что приведенные данные о необходимой скорости для полетов к планетам, вследствие сделанных при расчетах допущений, являются ориентировочными и характеризуют нижний предел потребных скоростей. Они справедливы для случаев, когда встреча космического аппарата с планетой происходит вблизи узла ее орбиты, т. е. когда движение космического аппарата происходит в плоскости эклиптики.
В других случаях, соответствующих встрече космического аппарата с планетой в периоды, когда она не находится в плоскости эклиптики (в связи с тем, что плоскость ее орбиты составляет некоторый угол с плоскостью эклиптики), скорость, необходимая для полета к планете, может оказаться значительно большей.
В заключение рассмотрим вопрос о создании искусственных спутников Солнца (искусственных планет), движущихся по круговым орбитам. Для этого космический аппарат должен быть сначала выведен на полуэллиптическую переходную орбиту, касающуюся в афелии или перигелии заданной круговой орбиты. При достижении космическим аппаратом афелия (или перигелия) переходной орбиты ему должна быть сообщена дополнительная скорость ДУ, обеспечивающая его переход на круговую орбиту (рис. 21).
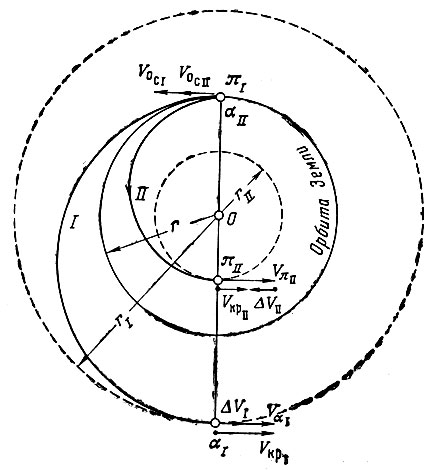
Рис. 21. Траектории перехода космического аппарата на круговые орбиты вокруг Солнца: 0 - Солнце; V0СI . V0cII -скорость космического аппарата на границе сферы действия Земли в гелиоцентрической системе; VαI, VπII - скорость космического аппарата в точке перехода на круговую орбиту вокруг Солнца; ΔVI, ΔVII - дополнительная скорость, которую нужно сообщить космическому аппарату для перехода на круговую орбиту; VкрI VкрII - круговая скорость; rI , rII -радиус круговой орбиты; r -средний радиус орбиты Земли. Индекс I относится к случаю перехода космического аппарата на орбиту большого радиуса, чем радиус орбиты Земли, индекс II - к случаю перехода на орбиту меньшего радиуса, чем радиус орбиты Земли
Примерные значения суммарной скорости Fo + ЛУ" которую нужно сообщить космическому аппарату для превращения его в искусственную планету, движущуюся по круговой орбите, приведены в табл. 17.
| Радиус круговой орбиты, млн.км | Суммарная скорость, км/сек |
|---|---|
| 58 (орбита Меркурия) | 23,0 |
| 108 (орбита Венеры) | 14,0 |
| 228 (орбита Марса) | 14,0 |
| 778 (орбита Юпитера) | 19,7 |
| 1426 (орбита Сатурна) | 20,5 |
| 2869 (орбита Урана) | 20,4 |
| 4495 (орбита Нептуна) | 20,1 |
Требования к точности параметров движении в конце участка выведения
Для осуществления полета космического аппарата по заданной орбите ему должны быть приданы вполне определенные параметры движения. Даже незначительные погрешности в величине и направлении скорости в конце, участка выведения могут привести к заметным отклонениям орбиты космического аппарата от расчетной.
Покажем, насколько существенно влияют эти погрешности на характеристики орбит и время существования искусственных спутников Земли.
Для иллюстрации сказанного в табл. 18 приведены данные, характеризующие изменение основных параметров орбиты искусственного спутника - высоты перигея и апогея - при наличии погрешностей по скорости и углу наклона касательной к траектории в конце участка выведения (рассмотрен случай выведения спутника в перигей орбиты).
| Исходные параметры орбиты: | |||||
| высота перигея, км... | 250 | 250 | 250 | 250 | 250 |
| высота апогея, км... | 800 | 1500 | 5000 | 15000 | 30000 |
| Изменения параметров орбиты при погрешности по скорости выведения ± 10 м/сек | |||||
| изменение высоты перинея, км... | 0 | 0 | 0 | 0 | 0 |
| изменение высоты апогея, км | ± 39 | ± 40 | ± 73 | ± 190 | ± 472 |
| Изменение параметров орбиты при погрешности по углу выведения ± 1° | |||||
| изменения высоты перигея, км... | -25 | -13 | -4,8 | -2,8 | 2,5 |
| изменение высоты апогея, км... | +25 | +13 | +4,8 | +2,8 | +2,5 |
Из таблицы видно, что погрешность по скорости вызывает соответствующее изменение высоты апогея и периода обращения спутника, не сказываясь на высоте перигея. При этом для низких орбит величина изменения высоты апогея весьма слабо зависит от исходных значений параметров орбиты. Однако при увеличении высоты орбиты влияние погрешностей по скорости на высоту апогея и период обращения спутника заметно возрастает.
Погрешность по углу выведения всегда приводит к уменьшению высоты перигея и к такому же увеличению высоты апогея. Поскольку торможение спутника происходит в основном в области перигея, это приводит к сокращению времени существования спутника.
Для орбиты с высотой апогея 800 км при высоте перигея 250 км погрешность по углу в конце участка выведения, равная 1°, приводит к понижению перигея на 25 км, что вызывает сокращение времени существования спутника в 2 раза.
Влияние погрешностей по углу выведения на высоту перигея уменьшается с увеличением эксцентриситета орбиты, т. е. с возрастанием высоты апогея при неизменной высоте перигея. Так, для орбиты с указанной выше высотой перигея (250 км) и высотой апогея 1500 км понижение перигея за счет той же ошибки по углу выведения составляет 13 км. Время существования спутника в этом случае сокращается за счет погрешности по углу выведения, равной 1°, только в 1,5 раза. Следовательно, для более вытянутых орбит уменьшение времени существования спутника за счет погрешностей выведения будет меньше, чем для орбит, близких к круговым.
На период обращения погрешности по углу не влияют, поскольку величина большой оси эллиптической орбиты при этом не меняется.
Покажем теперь, какое влияние оказывают погрешности в конце участка выведения на орбиты космических аппаратов, предназначенных для полета к Луне. Остановимся сначала на наиболее благоприятном случае, когда орбита космического аппарата лежит в плоскости лунной орбиты. Такой случай, как указано выше, может быть реализован при запуске ракеты из экваториальных районов.
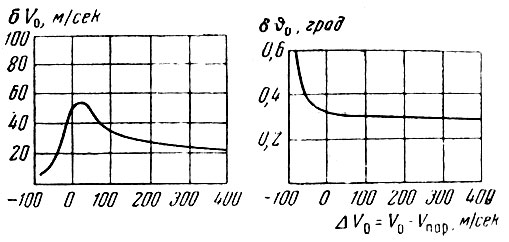
Предположим, что расчетная орбита проходит через центр Луны. На рис. 22 приведены значения предельных погрешностей по скорости δV0 и по углу δ 0 (соответствующих отклонению орбиты от центра до края Луны*). Из графиков следует, что значения предельных погрешностей δV0 и δ
0 (соответствующих отклонению орбиты от центра до края Луны*). Из графиков следует, что значения предельных погрешностей δV0 и δ 0 существенно изменяются в зависимости от избытка скорости в конце участка выведения по отношению к местной параболической скорости ΔV0 = V0 - Vпар.
0 существенно изменяются в зависимости от избытка скорости в конце участка выведения по отношению к местной параболической скорости ΔV0 = V0 - Vпар.
* (См. Успехи физических наук, 1957, т. LXIII, вып. 1а, стр. 101.)
 0 при попадании в Луну (Случай, когда орбита космического аппарата лежит в плоскости лунной орбиты)">
0 при попадании в Луну (Случай, когда орбита космического аппарата лежит в плоскости лунной орбиты)">Рис. 22. Значения предельных погрешностей по скорости δV0 и по углу δ
 0 при попадании в Луну (Случай, когда орбита космического аппарата лежит в плоскости лунной орбиты)
0 при попадании в Луну (Случай, когда орбита космического аппарата лежит в плоскости лунной орбиты)
При скоростях, меньших чем параболические на 50-60 м/сек, т. е. при эллиптических орбитах, предельные ошибки составляют: δV0≈ 10 м/сек и δ 0 = 0,4°. При скоростях больших, чем параболические, - при гиперболических орбитах - предельная погрешность по скорости возрастает до 20-40 м/сек, а предельная погрешность по углу уменьшается до 0,3°. Учитывая, однако, что отклонения орбиты определяются совместным влиянием погрешностей по скорости и углу, а также принимая во внимание наличие других погрешностей, приводящих к отклонениям орбиты, можно считать, что в случае гиперболических орбит, лежащих в плоскости лунной орбиты, погрешности в конце участка выведения не должны превышать: по скорости 10-20 м/сек, по углу 0,15-0,20°.
0 = 0,4°. При скоростях больших, чем параболические, - при гиперболических орбитах - предельная погрешность по скорости возрастает до 20-40 м/сек, а предельная погрешность по углу уменьшается до 0,3°. Учитывая, однако, что отклонения орбиты определяются совместным влиянием погрешностей по скорости и углу, а также принимая во внимание наличие других погрешностей, приводящих к отклонениям орбиты, можно считать, что в случае гиперболических орбит, лежащих в плоскости лунной орбиты, погрешности в конце участка выведения не должны превышать: по скорости 10-20 м/сек, по углу 0,15-0,20°.
При осуществлении пуска ракеты к Луне со средних широт, например, с территории СССР, требования к точности параметров движения, необходимой для попадания в Луну, значительно возрастают.
Так, для гиперболической орбиты, по которой происходило движение второй советской космической ракеты, погрешность в скорости, равная 1 м/сек, приводит к отклонению точки встречи с Луной на 250 км. Отклонение вектора скорости от его расчетного направления на одну угловую минуту вызывает смещение точки встречи на 200 км.
На отклонение точки встречи оказывают также существенное влияние погрешности координат конца участка выведения и неточность времени старта ракеты. При отличии момента старта от расчетного на 10 сек имеет место отклонение точки встречи на поверхности Луны порядка 200 км.
Исходя из приведенных цифр, можно считать, что при пуске ракеты с территории СССР для попадания в Луну погрешность скорости в конце участка выведения не должна превышать нескольких метров в секунду, а отклонения вектора скорости от его расчетного направления не должны быть более 0,1°.
Еще большее влияние оказывают погрешности выведения на орбиты космических аппаратов при осуществлении полетов к другим планетам. Так" при полете к Марсу по эллиптической орбите, обеспечивающей сближение с Марсом в афелии, погрешность по скорости в конце участка выведения, равная 1 м/сек, вызывает отклонение орбиты космического аппарата вблизи Марса порядка 30 тыс. км. В связи с этим при таких полетах движение космического аппарата должно корректироваться в процессе самого полета.
Космические ракеты и ракеты-носители искусственных спутников. Выведение на орбиту
Как уже отмечалось, основной проблемой, связанной с запуском космического аппарата, является выведение на орбиту - придание ему на соответствующей высоте скорости, равной или превышающей первую космическую скорость.
Основным средством для решения этой задачи в настоящее время являются многоступенчатые ракеты с жидкостными реактивными двигателями, работающими на химическом топливе*. В более или менее близком будущем можно ожидать появления космических ракет с реактивными двигателями, использующими ядерную энергию.
* (В некоторых случаях космическая ракета может иметь от дельные ступени с двигателями, работающими на твердом топливе (порохе).)
Многоступенчатая (или составная) ракета, идея создания которой впервые была выдвинута К. Э. Циолковским, состоит из ряда последовательно соединенных ракет. Рассмотрим ее схему на примере трехступенчатой ракеты, изображенной на рис. 23. Каждая из трех ракет имеет свой двигатель и топливные баки для горючего и окислителя. Первая ступень включает в себя все три ракеты, причем вторая и третья ракеты являются своего рода полезным грузом первой ракеты. По окончании работы двигателя первой ракеты она отделяется и дальнейший полет продолжает вторая ступень, состоящая из второй и третьей ракет. По окончании работы двигателя второй ракеты она также отделяется, после чего полет продолжает одна третья ракета (третья ступень).
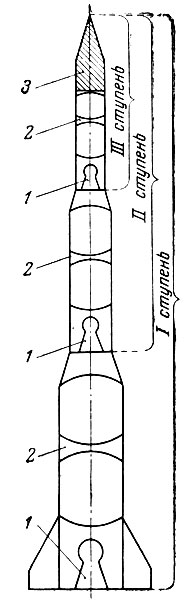
Рис. 23. Схема трехступенчатой ракеты: 1 - двигатели; 2 - топливные баки; 3 - полезный груз (космический аппарат)
Таким образом, в многоступенчатой ракете по мере использования топлива происходит отделение соответствующих частей ее конструкции. Вследствие этого ускорение ее, при том же значении реактивной силы, оказывается большим, чем у одноступенчатой ракеты, обладающей такими же характеристиками. В результате ракета приобретает большую скорость.
Схема траектории выведения спутника на орбиту приведена на рис. 24. Угол наклона вектора скорости к горизонту в данной точке траектории обозначен через  . Старт ракеты-носителя осуществляется вертикально (
. Старт ракеты-носителя осуществляется вертикально ( н = 90°). Затем, после небольшого участка вертикального подъема, ракета начинает постепенно поворачиваться относительно поперечной оси по определенной программе, в результате чего траектория ее движения искривляется. Выбирая соответствующую программу разворота ракеты по времени, можно получить требуемые значения высоты и угла в конце участка выведения h0 и
н = 90°). Затем, после небольшого участка вертикального подъема, ракета начинает постепенно поворачиваться относительно поперечной оси по определенной программе, в результате чего траектория ее движения искривляется. Выбирая соответствующую программу разворота ракеты по времени, можно получить требуемые значения высоты и угла в конце участка выведения h0 и  0.
0.
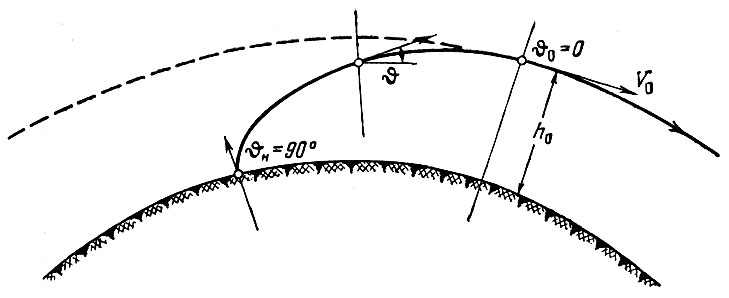
Рис. 24. Схема траектории выведения спутника на орбиту
При выведении спутника на орбиту  0 = 0 (рис. 24). При запуске космических аппаратов к Луне или другим планетам угол
0 = 0 (рис. 24). При запуске космических аппаратов к Луне или другим планетам угол  0, как правило, не равен нулю и определяется условиями пуска - датой пуска, взаимным расположением планет, географической широтой точки старта и др.
0, как правило, не равен нулю и определяется условиями пуска - датой пуска, взаимным расположением планет, географической широтой точки старта и др.
Проанализируем, какими основными факторами определяется скорость многоступенчатой ракеты в конце участка выведения. Для этого рассмотрим уравнение движения ракеты в проекции на касательную к траектории, имеющее вид:
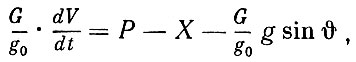 (1.37)
(1.37)где: G- текущее значение веса ракеты;
dV/dt - ускорение движения ракеты;
g - ускорение силы тяжести;
g0 - ускорение силы тяжести на поверхности Земли (на уровне моря);
P - реактивная тяга;
X - сила аэродинамического сопротивления;

- угол наклона вектора скорости к горизонту.
Тяга ракеты может быть выражена в виде:
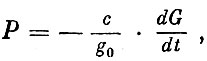 (1.38)
(1.38)где: с - скорость истечения реактивной струи;
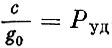
- удельная тяга двигателя;
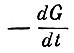
- расход топлива (изменение веса ракеты в единицу времени).
Тогда уравнение (1.37) можно представить в виде:
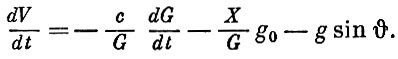 (1.39)
(1.39)Проинтегрировав уравнение в пределах от момента старта (t = 0) до момента, соответствующего концу участка выведения (t - tK), получим скорость ракеты в конце участка выведения:
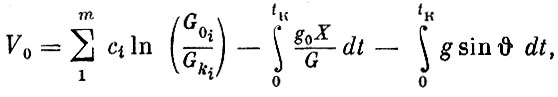 (1.40)
(1.40)где m - число ступеней, сi, G0i, Gki соответственно, скорость истечения, начальный и конечный вес для отдельных ступеней.
Первый член в правой части уравнения (1.40) соответствует формуле Циолковского и определяет скорость ракеты при отсутствии воздействия на нее каких-либо внешних сил - так называемую характеристическую скорость ракеты. Второй член в правой части уравнения характеризует потери в скорости на преодоление сил аэродинамического сопротивления, а третий член - потери в скорости, связанные с влиянием силы тяжести. Потерями скорости от несовпадения направления силы тяги и вектора скорости (угла атаки) мы пренебрегли при написании уравнения (1.37), ввиду их сравнительной малости.
При выведении космического аппарата на орбиту суммарная величина потерь скорости, связанных с влиянием силы тяжести и аэродинамического сопротивления, составляет в среднем около 2000-3000 м/сек. Таким образом, для придания спутнику скорости порядка 8000 м/сек ракета-носитель должна обладать характеристической скоростью около 10 000-11 000 м/сек, а для придания космическому аппарату скорости порядка 11 000 м/сек - характеристической скоростью около 13 000-14000 м/сек.
Характеристическая скорость многоступенчатой ракеты, как видно из уравнения (1.40), равна сумме произведений скоростей истечения на натуральные логарифмы от отношений начальных и конечных весов для отдельных ступеней.
Если принять, что скорость истечения с для всех ступеней одинакова и относительные веса конструкции для каждой из ступеней
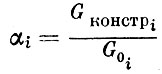
равны между собой (α1 = α2 = ... = αm-1 = αm = α), то можно показать, что в оптимальном случае, обеспечивающем максимум характеристической скорости, начальные веса ступеней должны быть распределены по закону геометрической прогрессии:
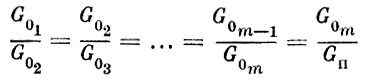 (1.41)
(1.41)или
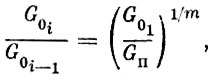
где: G01, G02...G0m - начальные веса ступеней, Сп -вес полезного груза (космического аппарата). Начальный вес первой ступени равен общему начальному весу ракеты С0l = С0.
Характеристическая скорость такой многоступенчатой ракеты может быть выражена формулой:
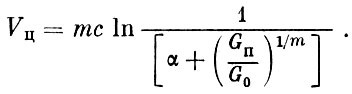 (1.42)
(1.42)
Взаимосвязь между параметрами, входящими в эту формулу, удобно представить в виде графика относительной характеристической скорости 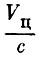 в зависимости от отношения начального веса ракеты к весу полезного груза
в зависимости от отношения начального веса ракеты к весу полезного груза 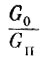 при различном числе ступеней m. Подобные графики приведены на рис. 25.
при различном числе ступеней m. Подобные графики приведены на рис. 25.
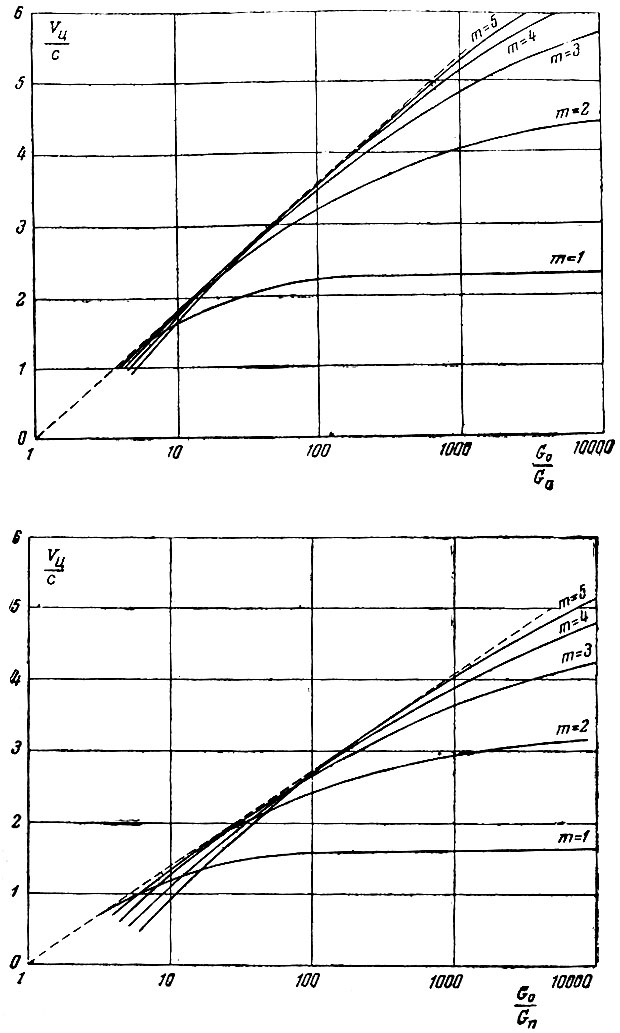
Рис. 25. Относительная характеристическая скорость ракет с различным числом ступеней в зависимости от отношения начального веса к весу полезного груза вверху - при α = 0,10; внизу - при α = 0,20
Из графиков видно, что в зависимости от значения 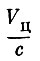 имеет место то или иное оптимальное число ступеней, обеспечивающее минимальное отношение веса ракеты к весу ее полезного груза. Вместе с тем из графиков следует, что одноступенчатая ракета (m = 1) практически не может обеспечить получение скорости, необходимой для выведения спутника на орбиту, если не ориентироваться на скорость истечения, превышающую 5000 м/сек, что для современных ракет на химическом топливе является нереальным.
имеет место то или иное оптимальное число ступеней, обеспечивающее минимальное отношение веса ракеты к весу ее полезного груза. Вместе с тем из графиков следует, что одноступенчатая ракета (m = 1) практически не может обеспечить получение скорости, необходимой для выведения спутника на орбиту, если не ориентироваться на скорость истечения, превышающую 5000 м/сек, что для современных ракет на химическом топливе является нереальным.
Семейство кривых, соответствующее ракетам с различным числом ступеней, имеет огибающую (пунктирная прямая на рис. 25). Можно показать, что предельные значения характеристической скорости, отвечающие такой огибающей, могут быть выражены формулой:
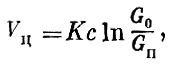 (1.43)
(1.43)где значения К зависят от относительного веса конструкции (рис. 26).
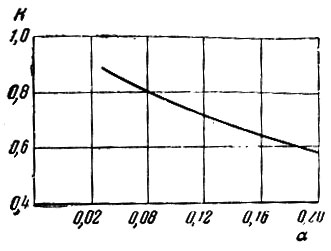
Рис. 26. Значение коэффициента К в зависимости от α
Из приведенной формулы очевидно, что предельная скорость ракеты при оптимальном выборе ее параметров зависит от отношения ее начального веса к весу полезного груза, скорости истечения реактивной струи и относительного веса конструкции. При этом начальный вес ракеты, обеспечивающей выведение на орбиту космического аппарата определенного веса, как видно из графиков на рис. 25, может находиться в весьма широких пределах, в зависимости от конкретных значений скорости истечения и относительного веса конструкции.
При выведении спутника на орбиту с заданной высотой перигея и апогея движение его на орбите может быть начато, вообще говоря, с любой точки орбиты. Необходимо лишь вывести спутник на высоту, отвечающую выбранной точке орбиты, и сообщить ему необходимую скорость в направлении касательной к орбите в этой точке. При этом, чем более высокая точка орбиты будет выбрана, тем меньшую скорость необходимо будет ему сообщить. Минимальная скорость должна быть сообщена спутнику, если движение его по орбите начинается в точке апогея.
Из сказанного, однако не следует делать вывод о целесообразности выведения спутника в апогей орбиты. Анализ этого вопроса показывает, что дополнительные энергетические затраты, связанные с подъемом спутника на большую высоту, превышают энергетический выигрыш от того, что спутнику в данном случае нужно сообщить меньшую скорость. Поэтому с точки зрения энергетических затрат наиболее рациональным оказывается выведение спутника на орбиту в области ее перигея.
При относительно малой высоте перигея заданной орбиты (порядка сотен километров) выведение на нее спутника может осуществляться непосредственно в конце активного участка траектории ракеты-носителя, как показано на рис. 24. С увеличением высоты точки выведения возрастают и энергетические затраты, связанные с влиянием силы тяжести на участке выведения.
Для высоких орбит, когда высота перигея может достигать многих тысяч километров, такой способ выведения вообще не может быть применен из-за ограниченности длины активного участка траектории. В этом случае спутник сначала должен быть выведен на некоторую переходную орбиту, имеющую достаточно низкий перигей. В некоторой точке переходной орбиты ракета-носитель должна сообщить спутнику дополнительную скорость, обеспечивающую переход его на заданную орбиту. Таким образом, траектория выведения в этом случае будет состоять из двух активных участков, разделенных участком полета по инерции.
Анализ такого способа выведения показывает, что с энергетической точки зрения оптимальным является выведение спутника по полуэллиптической переходной орбите, перигей которой находится на возможно меньшей высоте, а апогей совпадает с перигеем заданной орбиты (рис. 27).
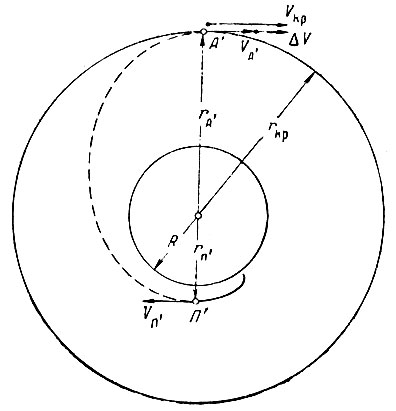
Рис. 27. Схема выведения спутника на круговую орбиту по полуэллиптической переходной орбите: R - радиус Земли; rкр - радиус заданной круговой орбиты; A′ - перигей переходной орбиты; А′ -апогей переходной орбиты; VП′ - скорость в перигее переходной орбиты; VА` - скорость в апогее переходной орбиты; ΔV - дополнительная скорость, которую необходимо сообщить космическому аппарату для перехода на круговую орбиту; Vкр - круговая скорость для заданной орбиты
Угол наклона вектора скорости в конце участка выведения на переходную орбиту, в точке П′, равен нулю ( 0 = 0). Вторичное включение двигателя ракеты производится в точке А′. Направление тяги должно совпадать с касательной к траектории в этой точке.
0 = 0). Вторичное включение двигателя ракеты производится в точке А′. Направление тяги должно совпадать с касательной к траектории в этой точке.
В табл. 19 приведены расчетные значения скорости, которая должна быть сообщена спутнику при выведении его указанным способом на круговые орбиты различной высоты hкр. При расчетах принималось, что высота перигея переходной орбиты составляет 200 км.
| Высота заданной круговой орбиты, км | Скорость в конце участка выведения на переходный эллипс VП′ м/сек | Дополнительная скорость для перехода на заданную орбиту ΔV, м/сек | Суммарная скорость, VΣ, V м/сек |
|---|---|---|---|
| 1000 | 8009 | 214 | 8224 |
| 5000 | 8769 | 854 | 9623 |
| 25000 | 10016 | 1467 | 11483 |
| 50000 | 10424 | 1444 | 11868 |
| 75000 | 10595 | 1358 | 11953 |
| 100000 | 10690 | 1276 | 11966 |
| 125000 | 10749 | 1204 | 11953 |
| 150000 | 10790 | 1143 | 11933 |
| 200000 | 10844 | 1045 | 11889 |
| 11015 | 0 | 11015 |
Из данных, приведенных в таблице, следует, что суммарная скорость, требуемая для выведения спутника, с увеличением высоты заданной орбиты сначала возрастает, а затем несколько падает, стремясь в пределе (при hкр = ∞) к параболической скорости. Максимальное значение суммарной скорости имеет место при высоте круговой орбиты, равной примерно 100 тыс. км. Для этого случая суммарная скорость на 8,5% превышает параболическую скорость на высоте, соответствующей перигею переходной орбиты (200 км). Здесь мы сталкиваемся с парадоксальным явлением, когда запуск спутника на большую высоту требует меньшей суммарной скорости.
При запуске космического аппарата в восточном направлении скорость, приданная ему ракетой, складывается со скоростью поверхности Земли в ее суточном движении.
Увеличение скорости за счет вращения Земли зависит от наклонения орбиты и может быть приближенно выражено формулой:
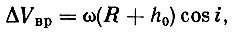 (1.44)
(1.44)где:
R - радиус Земли;
h0- высота точки выведения;
ω - угловая скорость вращения Земли вокруг своей оси;
i - наклонение орбиты.
С уменьшением наклонения орбиты ΔVвр возрастает, достигая для экваториальной орбиты примерно 460 м/сек. Для полярных орбит ∞Vвр равно нулю, а для орбит с наклонением 65°, соответствующих орбитам первых советских спутников, составляет около 200 м/сек.
Ракеты с двигателями, работающими на жидком химическом топливе, в настоящее время получили значительное развитие и достигли высокой степени совершенства.
Наряду с этим развитие ядерной техники позволяет рассматривать вопрос о возможности создания в относительно недалеком будущем космических ракет с двигателями, работающими на ядерной энергии. В таких двигателях тепловая энергия, выделяемая в ядерном реакторе того или иного типа, используется для нагрева некоторой рабочей жидкости (водорода, аммиака, воды) с превращением ее в газ высокой температуры, который истекает из сопла, создавая реактивную тягу.
Основным преимуществом двигателей такого типа по сравнению с двигателями на химическом топливе является возможность получения более высоких значений скорости истечения реактивной струи (удельной тяги), поскольку энергия, сообщаемая рабочей жидкости в реакторе, может значительно превышать энергию, выделяемую при сгорании самых высокоэффективных химических топлив.
Практически значения скорости истечения таких двигателей будут ограничиваться максимальной температурой, выдерживаемой материалами реактора и сопла.
При этом следует иметь в виду, что путем подбора рабочей жидкости может быть получена большая скорость истечения, чем у двигателей на химическом топливе, при одинаковой температуре в камере двигателя. У двигателей, работающих на ядерной энергии, принципиально имеются большие возможности получения высокой скорости истечения реактивной струи, чем у двигателей на химическом топливе.
С точки зрения характеристик движения (протяженности активного участка, ускорения при разгоне) ракеты с двигателями описанного типа не будут существенно отличаться от ракет на химическом топливе.
Особым классом космических ракет явятся космические аппараты с так называемыми электрореактивными двигателями. Одна из разновидностей их - это ионные двигатели, в которых реактивная сила создается за счет отброса потока ионов, разгоняемых при помощи электростатического поля до очень больших скоростей. В качестве рабочего тела, из которого должен образовываться поток ионизированного газа, предполагается использовать элементы, легко поддающиеся ионизации, например, цезий или натрий. Энергия, необходимая для разгона ионизированного газа, может быть получена от ядерной энергетической установки - своего рода атомной электростанции, размещенной в космическом аппарате.
Принципиальная схема ионного двигателя показана на рис. 28. Рабочее тело размещается в баке 2, откуда оно подается соответствующей системой к двигателю. Поступающее в двигатель рабочее тело после нагрева до высокой температуры и прохождения через пористую стенку 3 превращается в ионизированный газ, который затем разгоняется в электростатическом поле, создаваемом системой сеток. 4. Чтобы избежать образования пространственного заряда, препятствующего дальнейшему истечению, ионный поток после разгона должен быть нейтрализован. Для этой цели служит эмиттер электронов 5. Питание двигателя осуществляется от ядерной энергетической установки 6 через преобразователь 7.
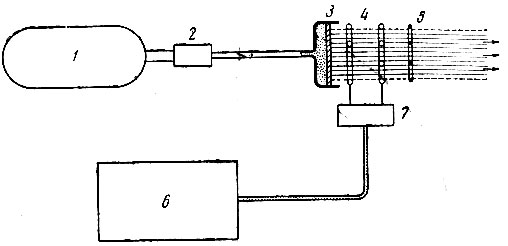
Рис. 28. Схема ионного двигателя: 1 - емкость с запасом рабочего тела (цезия); 2 - система подачи рабочего тела; 3 - пористая стенка; 4 - система сеток, создающих электростатическое поле; 5 - эмиттер электронов; 6 - ядерная энергетическая установка; 7 - преобразователь
Принципиальной особенностью аппаратов с электрореактивными двигателями, резко отличающей их от ракет других типов, является чрезвычайно высокая скорость истечения реактивной струи (до 100-200 км/сек) и весьма малая величина силы тяги и ускорения на активном участке (порядка 10-3 м/сек2).
Невозможность получить большие значения тяги электрореактивных двигателей объясняется тем, что при высокой скорости истечения мощность, необходимая для создания реактивной струи большой тяги, оказывается чрезмерно большой. Так, для получения тяги 1 m при скорости истечения 100 км/сек необходима мощность около миллиона киловатт.
Поэтому если ракеты на химическом топливе, имеющие тягу двигателя больше начального веса, способны самостоятельно взлетать с поверхности Земли и других планет, то космические аппараты с электрореактивными двигателями принципиально лишены такой возможности. Они должны начинать свой полет с орбит искусственных спутников Земли или планет. При этом траектория их движения вначале представляет медленно развертывающуюся спираль (рис. 29). Продолжительность работы двигателей у таких аппаратов, в связи с медленным набором скорости, будет исчисляться многими неделями.
Рис. 29. Схема разгона космического аппарата с ионным двигателем
Основным преимуществом космических аппаратов с электрореактивными двигателями является более благоприятное отношение веса полезного груза к начальному весу аппарата по сравнению с космическими ракетами других типов. Поэтому имеются все основания считать, что в будущем аппараты этого типа станут основным средством, обеспечивающим перелеты между орбитами искусственных спутников планет.
Проблема спуска на поверхность Земли и планет
Осуществление спуска космического аппарата на поверхность Земли и планет является одной из сложнейших проблем, связанных с межпланетными полетами. Движение любого космического аппарата относительно Земли или другого небесного тела происходит со скоростью, равной или большей первой космической скорости. При спуске эта относительная скорость должна быть тем или иным способом снижена до нуля в момент посадки. В настоящее время практически осуществимы два принципиально отличных способа торможения космических аппаратов при спуске. Первый из них основан на использовании реактивной силы, второй - на использовании аэродинамических сил, возникающих при движении космического аппарата в атмосфере.
Для реализации первого способа спуска космический аппарат (или его спускаемая часть) должен быть снабжен двигательной установкой и запасом топлива, обеспечивающими торможение аппарата.
Характеристическая скорость его при этом должна равняться сумме скорости движения относительно поверхности планеты в начале спуска и приращения скорости, вызванного влиянием силы тяготения на участке спуска:
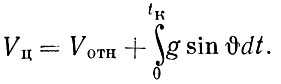 (1.45)
(1.45)Примерные значения характеристической скорости при использовании двигателей на химическом топливе для спуска на поверхность Земли, Луны и некоторых планет даны в табл. 20. В этой же таблице приведены отношения веса полезного груза к начальному весу аппарата (в предположении, что он имеет оптимальное число ступеней, относительный вес конструкции α = 0,1 и скорость истечения реактивной струи с = 4000 м/сек). При этом рассмотрены два случая: спуск с параболической орбиты и спуск с круговой орбиты, расположенной на высоте 1000 км над поверхностью планеты.
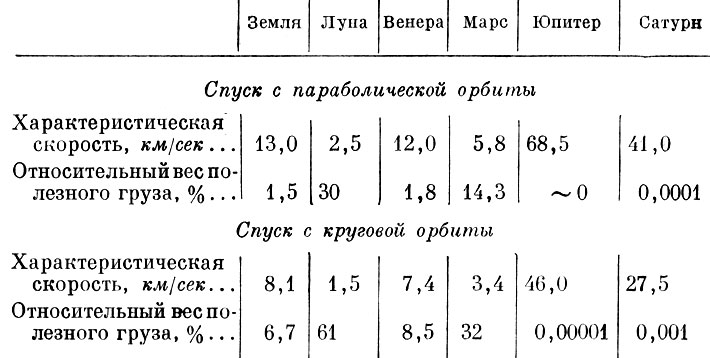
Таблица 20. Характеристическая скорость и относительный вес полезного груза при спуске с использованием реактивной силы
Из таблицы видно, что при использовании наиболее эффективных химических топлив относительный вес полезного груза может составлять: при спуске на Луну - до 30-60%, на Марс - до 15-30%, на Землю и Венеру - менее 10%. При спуске на Юпитер и Сатурн вес полезного груза практически равен нулю. Такой результат вполне естествен, поскольку задача торможения аппарата, движущегося с космической скоростью, с энергетической точки зрения равноценна задаче придания ему такой же скорости.
Однако, несмотря на указанный недостаток описанного способа спуска, он является единственно возможным при посадке на небесные тела, лишенные достаточно плотной атмосферы, и, в частности, при посадке на Луну.
При наличии атмосферы у небесного тела может быть использован второй способ спуска - торможение космического аппарата аэродинамическими силами. Как будет показано ниже, осуществление такого спуска наиболее благоприятно при условии, что космический аппарат предварительно превращен в искусственный спутник, движущийся по достаточно низкой орбите, близкой к круговой.
При спуске с аэродинамическим торможением следует рассмотреть два основных случая:
а) на космический аппарат практически действует только сила сопротивления, и движение его в связи с этим происходит по баллистической траектории;
б) на космический аппарат, помимо силы сопротивления, действует подъемная аэродинамическая сила и он движется по траектории планирования.
В первом случае космический аппарат, или его спускаемая часть, может представлять осесимметричное тело, движущееся с нулевым углом атаки. Во втором - он должен иметь несущие поверхности.
Рассмотрим сначала первый, простейший, случай. Сила сопротивления, действующая на тело, движущееся в атмосфере с большой скоростью, определяется формулой:
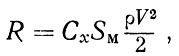 (1.46)
(1.46)где: Сх- коэффициент сопротивления;
SM - площадь миделя аппарата;
ρ - плотность атмосферы на данной высоте;
V - скорость движения аппарата.
Соответственно, перегрузка равняется
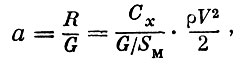 (1.47)
(1.47)где G/SM - нагрузка на мидель.
Величина силы сопротивления, действующей на космический аппарат диаметром 1 ж, в зависимости от высоты и скорости его движения приведена в табл. 21.
Таблица 21. Сила сопротивления в зависимости от высоты и скорости движения, m
Как видно из приведенных данных, сила сопротивления, а следовательно и перегрузка, действующая на космический аппарат, может достигать весьма больших значений, если движение аппарата со скоростью, близкой к космической, происходит на малых высотах. Следовательно, движение космического аппарата в атмосфере должно происходить по такой траектории, на которой обеспечивается постепенное снижение скорости его движения по мере уменьшения высоты.
Такому требованию удовлетворяют траектории, получающиеся при малых отрицательных углах наклона вектора скорости к горизонту при входе в плотные слои атмосферы, на высотах 80-100 км. В табл. 22 приведены расчетные данные, характеризующие возрастание величины максимальной перегрузки, действующей на космический аппарат, в зависимости от увеличения угла входа в плотные слои атмосферы  вх.
вх.
Как видно из таблицы, увеличение угла входа в плотные слои атмосферы с нуля до 5° приводит к возрастанию максимального значения перегрузки вдвое, а до 10° - примерно в четыре раза. При пологих траекториях спуска максимальное значение перегрузки составляет около 8-10. Расчеты показывают, что величина перегрузки мало зависит от нагрузки на мидель и коэффициента сопротивления космического аппарата. В то же время значения этих параметров влияют на скорость аппарата в конце участка спуска, перед его приземлением. Величина этой скорости при спуске по пологим траекториям близка к скорости свободного падения аппарата в атмосфере и составляет несколько сот метров в секунду. Одновременно с воздействием на космический аппарат аэродинамических сил имеет место его интенсивный аэродинамический нагрев. Кинетическая энергия, которой обладал аппарат при входе в атмосферу, превращается в тепловую, вызывая повышение теплосодержания и температуры потока воздуха, омывающего космический аппарат. Представление о величине этой энергии можно получить из следующих цифр. Кинетическая энергия, приходящаяся на 1 кг веса искусственного спутника, движущегося на высоте нескольких сот километров, соответствует тепловой энергии примерно 2,8⋅105 ккал/кг. Если предположить, что все это тепло передается космическому аппарату, то его с избытком хватит, чтобы полностью разрушить аппарат при любой его конструкции. Поэтому основная задача при осуществлении аэродинамического торможения космического аппарата заключается в рассеянии возможно большей части тепловой энергии в окружающую атмосферу с тем, чтобы сам аппарат поглощал минимальную часть выделяемого тепла. Картина аэродинамического нагрева космического аппарата в атмосфере может быть представлена следующим образом (рис. 30). Перед движущимся аппаратом происходит сжатие газа - возникает так называемый скачок уплотнения. Параметры газа за скачком резко изменяются - повышается его температура и давление, происходит сложный комплекс физико-химических превращений газа (диссоциация, ионизация и др.). Кроме того, повышение температуры газа происходит в так называемом пограничном слое, в котором имеет место торможение набегающего потока относительно поверхности аппарата. От нагретого газа, омывающего аппарат, к его поверхности передается значительное количество тепла. Остальная часть выделяемого тепла уносится нагретым газом и рассеивается в атмосфере.
Угол входа траектории в плотные слои атмосферы,  вх вх |
Отношение перегрузки к перегрузке на траектории, соответствующей  вх = 0 вх = 0 |
|---|---|
| 0 | 1,0 |
| 2,5° | 1,2 |
| 5,0° | 1,85 |
| 7,5° | 2,9 |
| 10° | 4,0 |
Наибольший тепловой поток поступает к поверхности аппарата вблизи так называемой критической точки K, в которой имеет место полное торможение набегающего потока. Величина тепловых потоков, поступающих к различным участкам поверхности аппарата, зависит от параметров его движения и формы. Тепло, передаваемое космическому аппарату, частично излучается с его поверхности, а частично идет на нагревание его оболочки и передается внутрь. Температура поверхности аппарата при этом может достигать значений, при которых разрушаются наиболее тугоплавкие материалы. В случае, если она превышает температуру плавления материала оболочки, происходит оплавление, или испарение и унос набегающим потоком материала с поверхности аппарата. Тогда часть тепла поглощается процессами плавления и испарения.
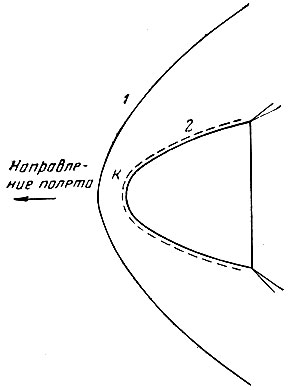
Рис. 30. Схема движения космического аппарата в атмосфере: 1 - скачок уплотнения; 2 - пограничный слой; К - критическая точка
Очевидно, что внешняя оболочка космического аппарата, предназначенного для спуска, во избежание его разрушения должна быть выполнена из материала, обладающего максимально возможной температурой разрушения и требующего максимального количества тепла для плавления или испарения. Вместе с тем в конструкции должны быть предусмотрены меры тепловой защиты, препятствующие передаче тепла внутрь космического аппарата, к его оборудованию и экипажу, с тем, чтобы температура внутри аппарата оставалась в допустимых пределах.
Значения тепловых потоков и температуры поверхности, а также общее количество тепла, поступающего к аппарату на участке спуска, зависят от характера его траектории, определяемой значением  вх, и от нагрузки на мидель G/SM.
вх, и от нагрузки на мидель G/SM.
Минимальная интенсивность тепловых потоков и меньшие значения температур имеют место при наиболее пологих траекториях, т. е. при  вх = 0. С увеличением угла входа в атмосферу интенсивность тепловых потоков и значения температур значительно возрастают.
вх = 0. С увеличением угла входа в атмосферу интенсивность тепловых потоков и значения температур значительно возрастают.
В случаях, когда космический аппарат не имеет каких-либо специальных устройств, существенно увеличивающих его сопротивление (при нагрузке на мидель порядка нескольких сот кг/м2), максимальная температура на его поверхности может превышать температуру разрушения (плавления или испарения) известных в настоящее время материалов, а интенсивность тепловых потоков может достигать десятков тысяч ккал/м2⋅сек.
Сильный нагрев аппарата объясняется тем обстоятельством, что в рассматриваемом случае торможение аппарата происходит в основном на относительно малых высотах (40-50 км), где плотность атмосферы уже достаточно велика.
Представим теперь, что космический аппарат снабжен специальными устройствами, существенно (в несколько десятков или сот раз) увеличивающими его мидель, а следовательно и сопротивление.
Такие устройства можно себе представить, например, в виде парашютов из специальных термостойких материалов, принудительно раскрывающихся перед спуском космического аппарата.
В этом случае интенсивное торможение аппарата начинается на больших высотах (70-80 км), и к моменту снижения скорость его значительно уменьшается. В результате интенсивность тепловых потоков и максимальные значения температур оказываются значительно меньшими, чем в предыдущем случае. Следует, однако, отметить, что создание больших тормозящих устройств из термостойких материалов представляется чрезвычайно сложной технической задачей.
Рассмотрим теперь второй вариант спуска космического аппарата - с использованием несущих поверхностей для создания подъемных сил - так называемый планирующий спуск. Подъемная сила позволяет в этом случае обеспечить поддержание малого угла между траекторией аппарата и местным горизонтом, т. е. сделать траекторию спуска очень пологой. Вследствие этого торможение аппарата происходит в основном на больших высотах, в разреженных слоях атмосферы, и в течение большого времени. Поэтому интенсивность тепловых потоков, максимальные значения температуры поверхности и перегрузки планирующего аппарата оказываются значительно меньшими, чем у аппарата, осуществляющего спуск по баллистической траектории. Для планирующих аппаратов оказывается возможным создать из существующих материалов конструкцию, не подвергающуюся оплавлению. Кроме того, за счет изменения подъемной силы можно в известных пределах управлять траекторией спуска, обеспечивая приземления в заранее выбранном районе.
Таковы основные преимущества планирующего спуска, позволяющие считать, что в будущем планирующие аппараты явятся основным средством спуска на поверхность Земли и других планет.
Необходимо, однако, отметить большие технические трудности, стоящие на пути реализации такого способа спуска. Планирующий аппарат должен обладать аэродинамической формой, обеспечивающей его устойчивость я управляемость в чрезвычайно широком диапазоне скоростей - от дозвуковых до гиперзвуковых. Конструкция его должна сохранять работоспособность при нагреве внешней обшивки до температур, близких к 1500-2000°С. Управление аппаратом должно осуществляться специальной автоматической системой. Для осуществления планирующей посадки с приемлемыми значениями посадочной скорости потребуется введение дополнительных, раскрывающихся перед посадкой, несущих поверхностей.
Сопоставление двух рассмотренных выше способов спуска показывает, что отношение веса полезного груза к общему начальному весу космического аппарата при спуске с использованием аэродинамических сил оказывается значительно более благоприятным, чем при спуске с использованием реактивных сил. Вес средств тепловой защиты, несущих поверхностей и прочих элементов аппарата, тормозящегося аэродинамическими силами, оказывается меньше веса топлива, необходимого для торможения аппарата реактивным двигателем.
В заключение опишем процесс спуска с орбиты искусственного спутника (рис. 31). Представим себе, что спуск осуществляется с круговой орбиты, расположенной на высоте нескольких сот километров над поверхностью Земли. Для перехода космического аппарата, или его спускаемой части, на траекторию спуска необходимо сообщить ему некоторую скорость ΔV в направлении, противоположном его движению по орбите. При ΔV, равной 200-300 м/сек, будет обеспечен угол входа траектории в плотные слои атмосферы порядка нескольких градусов. Движение в атмосфере будет происходить пи баллистической траектории 2 или по траектории планирования 3. В результате аэродинамического торможения скорость аппарата снижается до нескольких сот метров в секунду. После этого должна быть обеспечена посадка аппарата, для чего скорость его должна быть уменьшена до величины, при которой удар о Землю или воду безопасен для конструкции аппарата и его экипажа. Для этой цели, помимо планирующей посадки, может быть применено приземление на парашютах или с помощью тормозных реактивных двигателей.
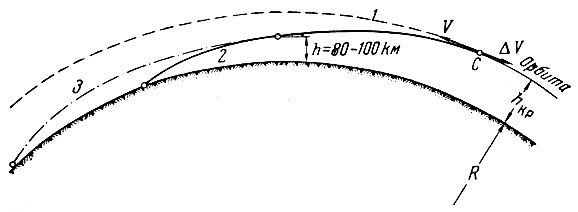
Рис. 31. Траектория спуска космического аппарата с круговой орбиты: R - радиус Земли; hкр - высота круговой орбиты; С - точка перехода на траекторию спуска; ΔV - скорость, сообщаемая космическому аппарату для перехода на траекторию спуска; 1 - участок траектории спуска, лежащий вне плотных слоев атмосферы; 2 - атмосферный участок траектории при баллистическом спуске; 3 - атмосферный участок траектории при планирующем спуске
Устройство космических аппаратов. Основные проблемы, связанные с длительным пребыванием их в космическом пространстве
Тепловой режим космическим аппаратов
Для обеспечения нормальной работы бортовой аппаратуры и возможности пребывания на космических аппаратах живых существ на них должен поддерживаться вполне определенный и достаточно стабильный температурный режим. В связи с этим особое внимание при создании космических аппаратов должно быть обращено на изучение вопросов их теплового режима и разработку мероприятий, позволяющих осуществлять его регулирование.
В тепловом отношении космический аппарат по существу является самостоятельным небесным телом, находящимся в лучистом теплообмене с окружающим пространством. Главным источником лучистой энергии, поступающей к нему извне, является Солнце. Излучение Солнца приближенно соответствует излучению черного тела, имеющего температуру около 6000° К. Поток солнечной энергии характеризуется значением так называемой солнечной постоянной S0 - количеством тепла, поступающего в единицу времени на поверхность, равную 1 м2 и перпендикулярную направлению солнечных лучей. За пределами атмосферы солнечная постоянная равна 1200 ккал/м2час.
Спектральное распределение энергии солнечного излучения представлено на рис. 32. Как видно из этого рисунка, максимум энергии излучения Солнца лежит в видимой области спектра - при длине волн 0,45-0,60 μ.
Рис. 32. Спектральное распределение энергии солнечного излучения
Количество тепла, поступающего к космическому аппарату от Солнца, зависит от площади миделя и степени черноты поверхности аппарата в области максимума энергии солнечного излучения. Последняя величина определяется коэффициентом поглощения солнечной радиации As.
Искусственные спутники нагреваются Солнцем, когда они находятся над освещенной стороной Земли. Для спутников с небольшой высотой орбиты продолжительность этих периодов в большинстве случаев составляет 65-70% от периода обращения по орбите. Однако в некоторых случаях орбита может занимать такое положение, при котором искусственный спутник в течение нескольких суток непрерывно освещается Солнцем (рис. 33).
Рис. 33. Положение орбиты, при котором искусственный спутник непрерывно освещен Солнцем
Вторым основным источником лучистой энергии, поступающей к спутнику, является Земля. Земля отражает часть солнечных лучей, что увеличивает общее количество лучистой энергии Солнца, падающей на спутник. С другой стороны, Земля обладает собственным излучением, воздействующим на спутник как на освещенной, так и на теневой ее сторонах.
Энергия солнечных лучей, отраженных Землей, характеризуется альбедо Земли, значение которого составляет примерно 0,4. Поток лучистой энергии, падающий на спутник за счет отражения Землей солнечных лучей, зависит от положения орбиты по отношению к освещенной части поверхности Земли и от положения спутника на орбите. Он может достигать 35-40% от S0.
Собственное излучение Земли лежит в инфракрасной области, соответствующей длинам волн около 10 μ. Энергия его характеризуется величинами порядка 15% от S0.
Некоторое выделение тепла имеет место при движении спутника в верхних слоях атмосферы в результате соударения молекул воздуха с его поверхностью и возможной рекомбинации атомарного кислорода на ней. Однако выделение этого тепла резко падает с увеличением высоты полета спутника и на высоте 300 км составляет менее 1 % от других внешних потоков тепловой энергии, воздействующих на спутник.
Помимо указанных факторов, на тепловой режим космических аппаратов оказывают существенное влияние и внутренние источники тепловой энергии, основным из которых является их аппаратура. Большая часть энергии, потребляемой аппаратурой при ее работе, преобразуется в конечном счете в тепло, выделяемое внутри космического аппарата. Количество выделяемого тепла зависит от мощности аппаратуры и режима ее включения по времени. Наряду с поглощением тепла космическим аппаратом, происходит теплоотдача с внешней его поверхности за счет излучения в окружающее пространство. Собственное излучение его, как и всякого тела, обладающего сравнительно низкой температурой, лежит в инфракрасной области спектра (длина волн около 10 μ). Количество излучаемого тепла определяется величиной поверхности аппарата, а также ее излучательной способностью, характеризуемой коэффициентом собственного излучения в инфракрасной области спектра ε.
Проанализируем тепловой режим искусственного спутника, находящегося в космическом пространстве, под воздействием перечисленных факторов. При этом, для наиболее ясного представления основных особенностей теплового режима, в первую очередь рассмотрим два предельных случая:
а) собственная теплоемкость спутника (или той его части, тепловой режим которой рассматривается) настолько мала, что практически может быть приравнена к нулю;
б) собственная теплоемкость спутника настолько велика, что колебания его температуры за счет переменности внешних тепловых воздействий пренебрежимо малы.
Кроме того, будем считать, что ориентация орбиты спутника по отношению к Солнцу и освещенной стороне Земли не меняется, внутреннее тепловыделение на спутнике постоянно по времени, а высота орбиты достаточно велика, чтобы пренебречь влиянием физических процессов в верхних слоях атмосферы.
Рассмотрение указанных случаев представляет интерес потому, что в каждом из них мы имеем дело со стационарным тепловым режимом, при котором спутник (или рассматриваемая его часть) принимает некоторую равновесную температуру, определяемую равенством приходящего к спутнику и отдаваемого им тепла. В первом случае спутник в каждый данный момент имеет некоторое текущее значение равновесной температуры, непрерывно изменяющееся при движении спутника по орбите в соответствии с изменением поступающих к нему тепловых потоков. Во втором случае спутник приобретает некоторое постоянное значение равновесной температуры, определяемое средне интегральными значениями тепловых потоков за весь оборот спутника но орбите.
Следует заметить, что рассмотрение указанных случаев представляет не только теоретический, но и практический интерес. Так, если спутник обладает тонкой внешней оболочкой, то температура ее может быть весьма близ-ка к равновесной для каждого момента времени. Соответственно, определение средней равновесной температуры позволяет установить среднее значение температуры, по отношению к которому имеют место ее колебания при движении спутника по орбите.
Значение равновесной температуры легко может быть найдено из уравнения теплового баланса, если исходить из равенства поглощаемого и излучаемого спутником тепла в единицу времени:
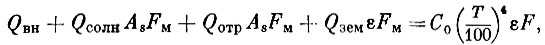 (1.48)
(1.48)где:
Qвн - внутреннее тепловыделение на спутнике;
QсолнAsFм - количество тепла, поглощаемого спутником за счет прямой солнечной радиации;
QотрAsFм - количество тепла, поглощаемого спутником за счет солнечной радиации, отраженной от Земли;
QземεFм - количество тепла, поглощаемого спутником за счет собственного излучения Земли;
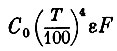
- количество тепла, излучаемого спутником;
Fм - площадь миделя спутника;
F - площадь его поверхности;
C0 - коэффициент лучеиспускания абсолютно черного тела;
Т - температура спутника (по Кельвину);
Аs- коэффициент поглощения солнечной радиации;
ε - коэффициент собственного излучения.
В первом из рассматриваемых случаев значения (Qсолн, Qотр и Qзем соответствуют своим текущим значениям. Во втором случае, как указано выше, эти величины соответствуют своим средне интегральным значениям для данной орбиты.
Значения текущей равновесной температуры (первый случай) при нахождении спутника на освещенной стороне Земли и различной величине коэффициентов As и ε приведены на графике рис. 34. На теневой стороне Земли равновесная температура, независимо от значений этих коэффициентов, составляет около -100° С. На рис. 35 и 36 даны графики средних температур (второй случай) в зависимости от значений As и ε для спутника, движущегося по орбите, плоскость которой совпадает с направлением на Солнце.
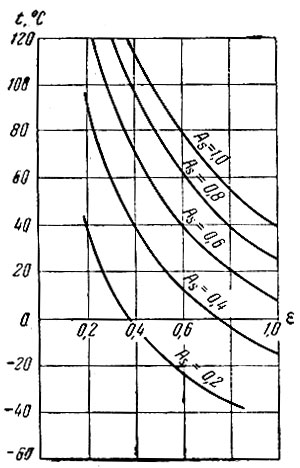
Рис. 34. Текущая равновесная температура оболочки спутника при нахождении его на освещении стороне Земли
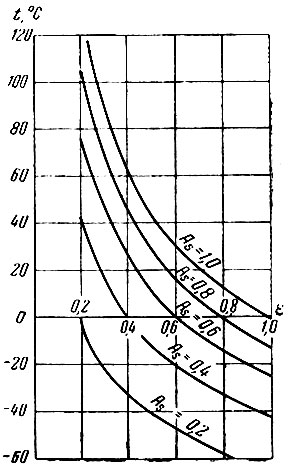
Рис. 35. Средняя температура оболочки спутника при отсутствии внутреннего тепловыделения
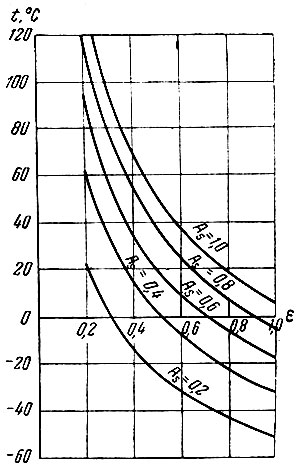
Рис. 36. Средняя температура оболочки спутника при внутреннем тепловыделении
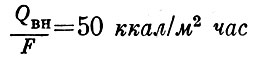
Из рассмотрения приведенных данных видно, что температура спутника может принимать самые различные значения в зависимости от коэффициентов Аs и ε, характеризующих способность поглощения и излучения поверхности спутника в видимой и инфракрасной областях спектра.
Таким образом, первым и обязательным условием для обеспечения на спутнике необходимого теплового режима является придание его поверхности соответствующих значений As и ε. При этом теплоотдача спутника за счет излучения должна компенсировать теплоподвод за счет внешних и внутренних источников тепла. При увеличении внутреннего тепловыделения на спутнике (например, при возрастании мощности аппаратуры) для поддержания неизменного температурного режима должна быть соответственно увеличена излучающая способность оболочки спутника, т. е. коэффициент ε.
Из рис. 35 и 36, в частности, можно установить, что при отсутствии внутреннего тепловыделения средняя температура оболочки спутника порядка +15° С может быть получена при As = 0,4 и ε = 0,3 или при As = 0,8 и ε=0,6.
При относительном внутреннем тепловыделении 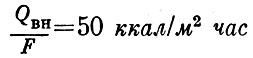 час значения е при тех же As должны быть соответственно увеличены до 0,4 и 0,7.
час значения е при тех же As должны быть соответственно увеличены до 0,4 и 0,7.
Для получения необходимых значений коэффициентов поглощения солнечной радиации и собственного излучения внешнюю поверхность космических аппаратов подвергают специальной обработке.
Соответствующей обработкой поверхности можно добиться, чтобы среднее значение температуры оболочки аппарата было несколько ниже того диапазона температур, который желательно поддерживать в нем. В этом случае отвод тепла, выделяемого внутри аппарата, может быть осуществлен за счет передачи его оболочке.
Наиболее удобно осуществить отвод этого тепла, используя в качестве теплоносителя газ, находящийся внутри герметического отсека космического аппарата. Из-за состояния невесомости, в котором находится космический аппарат при движении по орбите, в нем невозможна свободная конвекция, поэтому заполняющий его газ при отсутствии перемешивания является хорошим теплоизолятором. С другой стороны, создавая принудительную циркуляцию газа внутри аппарата, можно сравнительно легко осуществить передачу значительного количества тепла от его приборов к оболочке.
Регулируя таким образом тепловое сопротивление между внутренними частями космического аппарата и его внешней оболочкой, в зависимости от температуры, можно обеспечить поддержание в нем достаточно стабильного температурного режима.
Для осуществления терморегулирования по указанной схеме необходимо, чтобы основные устройства и аппаратура космического корабля находились в герметическом отсеке, содержащем газ под определенным давлением.
Другим средством воздействия на тепловой режим космического аппарата может явиться непосредственное регулирование количества поглощаемого и отдаваемого им тепла путем изменения соотношения площадей его поверхности, имеющих различные значения коэффициентов As и ε. Для этой цели могут быть применены различные механические устройства (щитки, жалюзи и т.п.). Этот способ регулирования теплового режима был предложен К. Э. Циолковским.
При движении космического аппарата вдали от Земли и других планет их собственное и отраженное излучения на него не действуют. Интенсивность внешнего потока тепла, поступающего к космическому аппарату, определяется в этом случае расстоянием его от Солнца. На расстоянии, соответствующем орбите Марса, величина солнечной постоянной уменьшается примерно в 2,3 раза, на расстоянии, соответствующем орбите Юпитера, - в 27 раз, орбите Сатурна - примерно в 100 раз. На расстоянии, соответствующем орбите Венеры, она возрастает вдвое, а на расстоянии, соответствующем орбите Меркурия, - в 7 раз.
Ориентировочные соотношения коэффициентов As и ε, обеспечивающие поддержание нормальной температуры (+15° С) в космическом аппарате сферической формы в зависимости от удаления его от Солнца (r), приведены на графике рис. 37. Внутреннее тепловыделение при этом принималось равным нулю.
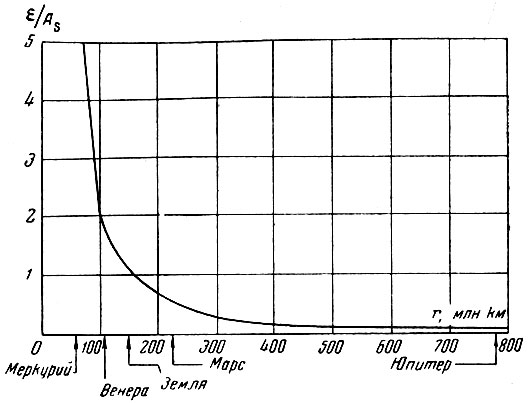
Рис. 37. Соотношения коэффициентов е я. As, обеспечивающие поддержание температуры +15° С в космическом аппарате при различном удалении его от Солнца
В заключение следует отметить, что приведенные выше соображения и расчеты имеют своей целью лишь проиллюстрировать основные закономерности теплового режима космических аппаратов и дать представление о способах управления им. Изучение теплового режима реальных космических аппаратов является весьма сложной технической задачей.
Обычно космические аппараты имеют конструкцию, отдельные элементы которой обладают различной собственной теплоемкостью и находятся в определенном тепловом контакте друг с другом. Вместе с тем тепловые потоки, поступающие извне, и внутреннее тепловыделение, как правило, изменяются по времени в весьма широких пределах. В связи с этим решение указанной задачи связано с проведением детального анализа нестационарных режимов сложных в тепловом отношении систем в условиях резко меняющихся тепловых воздействий.
Герметизация и метеорная опасность
В большинстве случаев космические аппараты должны иметь герметические отсеки, заполненные воздухом или другим газом (азотом, гелием).
В автоматических аппаратах наличие газообразного наполнителя создает благоприятные условия для функционирования их аппаратуры и способствует поддержанию стабильного внутреннего температурного режима. В космических аппаратах, предназначенных для полетов человека или животных, наличие воздуха с давлением, близким к атмосферному, является совершенно обязательным.
В связи с этим при создании космических аппаратов возникает задача обеспечения на весьма длительное время надежной и полной их герметичности (или герметичности их отдельных отсеков) в условиях глубокого внешнего вакуума и периодических изменений температурного режима оболочки.
В ряде случаев решение этой задачи сопряжено со значительными техническими трудностями, тем более, что при создании космического аппарата необходимо обеспечить минимальный вес его конструкции. Особенно важным является обеспечение надежной герметичности для аппарата с людьми, поскольку утечка воздуха из аппарата может оказаться гибельной для его обитателей. Одной из причин, могущих привести к нарушению герметичности космического аппарата и повреждению его оборудования, является возможное повреждение его оболочки метеорами.
В межпланетном пространстве движется большое количество твердых тел самых различных размеров - метеоров. При этом количество метеорных тел в единице объема космического пространства возрастает с уменьшением их размеров. Следовательно, вероятность встречи космического аппарата с малыми метеорными телами неизмеримо больше, чем опасность встречи его с метеорами крупных размеров.
Для оценки метеорной опасности прежде всего необходимо выяснить, какова вероятность встречи космического аппарата с метеорными телами того или иного размера.
К настоящему времени основные данные о количестве метеорного вещества в межпланетном пространстве и о распределении метеоров по массам получены главным образом из наблюдений за метеорами, попадающими в земную атмосферу. На основании обработки многочисленных наблюдений установлено, что количество метеоров того или иного размера в единице объема космического пространства примерно обратно пропорционально квадрату их массы. По имеющимся в литературе оценкам, зависимость числа метеорных частиц от их массы может быть представлена в виде:
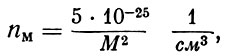 (14.9)
(14.9)где nм- число частиц, имеющих массу М, в единице объема (масса -в граммах).
При этом следует заметить, что данная оценка числа метеорных частиц является максимальной из известных в настоящее время.
Тогда число частиц, имеющих массу, равную или большую М, в единице объема будет равно:
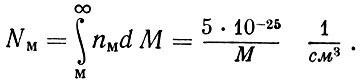 (1.50)
(1.50)Вероятность встречи космического аппарата с метеорами, имеющими массу, равную или большую М, можно оценить следующей формулой:
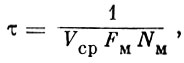 (1.51)
(1.51)где τ - среднее время между двумя встречами с метеорами, имеющими массу, большую или равную М;
Fм-площадь проекции космического аппарата (его средний мидель);
Vcp -средняя скорость метеоров (30-50 км/сек). Результаты расчетов по этой формуле для космического аппарата, имеющего мидель 1 м2, приведены в табл. 23.
| Масса метеорных частиц, г | Среднее время между двумя встречами с метеорами |
|---|---|
| 1⋅10-10 | 1,5 часа |
| 1⋅10-8 | 6 суток |
| 1⋅10-6 | 1,6 года |
| 1⋅10-4 | 160 лет |
Приведенные данные характеризуют вероятность встречи космического аппарата с так называемыми спорадическими (появляющимися случайно, время от времени) метеорами. Помимо спорадических метеоров, орбиту Земли периодически пересекают метеорные потоки, закономерно движущиеся по своим орбитам вокруг Солнца.
При пересечении Землей метеорного потока вероятность попадания метеоров в космический аппарат возрастает. Однако движение метеорных потоков к настоящему времени достаточно хорошо изучено, что позволяет заранее прогнозировать периоды максимумов метеорной интенсивности.
Вторым основным вопросом при оценке метеорной опасности является выяснение пробивной силы метеорных частиц различных размеров. Решение этого вопроса путем постановки прямых экспериментов в земных условиях до настоящего времени не представлялось возможным, ввиду чрезвычайно больших скоростей движения метеорных частиц (до 50-70 км/сек).
Некоторые теоретические исследования вопроса о пробивном действии метеоров позволяют предполагать, что метеоры способны пробивать металлические оболочки, имеющие толщину, равную 8-20 диаметрам метеорных частиц, при условии, что плотность их соответствует плотности каменных или железных метеоритов, достигающих поверхности Земли.
Если исходить из приведенных выше данных, то можно прийти к выводу, что для малых космических аппаратов метеорная опасность невелика. Так, для аппарата, имеющего диаметр 0,5 м и толщину оболочки 1 мм, среднее время между встречами с метеорами, способными пробить его оболочку, составит не менее чем несколько лет. Однако при увеличении размеров аппарата вероятность пробития его оболочки повышается пропорционально возрастанию площади его миделя. Например, для спутника-станции, имеющего площадь миделя в несколько сот квадратных метров, можно ожидать, что пробитие его оболочки будет происходить в среднем раз в несколько недель. Поэтому для больших искусственных спутников и космических кораблей может потребоваться разработка ряда мероприятий по обеспечению их герметичности и защите людей и аппаратуры от метеорных частиц.
В заключение необходимо отметить, что приведенные выше оценки метеорной опасности являются сугубо ориентировочными. Детальное исследование вопросов метеорной опасности и практическое решение проблемы борьбы с ней могут быть осуществлены лишь путем постановки прямых опытов и измерений непосредственно на искусственных спутниках и космических ракетах.
Бортовая аппаратура. Передача информации. Измерение параметров движения
Для проведения научных исследований космические аппараты снабжаются различными видами научной и измерительной аппаратуры, а также рядом дополнительных устройств и систем. К ним относятся:
1. Собственно научная аппаратура - приборы, непосредственно производящие научные измерения или обеспечивающие постановку соответствующих экспериментов в верхних слоях атмосферы и космическом пространстве.
2. Радиотелеметрическая аппаратура, осуществляющая передачу результатов научных измерений на Землю.
3. Радиоаппаратура, позволяющая производить радионаблюдения за космическим аппаратом и измерять параметры его движения.
4. Устройства и аппаратура, обеспечивающие управление всеми бортовыми системами космического аппарата.
5. Устройства для создания условий, необходимых для нормального функционирования бортовой аппаратуры.
6. Источники электропитания бортовой аппаратуры. Вся бортовая аппаратура должна быть рассчитана на работу в условиях невесомости и выдерживать значительные ускорения, имеющие место при выведении космического аппарата на орбиту. Одним из основных требований к этой аппаратуре является ее малый вес и габариты, а также минимальное потребление ею электроэнергии. Вместе с тем она должна отличаться высокой надежностью при длительной работе.
Это обусловливает использование при разработке бортовой аппаратуры космических аппаратов ряда новейших достижений современной науки и техники. В частности, в их аппаратуре находят самое широкое применение различные полупроводниковые приборы, заменяющие собой электронные лампы и некоторые другие радиотехнические элементы. Полупроводниковые приборы обладают рядом существенных преимуществ. Одним из них является их огромный срок службы, достигающий десятков тысяч часов, в то время как обычные радиолампы способны работать не более 500-1000 часов. Другим их преимуществом являются малые габариты и крайне малое потребление энергии. Использование полупроводниковых диодов и триодов в сочетании с современными малогабаритными радиодеталями позволяет создавать чрезвычайно легкую, компактную, надежную и экономичную бортовую аппаратуру.
Состав научной аппаратуры космического аппарата определяется программой проводимых на нем научных исследований.
Обычно каждый из научных приборов состоит из двух основных частей: чувствительного элемента (датчика), непосредственно осуществляющего измерение той или иной физической величины, и усилительно-преобразовательного электронного устройства, усиливающего сигналы датчика и преобразующего их в форму, удобную для передачи на Землю.
Датчики научной аппаратуры весьма разнообразны. Тип каждого из датчиков, его конструкция, а также размещение определяются характером физической величины, для измерения которой он служит.
Некоторые из датчиков должны размещаться вне герметической кабины и иметь непосредственный контакт с окружающим пространством. К ним относятся манометры, осуществляющие измерение давления в верхних слоях атмосферы, фотоумножители аппаратуры для изучения коротковолнового и корпускулярного излучений Солнца, ловушки заряженных частиц, датчики, регистрирующие удары метеорных частиц, и т. д.
Другие датчики - счетчики для измерения космических лучей, магнитометры и т. д.- в большинстве случаев могут быть помещены внутри самого аппарата.
Усилительно-преобразовательные устройства научных приборов также весьма разнообразны по своей схеме и назначению. В простейшем случае - это усилитель, обеспечивающий подачу на вход телеметрической системы напряжения, пропорционального измеряемой величине. В некоторых случаях - это весьма сложные электронные устройства, имеющие в своем составе различные счетные и логические схемы, следящие системы, преобразователи формы импульсов, дискриминаторы, различающие сигналы по их амплитудам, и т. д.
Электронные устройства научных приборов обычно осуществляют также выработку различных переменных напряжений, необходимых для работы датчиков.
Передача результатов научных измерений с космического аппарата на Землю производится с помощью радиотелеметрических систем*. Радиотелеметрические сиcтемы в настоящее время широко применяются при испытаниях самолетов, при высотных запусках ракет с научной аппаратурой и в ряде других случаев, когда бывает необходимо передавать результаты измерений на большие расстояния.
* (Радиотелеметрия - передача по радио данных измерений физических и электрических величин.)
Радиотелеметрическая система включает в себя бортовую аппаратуру, размещаемую на космическом аппарате, а также одну или несколько наземных приемных станций. Бортовая телеметрическая аппаратура осуществляет преобразование измеряемых величин в радиосигналы определенного вида, излучаемые затем радиопередатчиком телеметрической системы. Наземные станции производят прием этих сигналов и преобразуют их в форму, удобную для регистрации.
Существуют различные способы формирования телеметрических сигналов. Один из них заключается в генерировании некоторой частоты (так называемой поднесущей), которой затем модулируется основная, несущая частота радиопередатчика. При этом поднесущая частота изменяется в зависимости от напряжения, поступающего на вход телеметрической системы, т. е. в зависимости от измеряемой величины. Например, поднесущая частота может быть пропорциональна измеряемой величине. Такой способ формирования телеметрических сигналов носит название частотной модуляции (рис. 38, а).
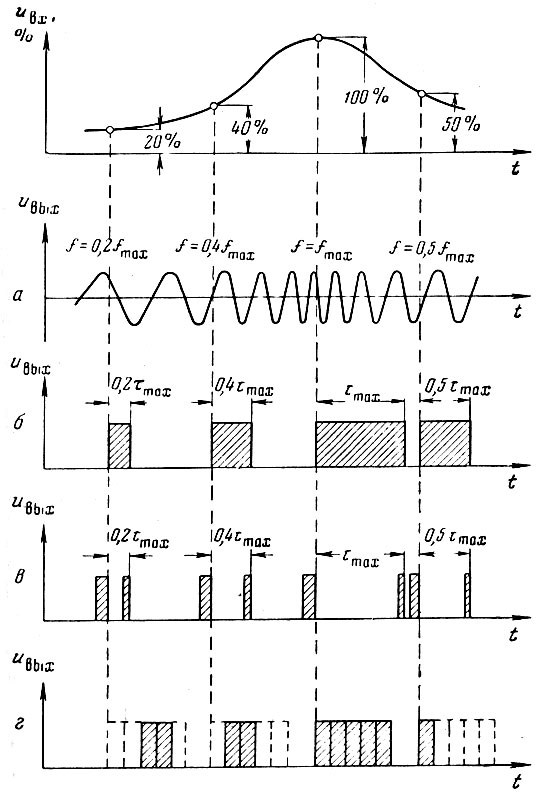
Рис. 38. Схема формирования телеметрических сигналов: а - частотная модуляция; б - широтно-импульсная модуляция; в - время-импульсная модуляция; г - кодово-импульсная модуляция
После приема радиосигналов наземной станцией производится выделение поднесущей частоты и измерение ее. В результате на выходе соответствующего блока наземной станции вырабатывается напряжение, пропорциональное измеряемой величине.
Другой способ формирования телеметрических сигналов, называемый широтно-импульсной модуляцией, заключается в последовательной передаче по радиоканалу импульсов, длительность (ширина) которых пропорциональна измеряемой величине в некоторые моменты времени (см. рис. 38, б). В этом случае измеряемая величина передается не непрерывное отдельными дискретными значениями, которые соответствуют моментам "опроса" телеметрической системой данного прибора. Следует, однако, отметить, что частота опросов в современных радиотелеметрических системах обычно достаточно велика.
Аналогична широтно-импульсной так называемая время-импульсная модуляция, при которой в зависимости от значения измеряемой величины меняется промежуток времени между передачей опорного и измерительного импульсов (см. рис. 38, в).
При широтно-импульсной и время-импульсной модуляциях после приема радиосигналов наземной станцией производится измерение длительности принимаемых импульсов или промежутков времени между ними, в результате чего вырабатывается напряжение, пропорциональное измеряемой величине.
Известны и другие виды формирования телеметрических сигналов, например кодово-импульсная модуляция с двоичным кодом. В этом случае отдельные значения измеряемой величины преобразуются в двоичные числа и передаются в виде групп импульсов, в которых импульсы обозначают единицы, а отсутствие импульсов - нули (см. рис. 38, г).
Современные радиотелеметрические системы обеспечивают одновременную передачу большого числа измеряемых величин. В таких системах, называемых многоканальными, специальным коммутирующим устройством производится поочередное подключение ко входу системы ряда научных приборов и датчиков. Частота подключений (частота "опроса") может составлять от нескольких раз до нескольких сот раз в секунду.
При малых скоростях опроса обычно используются механические коммутаторы. Механический коммутатор представляет собой диск из изоляционного материала, по периферии которого установлен ряд контактов - ламелей. В центре диска имеется ось, на которой с помощью специального электродвигателя вращается щетка, поочередно касающаяся отдельных ламелей. Таким образом, в каждый момент времени с одной из ламелей снимается напряжение, пропорциональное измеряемой величине прибора или датчика, подключенного к ней. Напряжение, снимаемое с ламели, поступает в блок формирования, в котором оно преобразуется в телеметрические сигналы одним из вышеописанных способов.
Наряду с механическими коммутаторами, в телеметрических системах широко используются так называемые электронные коммутаторы, обладающие рядом преимуществ при больших частотах опроса (несколько сот раз в секунду).
В наземных телеметрических станциях также имеются коммутирующие устройства, работающие синхронно с бортовым коммутатором. В результате телеметрические сигналы, передаваемые по одному общему радиоканалу, после их приема и усиления направляются по нескольким измерительным каналам, что создает возможность раздельной регистрации измеряемых величин, которая производится на фотографической бумаге или пленке, подобно тому, как это делается в обычных осциллографах. Синхронизация бортовых и наземных коммутирующих устройств производится специальными синхронизирующими импульсами, также передаваемыми по радиоканалу телеметрической системы.
Форма телеметрических сигналов, передаваемых многоканальной системой при широтно-импульсной модуляции, показана на рис. 39.
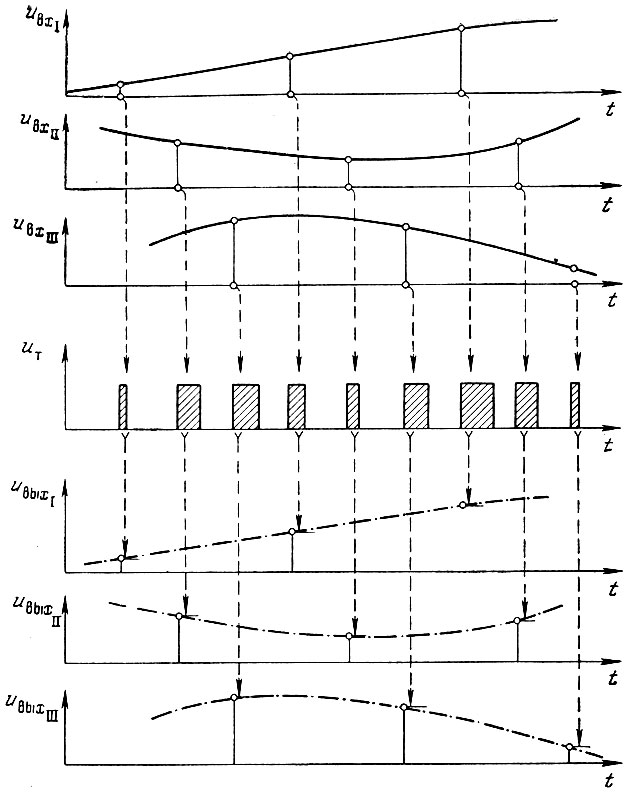
Рис. 39. Форма телеметрических сигналов, передаваемых многоканальной системой при широтно-импульсной модуляции: uвх - передаваемые величины; uвых - регистрируемые величины
На рис. 40 приведена общая схема радиотелеметрической системы.
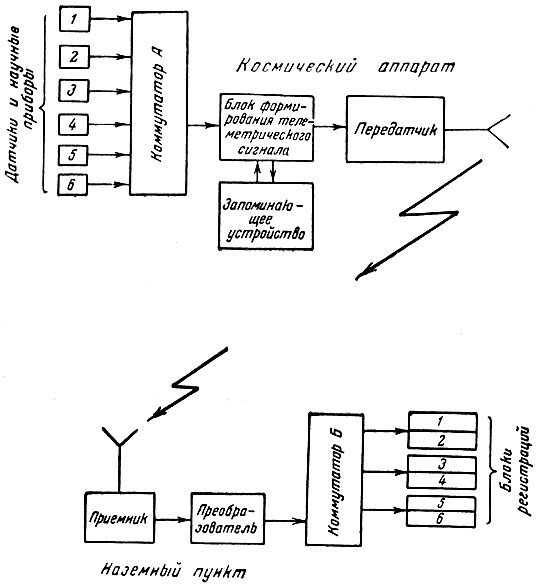
Рис. 40. Схема радиотелеметрической системы
Радиотелеметрические системы, предназначенные для космических аппаратов, отличаются большим временем работы. Телеметрические системы спутников в большинстве случаев должны быть снабжены так называемыми запоминающими устройствами, которые фиксируют результаты измерений в той или иной форме, например, в виде записи на магнитную ленту, в течение всего времени движения спутника по орбите. При очередном пролете спутника над наземными станциями производится передача информации с увеличенной скоростью. Использование в составе телеметрической системы запоминающего устройства позволяет проводить научные измерения непрерывно в течение длительного времени с охватом всех районов земного шара, над которыми пролетает спутник.
Чрезвычайно важной задачей при осуществлении полетов космических аппаратов является измерение характеристик движения космического аппарата (координат и составляющих вектора скорости) в различные моменты времени. На основании этих данных производится определение орбиты космического аппарата и прогнозирование его движения, необходимое для выдачи целеуказаний наземным наблюдательным пунктам.
Измерение координат космического аппарата может осуществляться различными методами, основанными на использовании принципа равносильной зоны, эффекта Допплера, принципов пассивной или активной радиолокации и т.д. Некоторые из этих методов требуют наличия весьма сложного наземного оборудования. Другие относительно просты и в отдельных случаях могут быть реализованы радиолюбителями.
Эффект Допплера заключается в том, что при относительном сближении (или удалении) радиопередатчика и приемника частота сигнала, принимаемого приемником, отличается от частоты сигнала, излучаемого передатчиком, на некоторую величину, пропорциональную скорости сближения (или удаления):
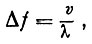 (1.52)
(1.52)где ν - скорость изменения расстояния между передатчиком и приемником;
λ - длина волны, на которой работает радиопередатчик.
При сближении частота принимаемого сигнала больше, а при удалении меньше частоты излучаемого сигнала.
Изложим один из методов определения координат искусственных спутников, основанный на эффекте Допплера. На спутнике устанавливается радиопередатчик, работающий в режиме непрерывного излучения или излучающий достаточно длительные импульсы. Наземные измерительные пункты снабжаются чувствительными приемниками и устройствами для измерения частоты принимаемых сигналов.
Характер движения спутника по отношению к некоторому пункту показан на рис. 41. Вначале, когда спутник удален от наземного пункта (точка A1, скорость изменения расстояния между ними максимальна и практически совпадает со скоростью движения спутника. Затем, по мере приближения спутника, угол между направлением его движения и линией АО (спутник - наземный пункт) увеличивается. В связи с этим скорость сближения начинает падать. В тот момент, когда спутник проходит на кратчайшем расстоянии от наземного пункта (точка А2), скорость их сближения становится равной нулю, поскольку угол между направлением движения спутника и линией АО в этот момент составляет 90°. В дальнейшем происходит удаление спутника от наземного пункта, причем скорость удаления постепенно повышается, приближаясь к скорости движения спутника (точка А3). График скорости изменения расстояния между спутником и наземным пунктом (по времени) для различных удалений наземного пункта от плоскости орбиты р представлен на рис. 42.
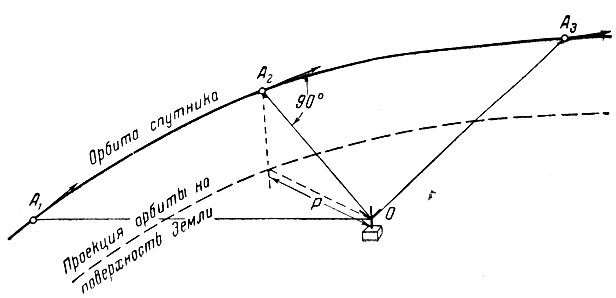
Рис. 41. Схема движения спутника по отношению к наземному пункту: 0 -наземный пункт; р - удаление наземного пункта от плоскости орбиты; А - положение спутника в различные моменты времени
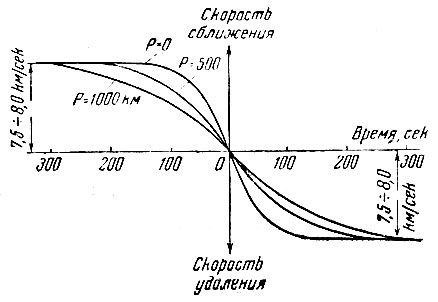
Рис. 42. Скорость изменения расстояния между спутником и наземным пунктом
Из формулы (1.52) видно, что изменение частоты принимаемого сигнала пропорционально скорости изменении расстояния между передатчиком и приемником. Поэтому график изменения частоты принимаемого радиосигнала по времени (рис. 43) по своему характеру совершенно аналогичен графику рис. 42. Чем ближе пролетает спутник по отношению к наземному пункту, тем быстрее изменяется частота принимаемого сигнала от максимального значения до минимального.
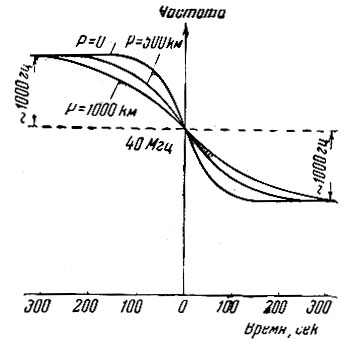
Рис. 43. Изменение частоты принимаемого радиосигнала по времени
Регистрируя частоту принимаемого радиосигнала, можно с достаточно большой точностью установить момент прохождения спутника на минимальном расстоянии от наземного пункта, соответствующий точке А2 на рис. 41. Зная моменты прохождения спутника на минимальном расстоянии по отношению к нескольким наземным пунктам, представляется возможным вычислить основные параметры его орбиты.
Метод равносигнальной зоны основан на использовании для приема радиосигналов спутника двух антенн, расположенных в одном наземном пункте, но имеющих сдвинутые друг относительно друга на некоторый угол а максимумы диаграмм направленности (рис. 44).
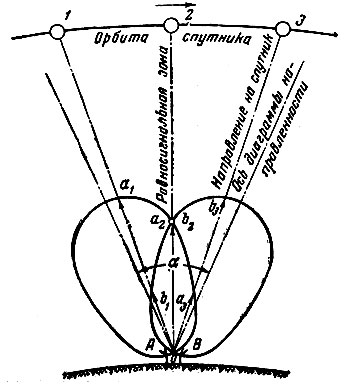
Рис. 44. Схема равносигнальиой зоны, образуемой двумя антеннами: А и В - приемные антенны; а и b - интенсивности принимаемых сигналов в различные моменты времени; α - угол между максимумами диаграмм направленности
При нахождении спутника в точке 1 сигналы, принимаемые антенной А, по интенсивности больше сигналов, принимаемых антенной В (а1 > b1). В момент пролета спутником точки 2 интенсивность сигналов, принимаемых обеими антеннами, одинакова (а2 = b2). В дальнейшем (точка 3) сигналы, принимаемые антенной 5, начинают превышать по интенсивности сигналы, принимаемые антенной А (а3 < b3).
Сравнивая уровни сигналов, принимаемых обеими антеннами, можно определить момент пролета спутника через плоскость, соответствующую направлению оси равносигнальной зоны.
Равносигнальная зона может быть получена и при использовании одной антенны, диаграмма направленности которой периодически меняет свое положение в пространстве (так называемое сканирование - рис. 45). На этом принципе осуществляется измерение угловых координат большинством современных радиолокаторов.
Рис. 45. Схема равносигнальной зоны, образуемой сканированием диаграммы направленности антенны
Простейшая пеленгационная приставка к радиоприемнику для измерения угловых координат спутника методом равносигнальной зоны может быть выполнена квалифицированным радиолюбителем.
К числу радиометодов, пригодных для точного определения угловых координат космических аппаратов, относится и так называемый фазовый метод. Поясним его сущность на простейшем примере (рис. 46). На космическом аппарате устанавливается радиопередатчик, работающий на некоторой частоте λ. Прием его сигналов производится на две приемные антенны, располженные на расстоянии а одна от другой. Это расстояние соответствует п длинам волн (а = nλ) или разности фаз 360 n градусов. Очевидно, что сигналы передатчика будут приходить к антенне A и в точку Р одновременно, а второй антенны В они будут достигать с некоторой задержкой, зависящей от величины отрезка РВ. Величину этого отрезка можно определить, сравнивая фазы сигналов, принятых антеннами А и В. Действительно, пусть разность фаз принимаемых сигналов составляет ср градусов, что соответствует 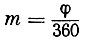 длинам волн, которые укладываются на отрезке РВ. Тогда РВ = λm. В то же время отрезок РВ и базовое расстояние а при условии, что расстояние от передатчика до антенн много больше базы, находится в соотношении РВ = a cos α. Следовательно,
длинам волн, которые укладываются на отрезке РВ. Тогда РВ = λm. В то же время отрезок РВ и базовое расстояние а при условии, что расстояние от передатчика до антенн много больше базы, находится в соотношении РВ = a cos α. Следовательно,
 (1.53)
(1.53)
Рис. 46. Схема фазометрической системы: А и В - приемные антенны; а - база
Таким образом, по разности фаз принимаемых сигналов можно определить косинус угла между направлением на передатчик и базовой линией антенн.
Имея два комплекта антенн, боковые линии которых взаимно перпендикулярны, можно измерить два направляющих косинуса, а следовательно, определить направление на передатчик в пространстве.
Поскольку в фазовых системах для получения высокой точности величина базы выбирается значительно большей, чем длина волны, система имеет неоднозначный отсчет углов. Так, если измеренная разность фаз составляет 35°, то в действительности разность фаз может составлять 35°, 395° или 360n + 35°. Для исключения неоднозначности отсчета в фазовых системах используют дополнительные антенны, установленные на меньших базах.
Описанные методы радиоизмерений позволяют определять угловые координаты космических аппаратов. Наряду с этим во многих случаях для точного определения орбит необходимо измерение дальностей. Особое значение измерение дальностей имеет для космических аппаратов, удаляющихся от Земли на большие расстояния. Объясняется это тем обстоятельством, что при измерении углов линейные погрешности определения координат возрастают пропорционально дальности. Так, при дальности 380 тыс. км (среднее расстояние от Земли до Луны) угловая погрешность, равная одной минуте, соответствует ошибке в определении координат около 100 км. При полетах к Марсу или Венере, когда космические аппараты могут удаляться от Земли на расстояния порядка 200 млн. км и более, той же угловой погрешности соответствуют ошибки в координатах, достигающие десятков тысяч километров. В то же время при измерении радиометодами дальности погрешность измерений мало зависит от самой дальности.
Методы измерения дальности, применяемые в настоящее время в радиолокации, основаны на измерении промежутка времени между посылкой радиосигнала измерительной станцией и приемом ею радиосигнала, отраженного от объекта. Зная этот промежуток времени и скорость распространения радиоволн, можно определить дальность от измерительной станции до объекта по формуле:
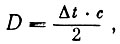 (1.54)
(1.54)где;
Δt - промежуток времени между посылкой и приемом радиосигнала;
с - скорость распространения радиоволн.
Поскольку мощность отраженного сигнала при малых размерах объекта незначительна, на космических аппаратах обычно устанавливаются приемо-передатчики (ответчики), принимающие сигналы наземных измерительных станций и излучающие ответные сигналы достаточно большой мощности.
Помимо передачи телеметрической информации и измерения координат, устанавливаемая на космических аппаратах радиопередающая аппаратура позволяет также изучать распространение радиоволн в верхних слоях атмосферы и ионосфере, что имеет большое научное и практическое значение.
К радиоэлектронной аппаратуре космических аппаратов относятся также телевизионные системы, которые могут применяться для передачи на Землю изображений Луны и других планет.
Такие системы основаны на принципе сравнительно медленной передачи изображения, полученного фотографическим путем, и называются в связи с этим фототелевизионными. Непосредственная передача изображения при большом числе строк разложения и значительном числе кадров в секунду, как это имеет место в обычном телевидении, на большие расстояния (миллионы километров) при современном состоянии радиотехники неосуществима, поскольку она требует очень широкой полосы пропускания радиолинии и соответственно громадных мощностей радиопередающих устройств.
Из вышеизложенного видно, насколько важное значение имеет развитие радиоэлектроники для осуществления космических полетов.
Для радиосвязи с космическими аппаратами могут применяться радиосистемы, работающие на различных частотах (длинах волн). Однако диапазон длин волн, используемых для этой цели, ограничен определенным пределом, обусловленным свойствами земной атмосферы. Для волн длиннее 20-25 м ионосфера практически непрозрачна. Эти волны целиком отражаются и поглощаются ионосферными слоями, обладающими высокой электронной концентрацией.
Выбор рациональных длин волн для радиосвязи с космическими аппаратами определяется многими факторами - назначением радиосистемы, дальностью ее действия, характером передаваемых сигналов и др. Во многих случаях на космических аппаратах устанавливают несколько радиосистем, работающих на различных длинах волн.
Одной из серьезнейших проблем является обеспечение радиосвязи с космическими аппаратами, удаляющимися от Земли на большие расстояния. При полетах к Луне дальность радиосвязи должна составлять 400-500 тыс. км. Полеты к ближайшим планетам - Марсу и Венере - связаны с необходимостью осуществления радиосвязи на сотни миллионов километров, а полеты к Юпитеру и Сатурну - на расстояний порядка тысячи миллионов километров.
Рассмотрим, какими факторами определяется дальность радиосвязи в космическом пространстве.
Обязательным условием, обеспечивающим возможность радиоприема, является превышение мощности принимаемого сигнала над мощностью шумов на входе приемного устройства
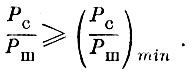
Мощность принимаемого сигнала зависит от мощности передатчика, коэффициента направленности передающей антенны и соотношения эффективной площади приемной антенны к поверхности сферы с радиусом, равным расстоянию от передатчика до приемника:
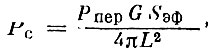 (1.55)
(1.55)где Рпер- мощность передатчика,
G- коэффициент направленности передающей антенны;
Sэф - эффективная площадь приемной антенны;
L - расстояние между передатчиком и приемником.
Шумы в приемном устройстве складываются из шумов космического радиоизлучения и собственных шумов приемника. Мощность их определяется формулой:
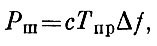 (1.56)
(1.56)где;
с - постоянная Стефана - Больцмана,
Тпр - приведенная температура, характеризующая уровень собственных шумов приемника и интенсивность космического радиоизлучения;
Δf - ширина полосы пропускания приемника. Отношение мощности принимаемого сигнала к мощности шумов равно:
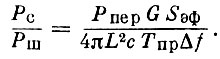
Отсюда можно получить формулу предельной дальности радиосвязи:
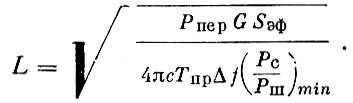 (1.57)
(1.57)Как видно из формулы, основными мероприятиями, позволяющими увеличить дальность связи, помимо повышения мощности передатчика, которая для бортовых устройств обычно ограничена, могут явиться: применение приемных антенн большой эффективной площади; использование передающих антенн высокой направленности; применение специальных средств, обеспечивающих снижение собственных шумов приемника (молекулярных и параметрических усилителей, криостатов и т. п.); сужение полосы пропускания приемника, что связано с уменьшением скорости передачи информации.
При этом увеличение дальности связи сопряжено с большими трудностями, поскольку она изменяется пропорционально корню квадратному от изменения указанных параметров. Однако расчеты показывают, что, используя новейшие достижения радиоэлектроники и создавая наземные антенны достаточно больших размеров, можно будет осуществлять радиосвязь с космическими аппаратами на расстояниях, достигающих сотен и тысяч миллионов километров.
Управление аппаратурой автоматических космических аппаратов, ее периодическое включение и выключение производится специальными устройствами по заданной временной программе. Такие программные устройства, в частности, могут быть осуществлены в виде электронных систем, целиком выполненных на полупроводниках, как это сделано, например, на третьем советском искусственном спутнике Земли. В некоторых случаях управление аппаратурой может производиться по радиокомандам, передаваемым с Земли. Такой способ управления бортовой аппаратурой имеет особое значение при длительном полете космического аппарата, когда предварительное задание определенной программы работы его аппаратуры не представляется возможным.
Из устройств, обеспечивающих создание условий, необходимых для нормального функционирования бортовой аппаратуры, необходимо прежде всего отметить системы терморегулирования. Эти системы должны иметь чувствительные элементы, регистрирующие температуру внутри космического аппарата, и исполнительные органы, воздействующие тем или иным способом на его тепловой режим. Способы регулирования теплового режима были изложены в предыдущем разделе.
На космических аппаратах, предназначенных для размещения подопытных животных, так же как и на космических аппаратах с людьми, помимо системы терморегулирования, обязательным является наличие таких устройств, как система регенерации состава воздуха, система вентиляции и т. п.
В ряде случаев для проведения тех или иных научных исследований необходимо, чтобы космический аппарат был определенным образом ориентирован по отношению к окружающим небесным телам (Земле, Солнцу или звездам).
Так, для изучения процессов, происходящих на Солнце, требуется, чтобы одна из осей аппарата, соответствующая направлению установки чувствительных элементов научной аппаратуры, была в течение длительного времени ориентирована на Солнце.
Определенная ориентация космического аппарата может быть обеспечена соответствующей системой ориентации.
Для иллюстрации принципа работы такой системы на рис. 47 дана схема системы ориентации аппарата на Солнце. Чувствительный элемент системы А, состоящий из нескольких фотоэлементов, измеряет отклонение некоторой оси аппарата х от направления на Солнце. Сигналы с чувствительного элемента, зависящие от величины измеренного отклонения, поступают в усилительно-преобразующее устройство Б у которое вырабатывает необходимые команды, передаваемые на органы управления В. Органы управления поворачивают космический аппарат относительно его центра масс таким образом, чтобы направить ось х на Солнце. Непрерывная работа системы обеспечивает сохранение заданной ориентации аппарата.
Такая система обеспечивает одноосную ориентацию космического аппарата. Для полной (трехосной) ориентации аппарата в пространстве система должна иметь не менее двух групп чувствительных элементов, направленных на два различных небесных тела, например, на две звезды.
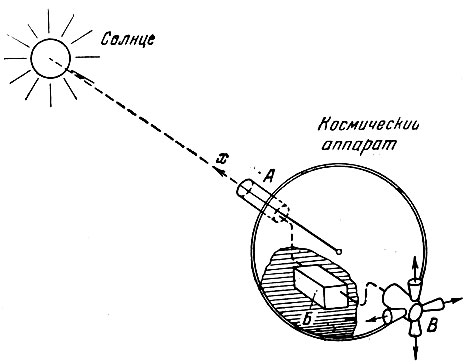
Рис. 47. Схема системы ориентации космического аппарата на Солнце А - чувствительный элемент системы; Б - усилительно-преобразующее устройство; В - органы управления; х - ось ориентации на Солнце
В качестве органов управления на космическом аппарате могут быть использованы миниатюрные реактивные двигатели, установленные таким образом, чтобы при включении одного из них создавался момент реактивной силы относительно соответствующей оси аппарата, проходящей через его центр масс. При помощи системы таких двигателей можно управлять движением аппарата относительно его поперечных и продольных осей.
Другим способом является использование специальных вращающихся маховиков. Если начать вращать маховик, расположенный на космическом аппарате, то сам аппарат при отсутствии каких-либо внешних воздействий начнет вращаться в обратном направлении. При этом угловые скорости вращения и углы поворота аппарата и маховика (в не вращающейся системе координат), исходя из условия сохранения кинетического момента системы аппарат - маховик, будут обратно пропорциональны их моментам инерции. Имея на космическом аппарате три маховика с взаимно-перпендикулярными осями вращения, можно управлять его движением относительно центра масс.
Источники энергии для питания бортовой аппаратуры
Одной из технических проблем при создании космических аппаратов является проблема энергопитания.
Космические аппараты не имеют возможности снабжаться энергией с Земли. Поэтому энергия для питания их аппаратуры может быть получена либо путем накопления перед пуском достаточно больших ее запасов (например, в аккумуляторных батареях), либо путем использования имеющейся в космическом пространстве энергии солнечного излучения. Принципиально можно представить себе также применение на космических аппаратах энергетических установок с ядерными реакторами-своего рода малых атомных электростанций.
Однако вес таких установок, по-видимому, будет весьма значительным, и они могут быть применены только на достаточно больших космических кораблях или спутниках-станциях.
Возможности накопления в аккумуляторах больших запасов энергии, обеспечивающих длительную работу бортовой аппаратуры, весьма ограничены.
Лучшие из электрохимических источников энергии, по литературным данным, характеризуются емкостью не более 0,1 квт-ч на 1 кг веса. Исходя из этой цифры, можно определить вес источников питания на месяц работы бортовой аппаратуры в зависимости от ее средней мощности (табл. 24).
| Средняя мощность аппаратуры, вт | Вес источников питания на месяц работы аппаратуры, кг |
|---|---|
| 10 | 75 |
| 20 | 150 |
| 50 | 375 |
| 100 | 750 |
| 200 | 1500 |
Из приведённых данных следует, что при использовании электрохимических источников питания время работы аппаратуры, при сколько-нибудь значительной ее мощности, весьма ограничено.
Одним из путей решения задачи энергопитания бортовой аппаратуры в течение длительного времени является непосредственное преобразование лучистой энергии Солнца в электрическую энергию в полупроводниковых фотоэлектрических генераторах, называемых обычно солнечными батареями.
Солнечная батарея состоит из большого количества одинаковых элементов, каждый из которых представляет тонкую пластинку, вырезанную из сверхчистого монокристаллического кремния. Кремниевые пластинки подвергаются специальной обработке.
Один из способов обработки заключается в образовании поверхностного слоя кремния так называемого N-типа путем термической диффузии фосфора из газовой фазы. После обработки каждая пластинка состоит из двух областей Р и N, имеющих противоположные механизмы проводимости (рис. 48). При освещении пластинки солнечными лучами между этими областями возникает разность потенциалов. Напряжение, создаваемое отдельными элементами, составляет примерно 0,5 в. Соответствующее соединение элементов позволяет получить необходимые величины напряжения и силы тока.
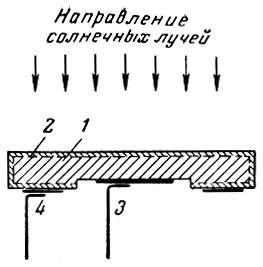
Рис. 48. Схема элемента солнечной батареи: 1 - монокристаллический кремний Р-типа; 2 - поверхностный слой - кремний N-типа; 3 и 4 - электроды
Отдельные кремниевые пластинки конструктивно объединяются в секции, собираемые на панелях. Кремниевые солнечные батареи имеют коэффициент преобразования около 10%, что позволяет в условиях космического пространства получить электрическую мощность до 100 вт с 1 м2 поверхности батареи.
Получаемый от солнечной батареи постоянный ток сравнительно невысокого напряжения без труда может быть трансформирован в переменный или постоянный ток требуемого напряжения с помощью специальных преобразователей. В систему энергопитания космического аппарата, снабженного солнечной батареей, должна быть включена также так называемая буферная аккумуляторная батарея (рис. 49). Буферная батарея обеспечивает поддержание энергетического баланса при переменном потреблении энергии бортовой аппаратурой. На искусственных спутниках Земли буферная батарея заряжается в периоды, когда спутник освещен Солнцем и осуществляет питание аппаратуры в те периоды, когда спутник находится в тени Земли.
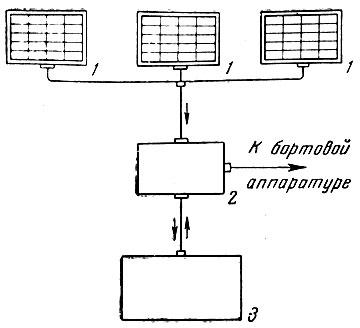
Рис. 49. Система энергопитания с солнечной батареей: 1 - солнечная батарея; 2 - коммутирующее устройство; 3 - буферная аккумуляторная батарея
Общая продолжительность работы такой системы практически будет определяться лишь сроком исправной работы отдельных ее деталей и, в частности, кремниевых элементов, которые с течением времени могут выходить из строя вследствие метеорной эрозии.
Преимущества использования на искусственных спутниках солнечных батарей возрастают с увеличением времени работы аппаратуры. Так, солнечная батарея площадью 1,5м2, со средней мощностью 100 вт, при времени работы 6 месяцев эквивалентна системе питания с электрохимическими источниками тока общим весом не менее 4-5 т.
Опыт использования солнечных батарей на третьем советском искусственном спутнике Земли подтвердил их высокую эффективность и надежность. При рационально выполненной конструкции метеорная эрозия и перепады температур не представляют опасности для работы солнечных батарей. Системы энергопитания на основе солнечных батарей использовались также на советских автоматических межпланетных станциях.
Искусственные спутники и проблема межпланетных полетов
Впервые вопрос о возможности посылки космического корабля за пределы земной атмосферы был теоретически решен в начале XX столетия выдающимся русским ученым К. Э. Циолковским, доказавшим, что средством для космического полета должна быть ракета. К. Э. Циолковский разработал ряд основных проблем межпланетного полета, первым предложил схему ракеты, работающей на жидком топливе, и научно обосновал возможность получения космических скоростей с помощью составных ракет. Его по праву называют отцом астронавтики.
В эпоху, когда К. Э. Циолковский начинал свою деятельность, в начале XX в., отсутствовали реальные технические предпосылки для осуществления полетов в космическом пространстве. Однако он глубоко верил в могущество человеческого разума. "Человечество не останется вечно на Земле,- писал он,- но, в погоне за светом и пространством, сначала робко проникнет за пределы атмосферы, а затем завоюет все околосолнечное пространство".
В настоящее время мы являемся свидетелями решающего шага на пути к осуществлению этой грандиозной задачи.
Создание первых искусственных спутников и космических ракет следует расценивать как решающий практический шаг на пути к осуществлению межпланетных полетов в силу ряда причин.
Во-первых, запуск искусственных спутников и космических ракет знаменует собой достижение такого уровня развития ракетной техники, при котором оказывается возможным получить космические скорости, необходимые Для осуществления полетов за пределами земной атмосферы.
Во-вторых, создание последовательно усовершенствуемых космических аппаратов позволит исследовать и практически решить все основные проблемы, связанные с длительным пребыванием межпланетного корабля с людьми в космическом пространстве. Вместе с тем решение, например, такой задачи, как спуск людей и оборудования с искусственных спутников явится одновременно решением проблемы возвращения межпланетных путешественников из космического полета.
И наконец, в соответствии с современными представлениями, искусственные спутники Земли и планет необходимы в качестве промежуточных станций при осуществлении межпланетных полетов.
Остановимся подробнее на этом вопросе. Анализ перспектив межпланетных полетов приводит большинство современных авторов к выводу о неосуществимости полетов человека даже на ближайшие небесные тела (Марс, Венеру) с помощью одной ракеты - космического корабля, стартующего с Земли.
Основные трудности осуществления межпланетных полетов можно проиллюстрировать на примерах полетов на Луну и Марс. Схема таких полетов дана на рис. 50. Ориентировочные значения скоростей, которые должна развить ракета на отдельных этапах своего движения, а также значения суммарной, так называемой характеристической скорости, приведены в табл. 25.
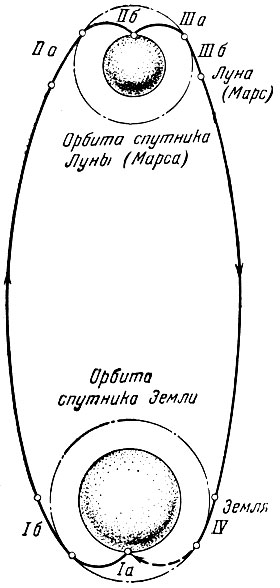
Рис. 50. Схема межпланетного полета: Участки полета: Ia - выведение на орбиту спутника Земли; Iб - отлет с орбиты спутника Земли; IIа - переход на орбиту спутника Луны (Марса); IIб - посадка на Луну (Марс); IIIа - выведение на орбиту спутника Луны (Марса); IIIб - отлет с орбиты спутника Луны (Марса); IV - переход на орбиту спутника Земли
| Требуемая скорость | Полет Земля - Луна - Земля | Полет Земля - Марс - Земля |
|---|---|---|
| При отлете с Земли: | ||
| а) для выведения на орбиту спутника Земли | 10,0* | 10,0* |
| б) для отлета с орбиты мпутника Земли | 3,0 | 3,4 |
| При посадке на планету: | ||
| а) для перехода на орбиту спутника планеты | 0,7 | 2,0 |
| б) для посадки на поверхность планеты | 2,0* | 4,5* |
| При полете с планеты: | ||
| а) для выведения на орбиту спутника планеты | 2,0* | 4,5* |
| б) для отлета с орбиты спутника планеты | 0,7 | 2,0 |
| При возвращении на Землю | 3,0** | 3,4** |
| Суммапная характеристическая скорость | 21,4 | 29,8 |
* (Приведенные значения скорости превышают скорости движения спутников на величину потерь, вызываемых влиянием силы тяжести на участке взлета или посадки.)
** (Имеется в виду изменения скорости, обеспечивающее переход на круговую орбиту, расположенную на высоте нескольких сот километров над поверхностью Земли. Дальнейший спуск может быть осуществлен без затраты топлива за счет использования аэродинамических сил.)
Из таблицы видно, что характеристическая скорость при полете на Луну составляет более 21 км/сек, а при полете на Марс - около 30 -км/сек.
Анализ возможностей ракетной техники показывает, что при использовании лучших химических топлив, или известных в настоящее время способов применения ядерной энергии ракеты, обладающие указанными характеристическими скоростями, должны иметь начальный вес, исчисляемый многими тысячами тонн.
Создание ракет столь большого веса лежит за пределами технических возможностей ближайшего будущего. Поэтому осуществление полетов на другие планеты по такой простейшей схеме, предполагающей старт космического корабля непосредственно с поверхности Земли, по-видимому, не представляется возможным, по крайней мере до тех пор, пока не будут найдены новые способы получения реактивной силы, отличные от применяемых в настоящее время.
Однако имеется другая схема осуществления межпланетных полетов - с использованием искусственных спутников Земли и планет в качестве промежуточных станций. Идея использования искусственных спутников при осуществлении межпланетных полетов была высказана еще К. Э. Циолковским и развита в работах ряда его последователей.
Один из возможных вариантов межпланетного полета представляется в этом случае следующим образом:
а) Создается искусственный спутник, движущийся по некоторой орбите вокруг Земли на достаточно большой высоте. Путем последовательных рейсов нескольких ракет осуществляется транспортировка на спутник запасов топлива и элементов конструкции космического корабля. Сборка космического корабля из отдельных элементов производится на орбите спутника.
б) Осуществляется перелет с орбиты спутника Земли к планете, являющейся целью путешествия. Космический корабль превращается в искусственный спутник этой планеты.
в) С созданного таким образом искусственного спутника планеты производится полет на ее поверхность с обратным возвращением. Для этого полета используется часть (одна из ступеней) космического корабля. Другая часть его, обеспечивающая в дальнейшем возвращение к Земле, продолжает в течение этого времени двигаться на орбите вокруг планеты.
г) Осуществляется перелет с этой орбиты к орбите искусственного спутника Земли.
д) Производится спуск пассажиров и необходимого оборудования с орбиты спутника Земли на ее поверхность. Этот этап полета может быть совершен почти без затраты топлива, в основном за счет использования аэродинамических сил.
Очевидными преимуществами такой схемы межпланетного полета является, во-первых, возможность накопления на искусственном спутнике Земли значительных запасов топлива и материалов для сборки космического корабля достаточно больших размеров и веса. При этом каждая из ракет, осуществляющих транспортировку необходимых материалов на орбиту искусственного спутника, может иметь не слишком большой начальный вес (например, порядка нескольких сот тонн).
Во-вторых, значительное уменьшение веса той части космического корабля, которая должна обеспечивать посадку кабины с пассажирами на планету, являющуюся целью путешествия, и отлет с нее. При осуществлении полета по первой схеме вес этой части космического корабля был бы в несколько раз большим, поскольку в полезную нагрузку, помимо кабины с пассажирами, включался бы и вес тех ступеней ракеты, которые необходимы для последующего возвращения к Земле.
И, в-третьих, возможность выбора для космического корабля конструктивной схемы, наиболее приспособленной к условиям полета за пределами атмосферы.
В частности, для космического корабля, осуществляющего перелеты между орбитами искусственных спутников (так называемого орбитального корабля), могут быть применены двигатели с тягой, значительно меньшей его веса. Это обстоятельство открывает реальные перспективы использования для орбитальных кораблей электрореактивных двигателей, что позволит существенно увеличить вес полезного груза.
Для более наглядного выяснения преимуществ осуществления межпланетных полетов по второй схеме приведем сравнительные оценки основных характеристик ракет для рассматриваемых схем полета. С этой целью воспользуемся формулой (1.43), определяющей зависимость между характеристической скоростью ракеты и отношением ее начального веса к весу полезной нагрузки при оптимальном числе ступеней.
Допустим, что скорость истечения реактивной струи с может достигать 4000÷5000 м/сек, а относительный вес конструкции α = 0,1, что соответствует весьма высокой степени совершенства конструкции ракеты.
Отношение начального веса составной ракеты к весу полезного груза в зависимости от характеристической скорости в этом случае может быть определено по графику, приведенному на рис. 51.
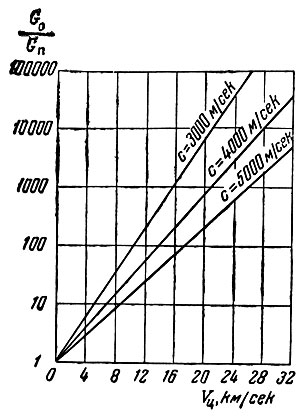
Рис. 51. Отношение начального веса ракеты к весу полезного груза в зависимости от характеристической скорости
На основании этого графика можно установить, что при весе полезного груза (кабины с пассажирами и необходимым оборудованием) Gп - 10 m и с - 4000 м/сек стартовый вес ракеты, с помощью которой можно было бы осуществить полет на Луну по первой схеме, должен составлять около 10 000 m. Для полета на Марс при тех же условиях потребовалась бы ракета весом свыше 180000 m. При с = 5000 м/сек стартовые веса составят: для полета на Луну - около 3000 m, для полета на Марс - более 25 000 m.
Рассмотрим теперь, какими характеристиками при тех же условиях должны обладать ракеты при осуществлении полета по второй схеме. Основные характеристики таких ракет, в предположении использования двигателей со скоростью истечения с = 4000 м/сек при относительном весе конструкции ступеней ракет α = 0,1, приведены в табл.26. При этом отношение начального веса ракет, обеспечивающих получение необходимых скоростей на отдельных этапах полета, к весу их полезного груза также определялось по графику, приведенному на рис. 51. Из данных табл. 26 видно, что при полетах на Луну и Марс суммарный вес топлива и элементов конструкции при переходе от первой ко второй схеме осуществления полета уменьшается соответственно в 2 и 4,5 раза. При второй схеме первый этап полета может быть реализован путем запуска ряда грузовых ракет весом в несколько сот тонн каждая, в то время как при первой схеме полета необходимо создание космических кораблей, способных стартовать с поверхности Земли и обладающих начальным весом в тысячи и десятки тысяч тонн.
| Основные характеристики | Полет Земля - Луна - Земля | Полет Земля - Марс - Земля |
|---|---|---|
| Ракеты для доставки элементов космического корабля на орбиту искусственного спутника Земли (участок полета Iа)* | ||
| характеристическая скорость, км/сек | 10 | 10 |
| начальный вес (суммарный), m | 5540 | 38400 |
| общий вес полезного груза, m | 205 | 1430 |
| Ракета для перелета на орбиту искусственного спутника планеты (участок полета Iб и IIа)* | ||
| характеристическая скорость, км/сек | 3,7 | 5,4 |
| начальный вес, m | 205 | 1430 |
| вес полезного груза, m | 61 | 242 |
| Ракета для спуска на поверхность планеты и подъема с нее (участки полета IIб и IIIа)* | ||
| характеристическая скорость, км/сек | 4,0 | 9,0 |
| начальный вес, m | 37 | 193 |
| вес полезного груза (кабины с экипажем и оборудованием), m | 10 | 10 |
| Ракета для перелета на орбиту искусственного спутника Земли (участки полета IIIб и IV)* | ||
| характеристическая скорость, км/сек | 3,7 | 5,4 |
| начальный вес, m | 34 | 59 |
| вес полезного груза (кабины с экипажем и оборудованием), m | 10 | 10 |
* (Участки полетов указаны на рис. 50.)
Приведенные данные наглядно показывают преимущества, получаемые при использовании искусственных спутников в межпланетных полетах.
Несомненно, что осуществление межпланетных полетов с использованием искусственных спутников потребует решения ряда чрезвычайно сложных технических проблем. К таким проблемам в первую очередь относятся: осуществление точного выведения большого числа транспортных ракет на орбиту спутника-станции, их сближение и сборка космического корабля в межпланетном пространстве, навигация при осуществлении перелетов между орбитами искусственных спутников и др. Однако этот путь является в настоящее время, по-видимому, единственным, открывающим реальные перспективы осуществления межпланетных полетов.
Заглядывая в будущее, можно представить основные этапы освоения человеком полетов на другие небесные тела:
а) предварительное исследование основных проблем космического полета на автоматических искусственных спутниках Земли. Осуществление космических полетов ракет с автоматически работающей аппаратурой;
б) создание искусственных спутников Земли с людьми и постоянно существующих искусственных спутников-станций. Детальная отработка на них всех основных вопросов космического полета. Решение проблемы спуска людей и оборудования со спутника на Землю;
в) совершение человеком полетов к Луне и ближайшим планетам без посадки на их поверхность;
г) переход к межпланетным полетам. Последовательное изучение отдельных планет солнечной системы путем организации экспедиций на них.
Из всего сказанного очевидно огромное значение искусственных спутников для осуществления полетов на другие небесные тела.
|
ПОИСК:
|
© 12APR.SU, 2010-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://12apr.su/ 'Библиотека по астрономии и космонавтике'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://12apr.su/ 'Библиотека по астрономии и космонавтике'