
Приложения
Приложение 1. Основные зависимости движения в центральном поле тяготения
Интегрирование уравнений движения материальной точки в центральном поле тяготения
Уравнения движения имеют вид (см. главу I):
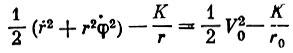 (1)
(1)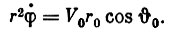 (2)
(2)Согласно второму уравнению
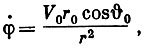 (3)
(3)
но 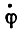 можно представить в виде:
можно представить в виде:
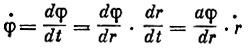
и, следовательно,
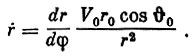 (4)
(4)Подставив (3) и (4) в уравнение (1), получим:
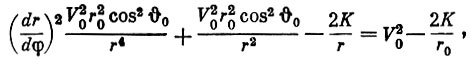
откуда
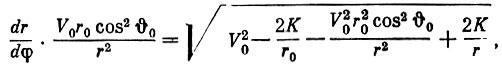
или
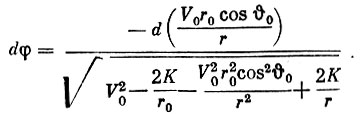
Для удобства интегрирования введем постоянную величину 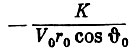 знак дифференциала в числителе, а также прибавим и вычтем величину
знак дифференциала в числителе, а также прибавим и вычтем величину
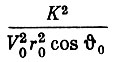
в подкоренном выражении.
В результате получим:
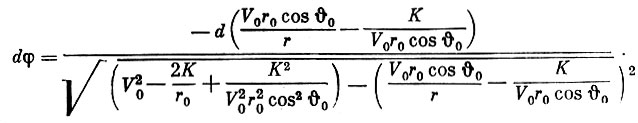 (5)
(5)Интегрирование этого выражения приводит к уравнению орбиты:
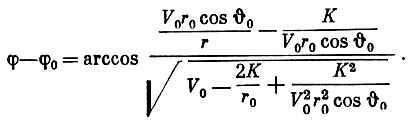 (6)
(6)Здесь φ0 - постоянная интегрирования - зависит от начала отсчета углов φ.
Уравнение орбиты (6) можно представить в виде:
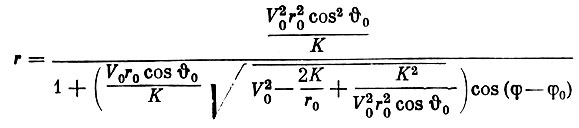 (7)
(7)или, введя обозначения
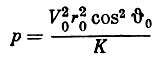 (8)
(8)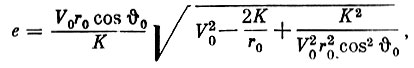 (9)
(9)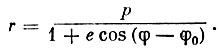 (10)
(10)Определение периода обращения по эллиптической орбите
Секториальная скорость материальной точки, движущейся по эллиптической орбите в центральном поле тяготения, постоянна и равна 1/2 V0r0 cos  0 (см. главу I), а площадь, охватываемая эллиптической орбитой (площадь эллипса), составляет πаb, где а и b - соответственно большая и малая полуоси эллипса.
0 (см. главу I), а площадь, охватываемая эллиптической орбитой (площадь эллипса), составляет πаb, где а и b - соответственно большая и малая полуоси эллипса.
Следовательно, период обращения (время полного оборота точки по орбите) будет равен:
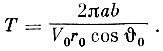 (11)
(11)Для эллипса имеем:
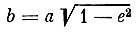
и
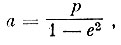
откуда
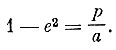
и, следовательно,
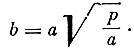 (12)
(12)Подставив в (11) значение b из (12) и р из (8), получим после элементарных преобразований формулу, определяющую период обращения:
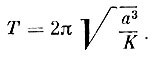 (13)
(13)Приложение 2. Ракетные исследования верхней атмосферы
Ракеты (рис. 1) как инструмент для проведения геофизических, физических и астрофизических исследований начали применяться в 1946 г. Программа ракетных исследований охватывала многие вопросы физики верхних слоев атмосферы. Остановимся на некоторых результатах этих исследований, а также на методической стороне эксперимента.
Изучение состава атмосферы
На основании закона парциальных давлений следует, что в гравитационном поле Земли должно изменяться с высотой процентное содержание легких газов в атмосфере, т. е. более легкие газы должны преобладать в области больших высот, а более тяжелые располагаться ниже. Поэтому состав воздуха на различных высотах должен быть различен. В результате проведенных теоретических исследований было показано, что уровень гравитационного разделения газов в атмосфере должен находиться на высотах порядка 80-100 км. Достижение таких высот стало возможно только с использованием ракет.
В период с 1951 по 1961 г. в Советском Союзе проводились исследования по определению состава воздуха на больших высотах. С этой целью была разработана специальная методика взятия проб воздуха во время полета ракеты. Химический состав проб воздуха после спуска ракеты на Землю определяется в лаборатории посредством спектрального анализа. В итоге многих измерений установлено, что до высот порядка 95 км не замечается различий в соотношении кислорода и азота по сравнению с их соотношением на уровне земной поверхности. Можно утверждать с достаточной точностью, что атмосферу до высоты 100 км следует считать кислородно-азотной.
Изучение давления, плотности и температуры
Поскольку для верхней атмосферы остается справедливым максвелловское распределение скоростей молекул, можно определять температуру, давление и плотность, используя уравнение состояния для идеального газа:
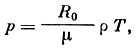 (1)
(1)где р - давление, ρ - плотность, Т - температура, пропорциональная средней кинетической энергии движения молекул газа, μ - молекулярный вес, R0 - газовая постоянная.
Кроме того, до указанных высот, по-видимому, имеет место гидростатическое уравнение:
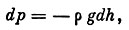 (2)
(2)где g - ускорение силы тяжести, h - высота над уровнем моря.
Используя уравнения (1) и (2) и измерив один из трех параметров (p, ρ, T), можно найти два других. Точность результата при этом способе измерения зависит от точности дифференцирования или интегрирования экспериментальной кривой, а также от знания распределения молекулярного веса μ(h) с высотой, т. е., по существу, от газового состава, о котором говорилось выше.
Непосредственное измерение указанных параметров, например давления, на движущейся ракете крайне затруднительно, так как при этом измеряются не параметры среды, а параметры потока разреженного газа, в котором движется ракета, что вносит существенные ошибки в измерения. Появление ударных волн перед ракетой и приборами при сверхзвуковом потоке вносит ряд дополнительных трудностей.
Для устранения целого ряда искажающих факторов были предприняты попытки продувкой модели ракеты определять на ней места, где давление мало отличается от статического, и здесь устанавливать манометры.
Путем изучения функции продувки
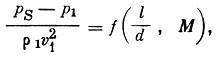 (3)
(3)где pS - давление в некоторой точке поверхности ракеты; ρ1, p1,
М - плотность, давление и число Маха невозмущенного потока;
l/d - отношение расстояния от носка ракеты до рассматриваемой
точки к диаметру, ракеты; v1 - скорость ракеты, можно найти места на ракете, где pS = р1 (f = 0), т. е. давление в некоторой точке ракеты равняется давлению невозмущенного потока.
Манометры устанавливаются в точках, где pS = p1.
Аналогичным методом можно измерить и температуру, зная давление в двух точках обтекаемой поверхности. Отношение давления на расстоянии х от носка ракеты (рх) к статическому давлению р в невозмущенном потоке есть функция:
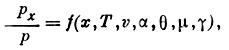 (4)
(4)
где v - скорость ракеты, α - угол атаки, θ - угол поворота, μ - молекулярный вес, 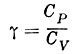 - отношение теплоемкостей.
- отношение теплоемкостей.

Рис. 1. Ракета
Измеряя давление рх в двух точках х = а и х = b, получим отношение:
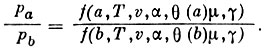 (5)
(5)Вид функций f(а,...) и f(b,...) определяется путем продувки. Если считать μ и γ постоянными (до высоты 80 км) и измерить значения v, α, θ(a), θ(b), то из выражения (5) можно найти значение Т.
Таким способом были рассчитаны температуры для высот 30- 70 км. Определив число М для невозмущенного потока, можно рассчитать температуру по формуле:
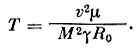 (6)
(6)Соображения, изложенные выше, приводят к следующему соотношению для определения плотности:
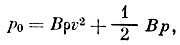 (7)
(7)где р0 - давление торможения при нулевом угле атаки, р - давление в покоящейся среде и
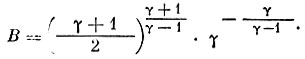 (8)
(8)Газодинамическая формула (7) справедлива примерно до высоты 100 км.
Для высот более 100 км справедлива при ряде упрощающих предположений формула:
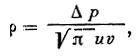 (9)
(9)где Δр - изменение давления за оборот ракеты вокруг оси; v - максимальная составляющая скорости, перпендикулярная плоскости отверстия манометра; u - наиболее вероятная скорость молекул в манометре.
Таким образом можно измерить термодинамические параметры атмосферы с помощью приборов, установленных на ракете.
Советские ученые разработали специальные отделяющиеся от ракеты контейнеры с аппаратурой, применение которых позволило исключить влияние корпуса ракеты на показания приборов, что явилось дальнейшим усовершенствованием постановки экспериментов.
Приборный контейнер помещается в мортиру, укрепленную на боковой поверхности тела ракеты и прикрытую в передней части обтекаемым колпаком. На заданной высоте, когда двигатель ракеты закончил свою работу и ракета движется по инерции, контейнер выбрасывается из мортиры. Получив небольшую, дополнительную (относительно ракеты) скорость, он уходит вперед, отклоняясь несколько в сторону и находясь все время в незагрязненном газами ракеты воздухе. Программный механизм включает в нужное время те или иные приборы, показания которых непрерывно регистрируются на фотопленке. Достигнув предельной высоты, контейнер падает. В 10-12 км над земной поверхностью автоматически открывается парашют, и контейнер плавно опускается на Землю (рис. 2).

Рис. 2. Контейнер
На основании полученных данных давления были построены кривые изменения температуры, рассчитанные по барометрической формуле:
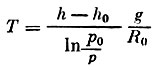 (10)
(10)в предположениях, что μ = 29 и состав воздуха до высоты 100 км постоянен (рис. 3).
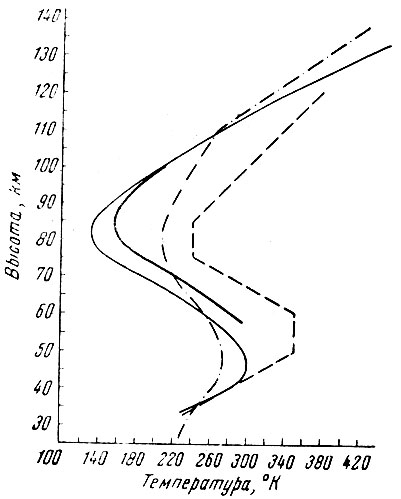
Рис. 3 Кривые изменения температуры
В совокупности с температурой и составом плотность определяет давление, если только время изменения одного из указанных параметров не слишком отличается от времени установления равновесного значения для других. Однако неизвестно, каково время установления равновесного состояния этих параметров на больших высотах.
Распределение температуры на больших высотах требует анализа со специальной точки зрения. Одной из важных проблем физики верхних слоев атмосферы является соотношение между газокинетической и вращательной температурами молекул. Под первой понимают среднюю кинетическую энергию поступательного движения молекул, а под второй - среднюю энергию их вращательного движения. В газе, находящемся в равновесном состоянии, эти температуры равны.
Таким образом, для верхних слоев атмосферы не ясны такие, казалось бы, простые вопросы, как закон изменения плотности с высотой, связь между температурой, давлением, плотностью и молекулярным составом, соотношение между кинетической и вращательной температурами. Все это является следствием более общей проблемы статистического равновесия в атмосфере. Поэтому важнейшим вопросом физики верхней атмосферы является изучение времени релаксации и молекулярного механизма тех процессов, благодаря которым атмосфера стремится принять равновесное состояние, отвечающее определенным внешним условиям.
Несмотря на неполноту наших знаний о физических параметрах верхней атмосферы, ракетные измерения дали значительный экспериментальный материал, на основании которого в настоящее время делаются попытки построения физической модели верхней атмосферы.
Ионосферные измерения
Отражения радиоволн позволяют определить изменение электронной концентрации с высотой вплоть до максимального значения. Выше максимума слоя электронной концентрации это изучение делается невозможным.
С помощью ракетного зондирования можно измерить коэффициент преломления п как функцию высоты для радиоволн любой выбранной длины волны, а из показателя преломления можно найти электронную концентрацию N(h); при этом существенное значение имеет то обстоятельство, что вертикальные перемещения источников излучения должны превышать их горизонтальные перемещения.
Если плоская монохроматическая электромагнитная волна с частотой со распространяется в ионизированной среде, находящейся в магнитном поле, то можно связать диэлектрическую проницаемость ионизированной среды с показателем преломления по формуле:
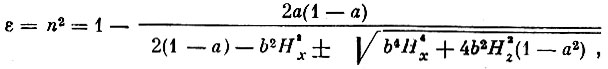 (11)
(11)где
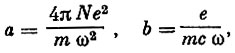
N - число свободных электронов в 1 см3,
m - масса частицы.
Если магнитное поле отсутствует (H = 0), то
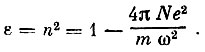 (12)
(12)В случае полного внутреннего отражения и при постоянной плотности ионизации n = 0.
Таким образом, при нормальном падении в случае полного внутреннего отражения волна возвратится в то место, из которого вышла. Зная состав отражающего слоя, мы можем найти отношение:
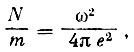 (13)
(13)а отсюда концентрацию электронов.
В присутствии магнитного поля формула (11) имеет два значения в соответствии со знаками перед радикалом, стоящим в знаменателе. Поэтому при прохождении через ионизированную среду электромагнитная волна расщепляется на две волны: обыкновенную (знак плюс) и необыкновенную (знак минус).
С помощью ракетных исследований удалось измерить в области от 80-85 до 200 км действительные части коэффициентов преломления, обыкновенной и необыкновенной волн. На основе этих данных были рассчитаны кривые зависимости электронной концентрации N от высоты h.
В Советском Союзе, начиная с 1954 г., проводились обширные ракетные исследования распределения по высоте электронной концентрации в ионосфере. В основу определения электронной концентрации были положены измерения дисперсии излучаемых с ракеты радиоволн по методу дисперсионного интерферометра, предложенному академиками Л. И. Мандельштамом и Н. Д. Папалекси.
На ракете были установлены два передатчика, излучавшие когерентные радиоволны с частотами ω1 и ω2 = pω1 На Земле (в двух пунктах) регистрировались разность фаз и уровень принимаемых сигналов. Одновременно проводилось радиозондирование ионосферы с помощью панорамной ионосферной станции.
Используемые в опытах частоты были равны:
ω1 = 48⋅106 гц; ω2 = 144⋅106 гц(р = 3).
Разность фаз принимаемых радиосигналов за счет их дисперсии (относимая к более высокой частоте) составляет:
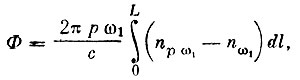 (14)
(14)где l - путь интегрирования от передающей до приемной антенн с = 3⋅1010см/сек.
Изменение Ф за отрезок от L до L + ΔL, имеет вид:
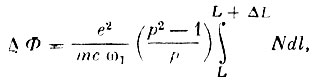 (15)
(15)а среднее значение N на пути ΔL:
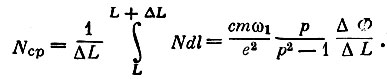 (16)
(16)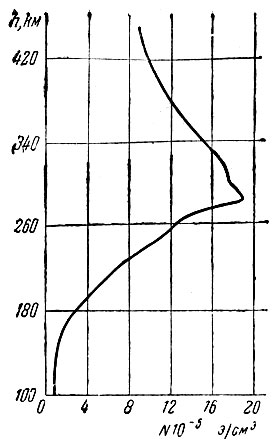
Рис. 4. Кривая распределения электронной концентрации N = f (h)
На основании описанной методики получены кривые распределения электронной концентрации N = f(h) до высот 105 и 210 км, а в пуске 21 февраля 1958 г. до высоты 465 км (рис. 4). Результаты измерений, относящиеся к области ниже максимума ионизации слоя F2 позволяют сделать вывод, что резко выраженного слоя Е ионосферы не существует. Это один из фундаментальных выводов ракетного зондирования ионосферы. Он проливает новый свет на представление о структуре ионосферы. Среди других исследований ионосферы важные сведения были получены (как в СССР, так и за рубежом) по химическому составу ионосферы с помощью нового прибора масс-спектрометра. Первые измерения с масс-спектрометром показали в пределах точности эксперимента (∼25%) отсутствие диффузионного разделения до высоты 137 км.
Дальнейшее применение масс-спектрометров дало первый ценный материал по природе ионов. Так, на высоте 93 км были зафиксированы ионы молекулярного кислорода, на высоте 106-107км ионы с атомным весом 12, 16, 21, 23, 26, 30 и 32. Кроме того, было впервые обнаружено наличие ионов натрия на высоте от 90 до 120 км. Одним из наиболее интересных фактов, полученных с помощью ракет, является решение вопроса, связанного с так называемой поправкой Лорентца в дисперсионной формуле. Сущность этого вопроса заключается в следующем: при движении электромагнитных волн в ионизированной среде в результате действия электромагнитного поля проходящей волны электроны, находящиеся в ионосфере, приходят в движение.
При этом неизвестно, достаточно ли принять в качестве ускоряющей силы, действующей на электрон, только электрический вектор падающей волны или учитывать еще силу, возникающую вследствие поляризации среды и дающую дополнительный член к основному полю в виде 4πσQ, где Q - вектор поляризации. Первое предположение согласуется с теорией дисперсии Зеллмейера (σ = 0), второе - с теорией поляризации Лорентца (σ - 1/3).
Расхождение, например в определении электронной концентрации, на основе той или другой теории достигает ∼ 50%
Многие попытки решить этот вопрос в ту или иную сторону не дали положительных результатов, и лишь в 1943 г. Дарвин и независимо от него В. Л. Гинзбург убедительно показали, что лорентцовой поправки учитывать не нужно.
Однако необходимо было экспериментально подтвердить полученные теоретические выводы.
Этот вопрос был окончательно решен при экспериментах, проведенных в США в 1949 г.
В результате эксперимента сравнивались значения наблюдаемых коэффициентов преломления с теоретическими кривыми (рис. 5), рассчитанными с учетом (а) и без учета (б) поправки Лорентца, Опыты показали, что поляризационный член следует опустить на частоте больше 4,274 Мгц.
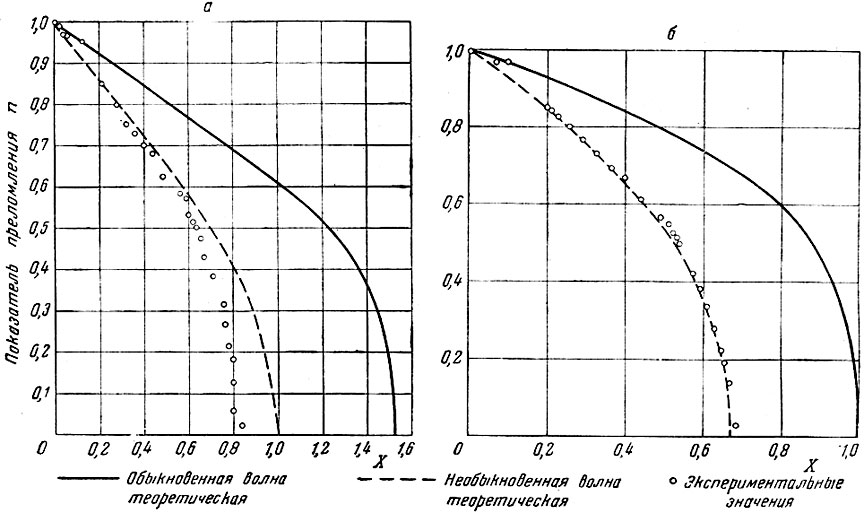
Рис. 5. Теоретические кривые
Наконец, следует отметить серию опытов по активному воздействию на верхние слои атмосферы. Эти опыты состоят в испарении паров натрия в атмосферу на высоте от 50 до 110 км. Было показано, что если несколько килограммов металлического натрия испарить в описанных выше условиях, то начинается бурная фотохимическая реакция с высвечиванием желтой линии натрия.
Принимая, что на высоте больше 100 км атмосферный кислород присутствует преимущественно в атомарном состоянии, можно, воздействуя на него специальным катализатором, искусственно создать процесс рекомбинации атомарного кислорода. Такой опыт был осуществлен в 1956 г. Во время полета ракеты несколько килограммов окиси азота было выпущено в атмосферу на высоте немного выше 100 км. Сразу же после выброса газа появилось сильно светящееся пятно. Оно постепенно распространялось, тускнея по мере расширения. Через 10 мин. оно покрыло площадь неба, эквивалентную трем диаметрам Луны, и перестало быть видимым невооруженным глазом. Предполагают, что результатом свечения было протекание следующих реакций:
 (a)
(a)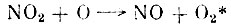 (б)
(б)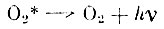 (в)
(в)Процесс (а) приводит к возникновению непрерывного спектра между 4000 и 7000 Å, а процесс (в) - к атмосферным полосам кислорода. Проведенные опыты открывают широкие возможности изучения химических процессов, протекающих в верхней атмосфере. Одной из них является нахождение реакции, в которую вовлекается атомарный азот, что позволит изучить фотохимическим способом концентрации) этой составляющей па различных высотах.
Исследование коротковолнового излучения Солнца
Одной из важных задач при изучении коротковолновой части спектра Солнца является определение зависимости интенсивности излучения от длины волны в солнечном спектре до поглощения солнечного излучения верхними слоями атмосферы. Измерения, производимые на Земле (на уровне моря), позволяют регистрировать излучения с длинами волн, превышающими 2900 Å. Остальная часть солнечного спектра полностью поглощается атмосферой и до поверхности Земли не доходит. Поглощенная энергия Солнца расходуется на образование ионосферы, слоя озона, свечение ночного неба, "круговых токов", которые текут в ионосфере и создают магнитные вариации, и т. д.
Измерение, солнечной радиации на Земле в интервале длин волн λ∼ 2900 Å и выше приводит к выводу, что распределение интенсивности излучения Солнца примерно соответствует излучению абсолютно черного тела при температуре 6000° К. Это предположение экстраполировалось и на коротковолновую часть спектра Солнца, т. е. считалось, что в интервале длин волн, не наблюдаемых на поверхности Земли, интенсивность остается такой же, как в случае эквивалентного черного тела.
Прямые ракетные измерения внесли существенные коррективы в наши представления о физике Солнца. На ракетах поднимались спектрографы специальной конструкции, с помощью которых производилась фоторегистрация спектра Солнца. В этих экспериментах было обнаружено, что с подъемом приборов на все большую высоту регистрируется все более коротковолновая часть спектра Солнца, вплоть до рентгеновских лучей.
Следует отметить также, что была снята линия Lα- Лаймана-альфа серии водорода с λ;∼ 1215 Å.
Результаты этих измерений показывают, что для ультрафиолетовой области спектра интенсивность падающего солнечного излучения заметно уменьшается и оказывается ниже, чем это соответствует излучению абсолютно черного тела. Однако в области мягких рентгеновских лучей (λ;∼ 1÷50 Å) интенсивность оказывается значительно больше, чем для абсолютно черного тела. Это, вероятно, является следствием излучения солнечной короны, кинетическая температура которой достигает 1 000 000° К.
Построенная на основе ракетных измерений кривая распределения интенсивностей в коротковолновой части спектра Солнца позволила уточнить солнечную постоянную, которая уже на высоте 65 км оказалась равной ∼ 2,0 кал/см2 мин. (ранее принималось значение 1,94 кал/см2мин.).
Изучение коротковолновой радиации Солнца на ракетах является, таким образом, мощным средством расширения наших познаний о структуре солнечной атмосферы.
Магнитные измерения
Напряженность магнитного поля Земли в какой-либо точке Р можно представить в виде уравнения:
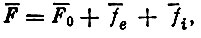 (17)
(17)где F0 - напряженность основного поля Земли;
fe -напряженность, вызванная изменением систем электрических токов над Землей, fi - соответственно внутри Земли. При этом rot fе = 0 внутри Земли, a rot F0 = 0 и rot fi = 0 вне Земли.
На значительной глубине внутри Земли:
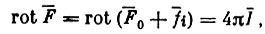 (18)
(18)а над поверхностью Земли:
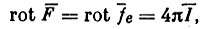 (19)
(19)где I - объемная плотность тока.
На основании гармонического анализа значение F на поверхности Земли мы можем представить как сумму F0, fe, fi и вычислить F0 + fi в любой точке над поверхностью Земли и fе внутри Земли. Однако в принципе оказывается невозможным по измерениям F на поверхности Земли оценить fе над поверхностью Земли и определить распределение силы токов I наверху. Можно предложить много систем токов I, создающих данное распределение fe на поверхности Земли, индуцирующих ту же самую систему внутренних токов и их поле fi.
Таким образом, с помощью только наземных измерений задача об определении источников переменной части магнитного поля не решается однозначно.
С момента открытия ионосферы и установления взаимосвязи изменений магнитного поля с состоянием ионосферы было сделано предположение, что источниками магнитных бурь и суточных вариаций являются электрические токи, текущие в ионосфере. С другой стороны, есть основания предполагать, что главные фазы бурь обусловлены системой токов в форме замкнутого экваториального кольца, на расстоянии нескольких земных радиусов от центра Земли. Таким образом, изучение магнитного поля Земли покоится пока на некоторых гипотетических предположениях, которые нуждаются в серьезной экспериментальной проверке.
Применение ракет впервые открыло возможность экспериментального обнаружения токовых систем. Было показано, что с помощью магнитометра, установленного на ракете, при вертикальном пересечении токового слоя (если он существует) можно будет отметить его по разрыву горизонтальных компонент магнитного поля на границах слоя.
С этой целью в США было осуществлено два эксперимента по запуску ракет вблизи геомагнитного экватора (υ = 11° S; λ = 89°W) в разное время. На борту ракет находились специально сконструированные магнитометры, измеряющие скалярную величину магнитного поля, независимо от ориентации ракеты. Во время второго полета (полет совершался в полдень) на высоте 93-105 км было отмечено резкое изменение в напряженности поля порядка 4 ± 0,5 мгс (рис. 6). Предполагается (Чепмен), что это изменение эквивалентно скачку в изменении горизонтальных компонент поля при прохождении через токовый слой.
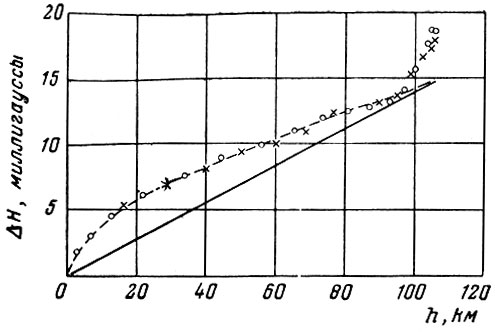
Рис. 6. Изменения напряженности поля порядка 4 ± 0,5 мгс
Этот скачок в изменении поля соответствует тому, который мог бы ожидаться при прохождении магнитометра через токовую систему суточных вариаций в области экватора.
Приложение 3. Определение плотности атмосферы по наблюдениям за эволюцией орбиты спутника
При движении спутника со скоростью v в среде с плотностью р спутник испытывает аэродинамическое сопротивление:
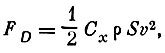 (1)
(1)где Сх - коэффициент сопротивления, S - поперечное сечение
спутника (его модель).
Рассмотрим для простоты круговую орбиту. В этом случае сила сопротивления FD действует так, что спутник приближается к Земле по спиралевидной траектории, а изменение энергии за оборот по орбите составит:
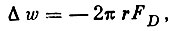 (2)
(2)где r - радиус орбиты.
С другой стороны, в случае движения по окружности мы имеем:
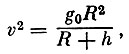 (3)
(3)где R - радиус Земли, h - высота орбиты, g0 - ускорение у поверхности Земли.
Таким образом выражение (2) примет вид:
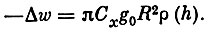 (4)
(4)Это выражение легко преобразовать, если воспользоваться связью между изменением общей энергии и высотой орбиты:
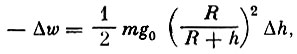 (5)
(5)после чего потери высоты орбиты за период можно представить так:
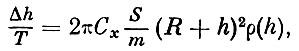 (6)
(6)где Т - период обращения спутника по орбите, m - масса спутника.
Подставляя полученное выражение вместе с численными значениями в третий закон Кепплера и интегрируя, найдем время, необходимое для опускания спутника с высоты h1 до h2:
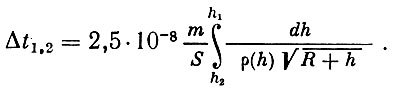 (7)
(7)Таким образом, задаваясь определенным значением отношения S/m и определяя достаточно точно значения Δt, можно найти закон изменения ρ с высотой h в случае круговой орбиты движения спутника. В случае эллиптической орбиты плотность можно измерять, исследуя вековые изменения в элементах орбиты.
Известно, что влияние атмосферы на вековые возмущения элементов орбиты сказывается прежде всего на вековых возмущениях большой полуоси а и эксцентриситета е. Показано, что если эксцентриситет является достаточно малым, то скорость v практически можно считать постоянной вдоль орбиты, а колебания da/dt и de/dt на протяжении орбиты возникают только вследствие колебания плотностей р. В этом случае изменения а и е за один оборот описываются выражениями:
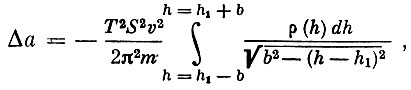 (8)
(8)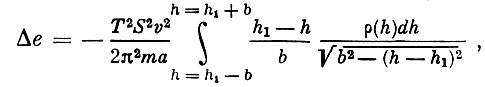 (9)
(9)где hi - средняя высота спутника, причем h1 - b и h1 + b соответственно высоты в перигее и апогее. Откуда
b = e(R + h).
Таким образом, используя уравнения (8) и (9), можно при достаточно точных измерениях Δа и Δе в последовательных оборотах определить p(h) на всех высотах между апогеем и перигеем.
Приложение 4. Особенности методики измерения давления и плотности при помощи манометров, установленных на спутнике
Вследствие разреженности верхней атмосферы взаимодействие быстр о летящего тела со средой будет происходить по законам свободномолекулярного течения.
Область так называемой молекулярной аэродинамики находится еще в начальной стадии своего развития из-за отсутствия многих физических данных. Однако можно, в первом приближении, считать, что:
а) распределение молекул по скоростям описывается функцией Максвелла;
б) отношение длины свободного пробега l молекул к характеристическому размеру обтекаемого тела L достаточно велико, т. е.
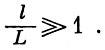
Если газ находится в термодинамическом равновесии, то, как показал Максвелл, все возможные скорости молекул должны быть распределены между молекулами по определенному закону: часть молекул будет иметь скорости, заключенные между с1 и с1 ± dс1, другая часть между с2 и с2 ± dc2 и т. д.
Для отдельно взятой молекулы существует вполне определенная вероятность того, что она имеет скорость в пределах с и с + dc. Обозначим через ξ, η, ζ компоненты скорости молекул. Согласно Максвеллу, число молекул, составляющие скорости которых по оси х находятся в пределах от ξ до ξ + dξ, будет равно:
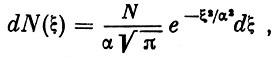 (1)
(1)где α - наиболее вероятная скорость, равная
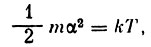 (2)
(2)N - число молекул в 1 см3, m - масса молекул, Т - температура. Аналогичные выражения получаются для других составляющих скоростей η и ζ.
Закон Максвелла для полной скорости имеет вид:
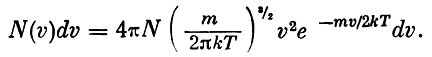 (3)
(3)Таким образом, число молекул N(v) в единице объема, скорости которых лежат в пределах v и v + dv, описывается функцией Максвелла.
На основании сделанных физических предпосылок можно установить ряд соотношений свободномолекулярного течения, играющих существенную роль в интерпретации показаний манометров.
Рассмотрим элемент площадки dS (см. рисунок), перпендикулярный оси х и движущийся со скоростью V относительно Земли. Тогда вектор V будет означать скорость набегающего потока газа относительно площадки dS.
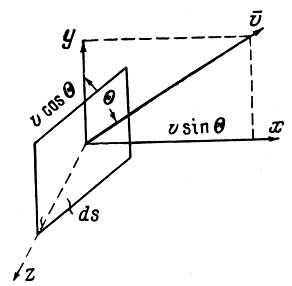
Рисунок. Элемент площадки
Будем считать, что распределение скоростей молекул газа подчиняется закону Максвелла.
В этом случае, чтобы найти полное число молекулу ударяющихся о единичный элемент площадки нужно проинтегрировать - ξNξηζdξdηdζ в пределах:
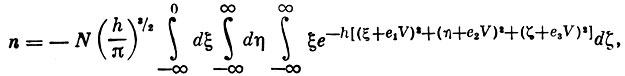
где h - величина, обратная квадрату наивероятнейшей скорости газа; е1, е2, е3 - направляющие косинусы. После интегрирования получим:
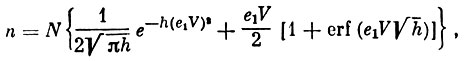 (4)
(4)
где 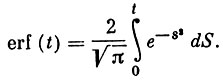
Обозначим через θ угол между осью у и вектором V, лежащим в плоскости элемента площадки dS. В этом случае:
е1 = sin θ; е2 = cos θ; е3 = 0.
Число молекул, ударяющихся в одну секунду об единичную площадку, будет равно:
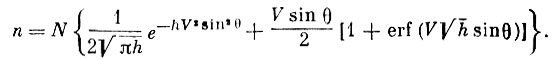
Так как 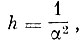 , то, обозначая
, то, обозначая 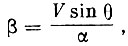 , окончательно получим
, окончательно получим
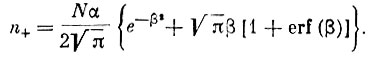 (5)
(5)Для догоняющего потока имеем:
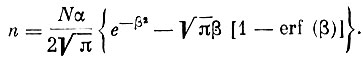 (6)
(6)Полученные выражения позволяют установить связь между давлением и числом частиц в единице объема полости манометра и соответствующими параметрами внешней среды.
Пусть спутник движется со скоростью V в среде с параметрами TV, Т, р, α; параметры газа в полости манометра будут N1, Т1, р1, α1. Изменение давления в объеме ω манометра за время dt за счет потока частиц, влетающих внутрь манометра, составит:
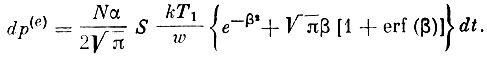 (7)
(7)Изменение давления за то же время за счет частиц, вылетающих из манометра, составит:
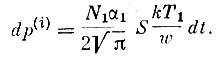 (8)
(8)Наконец, изменение давления за счет выравнивания температуры частиц, влетающих в манометр и находящихся в нем, составит:
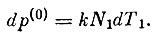 (9)
(9)Общее изменение давления будет равно:
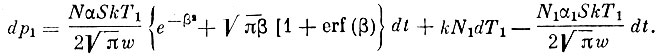 (10)
(10)
После этого из условия равновесия 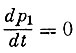 находим:
находим:
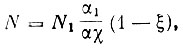
где: 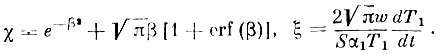
Как показывают оценки, величиной ξ можно пренебречь, и мы тогда получаем окончательное выражение:
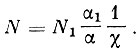 (11)
(11)Далее, давление в покоящейся среде равно:
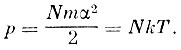
Подставляя в уравнение (11), получим
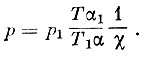 (12)
(12)В случае больших β имеем:
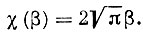
Используя для скорости α1 значение:
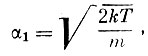
мы приходим к следующим выражениям
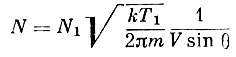 (13)
(13)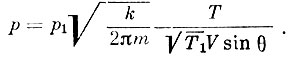 (14)
(14)Ориентация входного отверстия но отношению к вектору скорости спутника определяется по формуле:
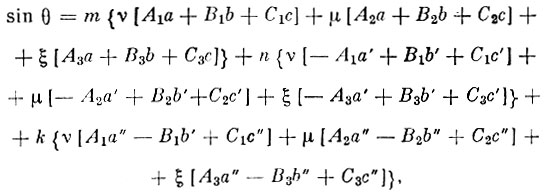 (15)
(15)где
Здесь ψ, φ, θ0 - углы Эйлера; ν, μ, ξ - направляющие косинусы вектора скорости в абсолютной системе координат; Ai, Bi, Сi - постоянные для данного витка; т, n, k - направляющие косинусы оси манометра относительно главных осей спутника.
Надо иметь в виду, что формулы (13) и (14) относятся к парциальным величинам.
Таким образом, для определения плотности и давления верхней атмосферы по формулам (13) и (14) необходимо знать абсолютную величину скорости спутника для каждого момента времени, ориентацию движения спутника для определения угла θ, а также его вращение относительно центра тяжести, температуру газа Т1 в манометре, массу частиц т. Все это представляет чрезвычайно сложную задачу.
Приложение 5. Принцип действия радиочастотного масс-спектрометра
Радиочастотный масс-спектрометр служит для определения ионного состава верхних слоев атмосферы. Рассмотрим принцип действия масс-спектрометрической трубки, состоящей из трех параллельных равноотстоящих друг от друга сеток. На эту систему сеток подается отрицательное пилообразное ускоряющее напряжение V*. Положительные ионы, попадая в трубку, ускоряются пилообразным напряжением до некоторой скорости
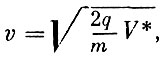
где q - заряд иона, m - его масса.
В случае однократного заряжения ионов эта скорость равна:
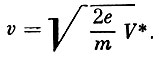
Кроме пилообразного напряжения, на среднюю сетку подается высокочастотное переменное напряжение с частотой ω = 2πf:
u = u0sin (ωt + θ), причем 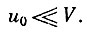 .
.
За счет высокочастотного поля ион получит дополнительное приращение энергии:
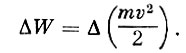
Так как изменение скорости мало, то
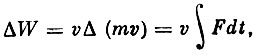
где F - сила, действующая па ион, когда оп находится в высоко частотном поле. Эта сила равна:
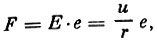
где r - расстояние между сетками. Таким образом:
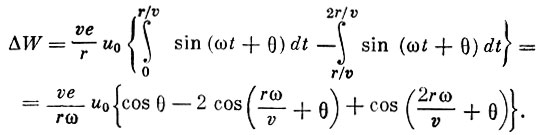 (1)
(1)
Отсюда видно, что приращение энергии иона за счет высокочастотного поля зависит от фазового угла θ и фазового угла 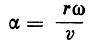 пролета ионом расстояния r. Кроме того, приращение энергии достигает максимума, когда
пролета ионом расстояния r. Кроме того, приращение энергии достигает максимума, когда 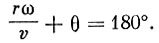 . В этом случае u = 0.
. В этом случае u = 0.
Таким образом,
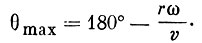 (2)
(2)Подставляя (2) в (1) и изменяя ω, получим, что ΔW достигает максимума при θ = 46°, т. е.
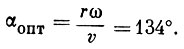
Следовательно, ион, подлетевший к первой сетке с фазой высокочастотного поля θ = 46° и пролетевший расстояние r со скоростью v, получит максимальное приращение энергии. Скорость иона зависит от массы и ускоряющего напряжения. Отсюда оптимальная скорость будет равна:
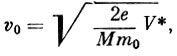 (3)
(3)где М - массовое число иона, m0 - масса атома водорода. Итак
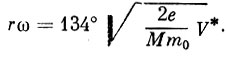
Отсюда
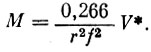 (4)
(4)Выражение (4) справедливо, если потенциал спутника равен нулю и скорость его также равна нулю. В общем случае имеем:
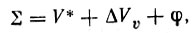 (5)
(5)где V*-ускоряющее напряжение, ΔVν - добавочное ускоряющее напряжение за счет скорости спутника, φ - потенциал спутника. При этом имеем:
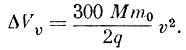 (6)
(6)Здесь v - скорость спутника.
Подставляя (5) в (4) с учетом (6), получим:
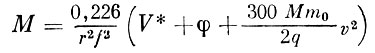
или окончательно:
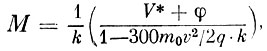 (7)
(7)где k - постоянная прибора, равная:
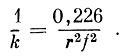
Если теперь на пути ионов, прошедших трехсеточную систему, поставить четвертую сетку, на которую подать подходящий тормозящий положительный потенциал uст то можно из всех ионов выделить лишь те, которые получили максимальное приращение энергии. Эти ионы достигнут коллектора, и прибор в цепи коллектора зарегистрирует пик ионного тока. Отмечая в этот момент значение пилообразного напряжения V*и потенциала спутника φ, можно по формуле (7) определить, какой массе соответствует данный пик.
Приложение 6. Особенности методики измерения концентрации положительных ионов на спутнике
Как и для разработки методики измерения давления верхних слоев атмосферы, в случае измерения концентрации положительных ионов, важно сформулировать основные физические предпосылки, на которых основано изучение структуры ионосферы.
В верхней атмосфере распределение ионов и электронов по скоростям подчиняется максвелловскому закону, а сумма концентраций отрицательных ионов и электронов равна сумме концентраций положительных ионов. Температура ионов Ti и электронов Те может быть различной. Обычно принимают, что Ti равна температуре нейтральных молекул, Те в ионосфере равна температуре газа Т.
Оценим время, в течение которого Те принимает значение Т в ионосфере.
Электронную температуру в момент ионизации можно выразить в виде:
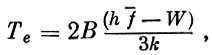
где f - среднее значение частоты; h = 6,63 ⋅ 10-27эрг ⋅ сек - постоянная Планка; k = 1,3805 ⋅ 10-16эрг/моль ⋅ град - постоянная Больцмана; В = 7730° К/эв; W - потенциал ионизации.
Как правило, в момент ионизации поглощается больше энергии, чем это требуется для ионизации атома или молекулы. Вследствие различия масс между ионом и электроном, эта избыточная энергия проявляется в виде кинетической энергии вырванного в момент ионизации электрона. При столкновении с более тяжелыми частицами этот избыток энергии теряется. Доля энергии, теряемая при каждом соударении электрона, определяется выражением:
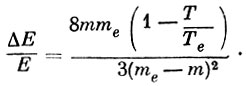 (1)
(1)Электронная температура и температура газа в слое F ионосферы связаны соотношением:
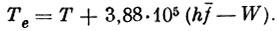 (2)
(2)
При условии, что 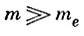 из выражений (1) и (2) следует:
из выражений (1) и (2) следует:
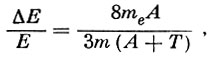 (3)
(3)где A = 3,88⋅105(hf - W). Предположим, что hf = 25 эв, W = 15 эв, М = 20, Т = 3000°.
В этом случае 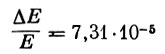 на одно соударение.
на одно соударение.
Если принять число соударений за одну секунду равным V= 2⋅103 1/сек., то Те будет равна Т через 25 сек. в слое F2. Отсюда можно заключить, что полученная в результате ионизации избыточная энергия электрона быстро распределится среди частиц газа и поэтому можно считать, что электронная температура Те равна Т - температуре газа в ионосфере. По различным оценкам принимается, что температура ионосферы Т = 1000°К. С другой стороны, по оценке В. Л. Гинзбурга, для слоя F2 ΔT = Te - Т ≈ 100 К, т. е. величины Те и Т практически одинаковы.
Тепловая скорость нейтральных молекул и ионов оценивается как vi≈105см/сек., а электронов ve≈107см/сек. Таким образом, скорость спутника (vсп = 8⋅105) больше скорости нейтральных молекул и меньше скорости электронов. Это имеет существенное значение при движении спутника в электронно-ионной плазме.
Различие скоростей ионов и электронов в плазме приводит к тому, что спутник при своем движении приобретает отрицательный заряд. Поле, которое создается отрицательно заряженным телом спутника, будет экранироваться слоем положительных пространственных зарядов. Этот слой не будет прилегать всюду к поверхности спутника, вследствие образования "молекулярной тени" позади спутника. Область тени будет заполняться электронами, что приведет к накоплению электронов за спутником. Это накопление будет продолжаться до тех пор, пока поле образовавшегося отрицательного пространственного заряда не воспрепятствует дальнейшему повышению в нем концентрации электронов. Таким образом, спутник вместе с областью "молекулярной тени" будет окружен слоем положительного пространственного заряда (см. рисунок).
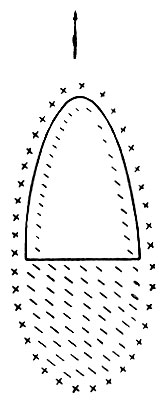
'Молекулярная тень'
Поскольку плазма электрически нейтральна, то для установления потенциала проводящей поверхности спутника должно выполняться условие
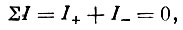 (4)
(4)где I+ - ток положительных ионов, I- - ток электронов. Ток положительных ионов определяется соотношением:
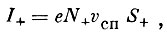 (5)
(5)где е - заряд электрона, N+ - концентрация положительных ионов, S+ - площадь проекции спутника на плоскость, нормальную вектору скорости.
Ток электронов при отрицательном потенциале спутника имеет вид:
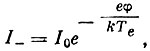 (6)
(6)где
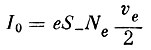
- электронный ток при φ = 0. Здесь S- - площадь проекции спутника на плоскость, нормальную магнитному меридиану, ve - тепловая скорость электронов.
Из последней формулы имеем:
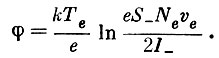 (7)
(7)Но, согласно формуле (4), I+ = I- и при отсутствии отрицательных ионов Ne = N+. Таким образом, окончательно имеем:
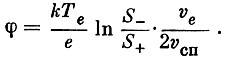 (8)
(8)При наличии тока фотоэмиссии с поверхности спутника Iф получаем следующее выражение для потенциала:
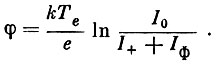 (9)
(9)Полученные значения потенциала спутника нужно рассматривать как если бы поверхность спутника была эквипотенциальной. Однако при движении спутника со скоростью vcп = 8⋅105км/сек в магнитном поле Земли поверхность спутника нельзя рассматривать, как эквипотенциальную. Разность потенциалов между двумя точками спутника на расстоянии ΔL, как показывают расчет, может достигать значения:
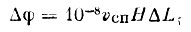
где Н - напряженность магнитного поля.
Таким образом, мы видим, что значение отрицательного потенциала спутника целиком определяется значением электронной температуры Те в ионосфере.
Для измерения концентрации положительных ионов используется метод, основанный на непрерывном измерении тока одного знака, который создается потоком заряженных частиц на поверхность спутника. С этой целью па спутнике устанавливаются две ионные ловушки с коллекторами. В случае отрицательного потенциала спутника ионный ток, создаваемый положительными ионами, пропорционален их концентрации:
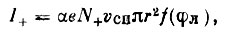 (10)
(10)где r - радиус сферической сетки ловушки, φл - потенциал ловушки относительно нейтральной плазмы, α - коэффициент. При φл = 0f (φл ) = 1. В этом случае
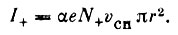 (11)
(11)Все величины, входящие в это выражение, кроме N+ - концентрации положительных ионов, известны, а поэтому возможно определение N+.
Следует отметить, что φл не всегда равно нулю, и может принимать как положительные, так и отрицательные значения. Чтобы воспользоваться для определения N+ формулой (11), поступают следующим образом: на поверхность сетки ловушки периодически подают от генератора импульсов биполярное напряжение и раз в несколько секунд снимают так называемые вольт-амперные характеристики
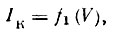 (12)
(12)где V = φ - φсп - разность потенциалов.
Чтобы теперь воспользоваться соотношением (11), необходимо на вольт-амперной характеристике найти точку, в которой φл = 0, и, следовательно, V = - φсп . Это можно сделать двумя способами: либо знать величину φсп в данный момент времени, либо определить некую характерную точку кривой (12), в которой φл - известна. Такая точка на кривой (12) существует: это точка торможения, т. е. точка, в которой φл соответствует полному торможению положительных ионов: φл = φт. С этого момента прекращается падение ионного тока при увеличении положительного потенциала сетки. При этом имеет место равенство:
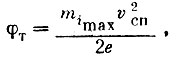
где mimax - масса наиболее тяжелых положительных ионов.
Поскольку величина V = φл - φсп, где φл = φт известна, мы будем знать φсп в этой точке. Отсюда можно найти точку кривой (12), где φл = 0, после чего по формуле (11) находим значение N(0)+ соответствующее этой точке.
Чтобы получить некоторое среднее значение концентрации положительных ионов, можно поступить следующим образом.
Найдем значения N(1)+ и N(2)+, соответствующие началу и концу подаваемого биполярного напряжения, положив в формуле (10) f (φл) = 1. Обозначим через 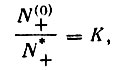 , где
, где 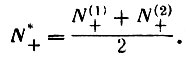
Если определить К1 и К2 по двум последовательным вольт-амперным характеристикам, то значения N+, определенные по ионным токам, зарегистрированным между снятием указанных характеристик, можно будет уточнить умножением на поправочный коэффициент
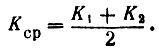
Возможен также другой способ определения на кривой (12) точки, где φл = 0, основанный на непосредственном измерении собственного заряда спутника.
Приложение 7. Основные теоретические предпосылки эксперимента по изучению коротковолновой части спектра солнца
Чтобы оценить распределение энергии в коротковолновой части спектра Солнца, можно поступить следующим образом.
Обозначим через Iv (0,  ) интенсивность излучения Солнца данной частоты v, выходящего под данным углом
) интенсивность излучения Солнца данной частоты v, выходящего под данным углом  относительно нормали к поверхности Солнца (рис. 1).
относительно нормали к поверхности Солнца (рис. 1).
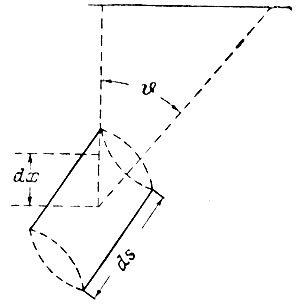
Рис. 1. Цилиндр
Пусть теперь луч света выходит с поверхности Солнца под углом  . Энергию, которую несет луч, создают внутренние слои Солнца, лежащие на различных глубинах. Рассмотрим один из таких слоев, характеризуемый температурой Т и находящийся на глубине х. Выделим в нем элементарный цилиндр (см. рис. 1) с высотой, равной
. Энергию, которую несет луч, создают внутренние слои Солнца, лежащие на различных глубинах. Рассмотрим один из таких слоев, характеризуемый температурой Т и находящийся на глубине х. Выделим в нем элементарный цилиндр (см. рис. 1) с высотой, равной

Тогда интенсивность излучения, испускаемая цилиндром, будет равна:
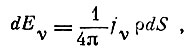
где ρ - плотность вещества внутри цилиндра, а jv - коэффициент излучения, рассчитанный на 1 г вещества.
При условий термодинамического равновесия можно написать, согласно закону Кирхгоффа:
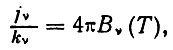
где kv - коэффициент поглощения, Bv (Т) - интенсивность излучения абсолютно черного тела, равная:
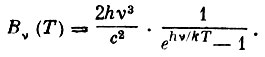
После этого
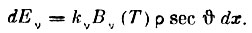
Часть этой энергии поглощается вышележащими слоями и поверхности Солнца достигает доля энергии dIv, определяемая выражением:
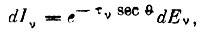
где τv - оптическая глубина слоя: 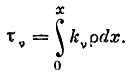 Интенсивность всего выходящего потока будет равна:
Интенсивность всего выходящего потока будет равна:
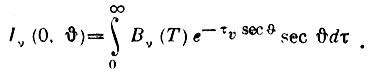 (1)
(1)Полный поток определяется соотношением:
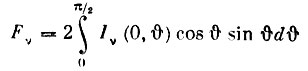
Или
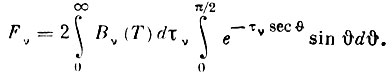 (2)
(2)Обозначим через Е2(х) функцию:
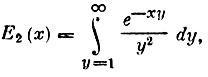
где положено у = sec  , a sin
, a sin 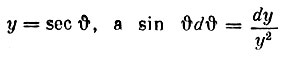 . Тогда выражение (2) примет вид:
. Тогда выражение (2) примет вид:
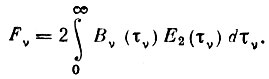 (3)
(3)С помощью формулы (3) Де Ягером было вычислено (при некоторых предположениях относительно модели фотосферы) распределение энергии в ультрафиолетовом участке спектра Солнца для длин волн между 2000 и 3000 А. Результаты этих вычислений вместе с экспериментальной кривой (сплошная линия) представлены на рис. 2. На основании полученных данных о распределении энергии в указанном интервале спектра можно судить о температурах в фотосфере. Однако для более коротких длин волн имеет место значительное расхождение между теоретической кривой Де Ягера и экспериментальной кривой.
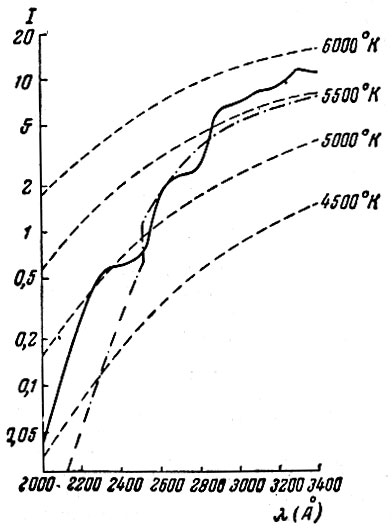
Рис. 2. Распределение энергии в ультрафиолетовом участке спектра Солнца для длин волн между 2000 и 3000
Для непрерывного спектра хромосферы в интервале длин волн 1040-1350 Å в предположении, что Солнце излучает в рассматриваемом участке длин волн как абсолютно черное тело, получены следующие значения температуры излучения:
Для 1040 - 1240 Å Т = 5500° ± 100°
1165 - 1265 Å Т < 4800°
1280 - 1340 Å Т = 5050° ± 100°.
Наиболее интенсивной линией в рассматриваемом спектро длин волн является линия лаймановской серии водорода Lα с λ = 1215 Å.По данным наблюдений, на границе земной атмосферы полное излучение этой линии имеет величину 0,10 ± 0,02 эрг⋅см-2⋅сек-1, что соответствует излучению поверхности Солнца ~ 4,6⋅103 ± 0,9⋅103эрг⋅см-2⋅сек-1.
Однако величина полной интенсивности Lα значительно колеблется, принимая значения от 0,1 до 10 эрг⋅см-2⋅сек-1. Указанные вариации линии Lα, очевидно, имеют место на самом деле даже при спокойном состоянии Солнца.
Теоретическое рассмотрение интенсивности излучения линии Lα и сравнение с данными эксперимента приводят некоторых авторов к выводу, что излучение Lα определяется не локальным значением электронной температуры, а формируется чистым рассеянием.
Полная интенсивность непрерывного излучения короны (по Элверту) равна 103эрг⋅см-2⋅сек-1 при Т = 106 °К. Для полного монохроматического излучения короны эта величина имеет порядок 2,5⋅103 Q эрг⋅см-2⋅сек-1, где Q - фактор неоднородности, который согласно исследованиям ряда авторов можно принять равным 2.
При увеличении температуры максимум излучения короны смещается по закону Вина (λmах⋅Т = const) в сторону более коротких длин волн. При температуре 6⋅105 °К этот максимум имеет место в области 80-90 Å, а при Т = 106 °К он смещается к 60 Å.
Все эти данные нуждаются в серьезной экспериментальной проверке. Особенно это относится к распределению интенсивности для участка спектра длин волн короче 100 Å, так как для этой части спектра длин волн, как показывают ракетные исследования, распределение энергии в спектре Солнца уже не соответствует равновесному излучению абсолютно черного тела. Представляет также значительный интерес экспериментальное изучение вариаций интенсивности и интенсивность излучения в непрерывном спектре за границей серии Лаймана.
|
ПОИСК:
|
© 12APR.SU, 2010-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://12apr.su/ 'Библиотека по астрономии и космонавтике'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://12apr.su/ 'Библиотека по астрономии и космонавтике'