13. Движение небесных тел под действием сил тяготения

1. Космические скорости и форма орбит

Исходя из наблюдений движения Луны и анализируя законы движения планет, открытые Кеплером, И. Ньютон (1643-1727) установил закон всемирного тяготения. По этому закону, как вы уже знаете из курса физики, все тела во Вселенной притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними:

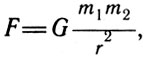
здесь m₁ и m₂ - массы двух тел, r - расстояние между ними, а G - коэффициент пропорциональности, называемый гравитационной постоянной. Его численное значение зависит от единиц, в которых выражены сила, масса и расстояние. Закон всемирного тяготения объясняет движение планет и комет вокруг Солнца, движение спутников вокруг планет, двойных и кратных звезд вокруг их общего центра масс.

Ньютон доказал, что под действием взаимного тяготения тела могут двигаться друг относительно друга по эллипсу (в частности, по кругу), по параболе и по гиперболе. Ньютон установил, что вид орбиты, которую описывает тело, зависит от его скорости в данном месте орбиты (рис. 34).

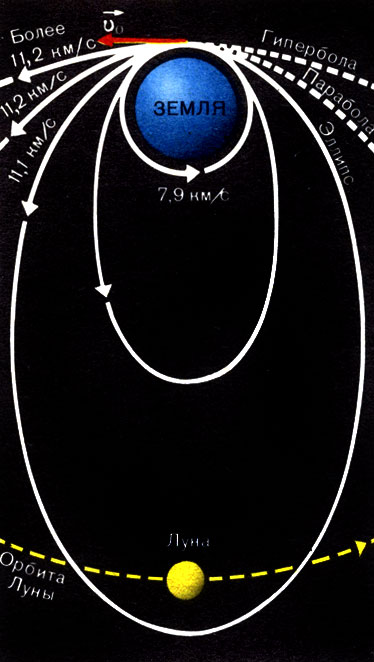
Рис. 34. Зависимость формы орбиты от начальной скорости объекта

При некоторой скорости тело описывает окружность около притягивающего центра. Такую скорость называют первой космической или круговой скоростью, ее сообщают телам, запускаемым в качестве искусственных спутников Земли по круговым орбитам. (Вывод формулы для вычисления первой космической скорости известен из курса физики.) Первая космическая скорость вблизи поверхности Земли составляет около 8 км/с (7,9 км/с).

Если телу сообщить скорость, в 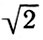раза большую круговой (11,2 км/с), называемую второй космической или параболической скоростью, то тело навсегда удалится от Земли и может стать спутником Солнца. В этом случае движение тела будет происходить по параболе относительно Земли. При еще большей скорости относительно Земли тело полетит по гиперболе. Двигаясь по параболе или гиперболе, тело только однажды огибает Солнце и навсегда удаляется от него.

Средняя скорость движения Земли по орбите 30 км/с. Орбита Земли близка к окружности, следовательно, скорость движения Земли по орбите близка к круговой на расстоянии Земли от Солнца. Параболическая скорость на расстоянии Земли от Солнца равна 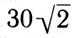км/с≈42 км/с. При такой скорости относительно Солнца тело с орбиты Земли покинет Солнечную систему.

2. Возмущения в движении планет

Законы Кеплера точно соблюдаются только тогда, когда рассматривают движение двух изолированных тел под влиянием их взаимного притяжения. В Солнечной системе планет много, все они не только притягиваются Солнцем, но и притягивают друг друга, поэтому их движения не в точности подчиняются законам Кеплера.

Отклонения от движения, которое происходило бы строго по законам Кеплера, называются возмущениями. В Солнечной системе возмущения невелики, потому что притяжение каждой планеты Солнцем гораздо сильнее притяжения других планет.

Наибольшие возмущения в Солнечной системе вызывает планета Юпитер, которая примерно в 300 раз массивнее Земли. Юпитер оказывает особенно сильное влияние На Движение астероидов и комет, когда они близко к нему подходят. В частности, если направления ускорений кометы, вызванных притяжением Юпитера и Солнца, совпадают, то комета может развить столь большую скорость, что, двигаясь по гиперболе, навсегда уйдет из Солнечной системы. Были случаи, когда притяжение Юпитера сдерживало комету, эксцентриситет ее орбиты становился меньше и резко уменьшался период обращения.

При вычислениях видимого положения планет приходится учитывать возмущения. Теперь делать такие расчеты помогают быстродействующие электронно-вычислительные машины. При запуске искусственных небесных тел и при расчете их траекторий пользуются теорией движения небесных тел, в частности теорией возмущений.

Возможность отправлять автоматические межпланетные станции по желаемым, заранее рассчитанным траекториям, доводить их до цели с учетом возмущений в движении - все это яркие примеры познаваемости законов природы. Небо, которое по представлению верующих является обителью богов, стало ареной человеческой деятельности так же, как и Земля. Религия всегда противопоставляла Землю и небо и объявляла небо недосягаемым. Теперь же среди планет перемещаются искусственные небесные тела, созданные человеком, которыми он может управлять по радио с больших расстояний.

3. Открытие Нептуна

Одним из ярких примеров достижений науки, одним из свидетельств неограниченной познаваемости природы было открытие планеты Нептун путем вычислений - "на кончике пера".

Уран - планета, следующая за Сатурном, который много веков считался самой далекой из планет, была открыта В. Гершелем в конце XVIII в. Уран с трудом виден невооруженным глазом. К 40-м годам XIX в. точные наблюдения показали, что Уран едва заметно уклоняется от того пути, по которому он должен следовать с учетом возмущений со стороны всех известных планет. Таким образом, теория движения небесных тел, столь строгая и точная, подверглась испытанию.

Леверье (во Франции) и Адаме (в Англии) высказали предположение, что, если возмущения со стороны известных планет не объясняют отклонение в движении Урана, значит, на него действует притяжение еще неизвестного тела. Они почти одновременно рассчитали, где за Ураном должно быть неизвестное тело, производящее своим притяжением эти отклонения. Они вычислили орбиту неизвестной планеты, ее массу и указали место на небе, где в данное время должна была находиться неведомая планета. Эта планета и была найдена в телескоп на указанном ими месте в 1846 г. Ее назвали Нептуном. Нептун не виден невооруженным глазом. Так, разногласие между теорией и практикой, казалось, подрывавшее авторитет материалистической науки, привело к ее триумфу.

4. Приливы

Под действием взаимного притяжения частиц тело стремится принять форму шара. Форма Солнца, планет, их спутников и звезд поэтому и близка к шарообразной. Вращение тел (как вы знаете из физических опытов) ведет к их сплющиванию, к сжатию вдоль оси вращения. Поэтому немного сжат у полюсов земной шар, а более всего сжаты быстро вращающиеся Юпитер и Сатурн.

Но форма планет может изменяться и от действия сил их взаимного притяжения. Шарообразное тело (планета) движется в целом под действием гравитационного притяжения другого тела так, как если бы вся сила притяжения была приложена к ее центру. Однако отдельные части планеты находятся на разном расстоянии от притягивающего тела, поэтому гравитационное ускорение в них также различно, что и приводит к возникновению сил, стремящихся деформировать планету. Разность ускорений, вызываемых притяжением другого тела, в данной точке и в центре планеты называется приливным ускорением.

Рассмотрим для примера систему Земля - Луна. Один и тот же элемент массы в центре Земли будет притягиваться Луной слабее, чем на стороне, обращенной к Луне, и сильнее, чем на противоположной стороне. В результате Земля, и в первую очередь водная оболочка Земли, слегка вытягивается в обе стороны вдоль линии, соединяющей ее с Луной. На рисунке 35 океан для наглядности изображен покрывающим всю Землю. В точках, лежащих на линии Земля - Луна, уровень воды выше всего - там приливы. Вдоль круга, плоскость которого перпендикулярна направлению линии Земля - Луна и проходит через центр Земли, уровень воды ниже всего - там отлив. При суточном вращении Земли в полосу приливов и отливов поочередно вступают разные места Земли. Легко понять, что за сутки могут быть два прилива и два отлива.

Солнце также вызывает на Земле приливы и отливы, но из-за большой удаленности Солнца они меньше, чем лунные, и менее заметны.

С приливами перемещается огромная масса воды. В настоящее время приступают к использованию громадной энергии воды, участвующей в приливах, на берегах океанов и открытых морей.

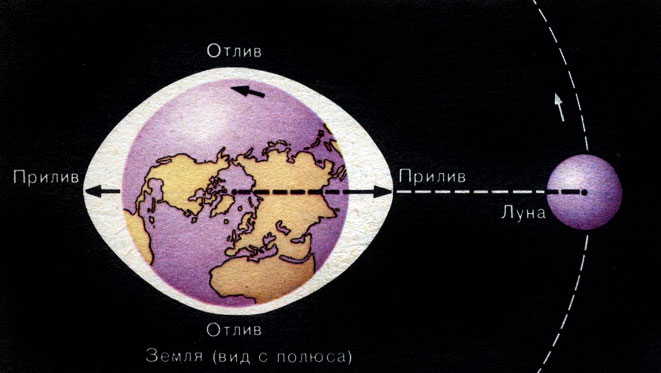
Рис. 35. Схема лунных приливов

Ось приливных выступов должна быть всегда направлена к Луне. При вращении Земля стремится повернуть водяной приливный выступ. Поскольку Земля вращается вокруг оси гораздо быстрее, чем Луна обращается вокруг Земли, то Луна оттягивает водяной горб к себе. Происходит трение между водой и твердым дном океана. В результате возникает так называемое приливное трение. Оно тормозит вращение Земли, и сутки с течением времени становятся длиннее (когда-то они составляли только 5-6 ч). Сильные приливы, вызываемые на Меркурии и Венере Солнцем, по-видимому, и явились причиной их крайне медленного вращения вокруг оси. Приливы, вызываемые Землей, настолько затормозили вращение Луны, что она всегда обращена к Земле одной стороной. Таким образом, приливы являются важным фактором эволюции небесных тел и Земли.

5. Масса и плотность Земли

Закон всемирного тяготения позволяет также определить одну из важнейших характеристик небесных тел - массу, в частности массу нашей планеты. Действительно, исходя из закона всемирного тяготения, ускорение свободного падения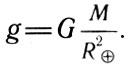

Следовательно, если известны значения ускорения свободного падения, гравитационной постоянной и радиуса Земли, то можно определить ее массу.

Подставив в указанную формулу значение g = 9,8 м/с², G = 6,67*10^-11 Н*м²/кг², R=6370 км, найдем, что масса Земли М=6*10²⁴ кг.

Зная массу и объем Земли, можно вычислить ее среднюю плотность. Она равна 5,5*10³ кг/м³. Но плотность Земли с глубиной возрастает, и, по расчетам, вблизи центра, в ядре Земли, она равна 1,1*10⁴ кг/м³. Рост плотности с глубиной происходит за счет увеличения содержания тяжелых элементов, а также за счет увеличения давления.

(С внутренним строением Земли, изучаемым астрономическими и геофизическими методами, вы знакомились в курсе физической географии.)

Упражнение 12

1. Чему равна плотность Луны, если ее масса в 81 раз, а радиус в 4 раза меньше, чем у Земли?

2. Чему равна масса Земли, если угловая скорость Луны 13,2° в сутки, а среднее расстояние до нее 380 000 км?

6. Определение масс небесных тел

Ньютон доказал, что более точная формула третьего закона Кеплера такова:

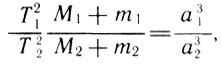
где M₁ и М₂ - массы каких-либо небесных тел, a m₁ и m₂ - соответственно массы их спутников. Так, планеты считаются спутниками Солнца. Мы видим, что уточненная формула этого закона отличается от приближенной наличием множителя, содержащего массы. Если под M₁=M₂=Mпонимать массу Солнца, а под m₁ и m₂ - массы двух разных планет, то отношение 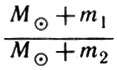будет мало отличаться от единицы, так как m₁ и m₂ очень малы по сравнению с массой Солнца. При этом точная формула не будет заметно отличаться от приближенной.

Уточненный третий закон Кеплера позволяет определить массы планет, имеющих спутников, и массу Солнца. Чтобы определить массу Солнца, будем сравнивать движение Луны вокруг Земли с движением Земли вокруг Солнца:

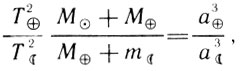
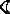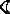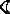где Ти а- период обращения Земли (год) и большая полуось ее орбиты, Tи а - период обращения Луны вокруг Земли и большая полуось ее орбиты, М - масса Солнца, М - масса Земли, m -масса Луны. Масса Земли ничтожна по сравнению с массой Солнца, а масса Луны мала (1:81) по сравнению с массой Земли. Поэтому вторые слагаемые в суммах можно отбросить, не делая большой ошибки. Решив уравнение относительно 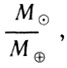имеем:

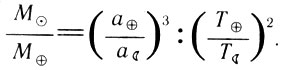
Эта формула позволяет определить массу Солнца, выраженную в массах Земли. Она составляет около 333 000 масс Земли.

Для сравнения масс Земли и другой планеты, например Юпитера, надо в исходной формуле индекс 1 отнести к движению Луны вокруг Земли массой M₁, a 2 - к движению любого спутника вокруг Юпитера массой М₂.

Массы планет, не имеющих спутников, определяют по тем возмущениям, которые они своим притяжением производят в движении соседних с ними планет, а также в движении комет, астероидов или космических аппаратов.

Упражнение 13

1. Определите массу Юпитера сравнением системы Юпитера со спутником с системой Земля - Луна, если первый спутник Юпитера отстоит от него на 422 000 км и имеет период обращения 1,77 сут. Данные для Луны должны быть вам известны.

2. Вычислите, на каком расстоянии от Земли на линии Земля - Луна находятся те точки, в которых притяжения Землей и Луной одинаковы, зная, что расстояние между Луной и Землей равно 60 радиусам Земли, а масса Земли в 81 раз больше массы Луны.