
Кеплера законы
Изучая результаты многолетних наблюдений планеты Марс датским астрономом Т. Браге, немецкий ученый И. Кеплер обнаружил, что орбита Марса не окружность, а имеет вытянутую форму эллипса. Как известно, у эллипса есть две точки F1 и F2 (рис. 1), сумма расстояний которых (r1 + r2) от любой точки В эллипса есть величина постоянная. Прямая А1А2, лежащая внутри эллипса и проходящая через его фокусы, называется большой осью эллипса. Мерой сплюснутости эллипса является его эксцентриситет, равный отношению расстояния между фокусами к большой оси e = F1F2/А1А2. Линия, соединяющая любую точку эллипса с одним из его фокусов, называется радиусом-вектором этой точки.
Кеплер исследовал движения всех известных в то время планет и вывел три закона движения планет.
Во-первых, орбиты всех планет (а не только Марса) являются эллипсами с общим фокусом, в котором находится Солнце. Степень вытянутости орбит у разных планет различная. У Земли эксцентриситет очень мал (всего 0,017), и орбита Земли мало отличается от окружности. Поэтому кратчайшее расстояние Земли от Солнца (в перигелии) мало отличается от наибольшего (в афелии). Наиболее вытянутые орбиты имеют Меркурий (эксцентриситет 0,21) и Плутон (эксцентриситет 0,25).
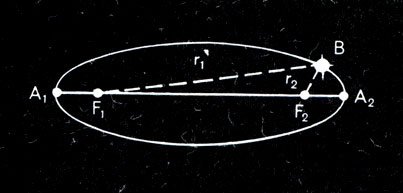
Рис. 1. Орбиты планет имеют форму эллипса
Во-вторых, каждая планета по своей, орбите движется таким образом, что ее радиус-вектор за одинаковые промежутки времени описывает равные площади (площади секторов A1A2F и B1B2F на рис. 2 равны). Это значит, что чем ближе планета к Солнцу, тем у нее больше скорость движения по орбите. Например, Марс вблизи перигелия движется со скоростью 26,5 км/с, а около афелия его скорость уменьшается до 22 км/с. Кометы, являясь членами Солнечной системы, движутся по тем же законам, что и планеты, но у некоторых из них орбиты настолько вытянуты, что вблизи Солнца скорость их движения доходит до 500 км/с, а в афелии их скорость снижается до 1 см/с.
Первые два закона движения планет Солнечной системы Кеплер опубликовал в 1609 г. Спустя десять лет он обнаружил третью закономерность в движении планет и сформулировал ее так: отношение кубов больших полуосей орбит двух любых планет Солнечной системы равно отношению квадратов периодов их обращения вокруг Солнца. Этот закон имел большое значение для определения масштабов Солнечной системы, т. е. расстояний планет от Солнца. Если за единицу времени принять один год, а за единицу расстояния - среднее расстояние Земли от Солнца (астрономическую единицу), то, определив из наблюдений период обращения какой-либо планеты в годах (Т), легко получить значение большой полуоси этой планеты (а) по формуле
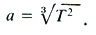
Например, период обращения Марса по наблюдениям равен 1,88 года. Тогда по этой формуле можно вычислить большую полуось орбиты Марса, которая оказывается равной 1,52 а. е. Таким образом, Марс примерно в полтора раза дальше от Солнца, чем Земля.
Установленные Кеплером законы движения планет еще раз наглядно показывают, что мир планет есть стройная система, управляемая единой силой, источником которой является Солнце.
|
ПОИСК:
|
© 12APR.SU, 2010-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://12apr.su/ 'Библиотека по астрономии и космонавтике'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://12apr.su/ 'Библиотека по астрономии и космонавтике'