Ура! Да здравствует контакт! (Окончание спора)

О. Предположим, цивилизация X и цивилизация Y пытаются установить контакт. Как ты думаешь, можно вычислить потребную мощность передатчика?

П. Она же зависит от многих величин, которые мы будем высасывать из пальца!

О. Вынь палец изо рта. Попробуем логически моделировать эту систему связи, опираясь на теорию и практику землян.

П. Но ведь у них техника...

О. Перестань. Техника другая, но законы, понимаешь, ЗА-КО-НЫ те же. Скажи мне, от чего зависит предельная дальность радиосвязи?

Рис. 50

П. Попытаюсь вспомнить. От мощности передатчика P - раз. От диаметров передающей и приемной антенны D₁ и D₂ - два. От температуры шумов на входе приемника T - три. От рабочей длины волны (она определяет уровень внешних помех) - четыре... Вот, кажется, и все.

О. Слона-то ты и не приметил. Хочешь, посылай 1000 телеграмм в час, хочешь, посылай одну в сутки - нужна та же мощность, так?

П. Нет, конечно. Чем больше скорость работы, тем полоса пропускания приемника Δt должна быть шире, тем больше он вбирает в себя шумов, тем больше нужна мощность передатчика, чтобы их перекричать.

О. Верно. Но это не все. Дальность еще зависит от того, насколько нам надо перекричать шум. А это, в свою очередь, определяется способом погрузки информации на переносчик. Ведь нам надо выиграть поединок на входе приемника (см. рисунки). Чем способ передачи помехоустойчивей, тем меньшую мощность надо для победы.

П. Конечно.

О. Итак, цивилизация X отстоит от цивилизации на расстоянии Y световых лет. Подсчитай, пожалуйста, какая нужна мощность для радиосвязи.

П. Но у меня же нет ни единой цифры.

О. Держу пари, что все необходимые цифры лежат в твоем затянувшемся паутиной пессимизма "запоминающем устройстве", то бишь - голове. На какой волне меньше всего шумы Галактики?

П. Они достигают минимума приблизительно при волнах от 3 до 30 сантиметров.

О. Верно. Какой диаметр антенн достигнут в этом диапазоне?

П. Порядка сотни метров.

О. Убедился? Ты все отлично знаешь. Дальше действуй сам. Встряхни свою память. Ведь там уйма сведений валяется без дела. Вот логарифмическая линейка, бумага. А я пока полистаю свежие журналы. Да попутно оцени, сколько звезд находится в сфере радиуса R, считая, что плотность звезд в сфере такая же, как в окрестности солнечной системы.

П. Готово. Вот расчетная формула и результаты.

О. Как же ты их получил?

П. Я считал, что обе цивилизации находятся на уровне, близком к нашему. Поэтому можно принять: диаметр антенны D=150 метров, длина волны λ=10 сантиметров, температура шумов T=10°K, минимальное отношение мощностей сигнал/шум N=10.

О. А полоса пропускания приемника?

П. Я ее принял равной 10 герцам.

О. Что же это за сигнал?

П. Это либо непрерывное излучение синусоидального переносчика без всякой модуляции, либо с очень медленной модуляцией - несколько посылок в секунду.

О. Какая же нужна мощность?

П. Ближним звездам - десятки киловатт, дальним - миллионы киловатт.

О. Ну вот видишь, ты сам себе доказал, что уже сегодня мы можем прокричать "ау!" ближайшей сотне звезд. Передатчики такой мощности - это уже достижимая почти величина в нашем диапазоне волн.

П. "Ау!"-то, может? и можем, но как быть с посылкой более содержательной информации?

О. А что?

П. Будем говорить о передаче дискретных двоичных сигналов. Весьма вероятно, что именно этот гибкий помехоустойчивый метод будет использоваться. Так вот, если мы захотим увеличить скорость передачи в 100 раз по отношению к принятой в расчете, то нам нужно в 100 раз увеличить мощность передатчика. А ведь 100 посылок в секунду на нашей планете - это телеграфная линия средней скорости. Как же быть с идеей Кардашева?

О. Во-первых, у нас есть еще резервы. Например, ты слышал об уникальной антенне в Пуэрто-Рико? Ее диаметр 300 метров. Использование антенн такого типа может дать заметное снижение необходимой мощности. Далее, мы можем в несколько раз снизить величину N; применяя фазовое телеграфирование и коды, корректирующие ошибки. Во-вторых, можно сложить мощности нескольких передатчиков в эфире...

П. Все равно мы не сможем создать передающее устройство, которое "выплюнет" все достижения нашей цивилизации за короткий отрезок времени. Не хватит пороху!

О. Что ты называешь коротким?

П. Скажем, дни или недели. Нельзя же вбирать эту информацию годами или десятками лет!

О. Да, пожалуй.

П. Вот видишь. Так есть ли надежда?

О. Стоп! Ведь мы с тобой условно считали, что X и Y цивилизации типа земной. Но если мы X, то Y могла уйти далеко вперед! Это может быть даже сверхцивилизация, владеющая сказочными энергетическими ресурсами!

П. Ну и что?

О. А то, что в уравнение связи входит произведение технических возможностей X и Y. Это значит, что мы уже можем принимать не только простейшие сигналы типа "ау!", но и богатейший поток информации от таких цивилизаций.

П. Ты обещал цифры.

О. Пожалуйста. Воспользуемся расчетами Н. Кардашева. Возьмем самый крайний случай. Сверхцивилизация Y решила передать нам, темным иксам, гигантский поток информации объемом, приблизительно равным содержанию всех книг, изданных за время существования человечества. Их число равно 10⁸. Будем считать, что при преобразовании содержащейся в каждой из книг информации в двоичную в среднем потребуется 10⁶ двоичных единиц. Можно всю эту премудрость передать за одни сутки?

П. Никогда!

О. Нет, ты посчитай.

П. Попробую. Значит, общее число посылок Да - Нет за сутки составит 10⁶×10⁸=10¹⁴. В сутках 105 секунд. Следовательно, в секунду надо передать 10¹⁴×10^-5=10⁹. То есть в секунду надо прокричать Да - Нет тысячу миллионов раз! Не сорвут ли игреки горло и позволят ли это те общие законы природы, на которых ты так настаивал?

О. Да не бойся ты великанов цифр. Считай дальше. Какое нужно приемнику "горло", чтобы испить всю эту информацию сполна?

П. Можно считать, что полоса пропускания приемника численно равна числу посылок в секунду. Следовательно, нужен приемник с неслыханной полосой пропускания Δf=1000 мегагерц!

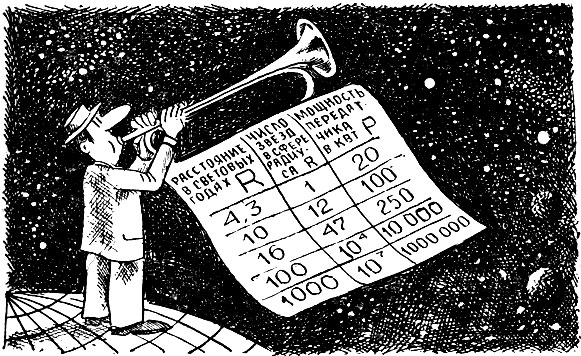
Рис. 51

О. Может, ты теперь назовешь законы, которые препятствуют "...выдумать порох непромокаемый" и создать приемник с таким прожорливым горлом?

П. Нет. Но...

О. Но мы же хватили через край. В этом лесу из 10¹⁴Да - Нет запутается, наверное, любая сверхцивилизация. Тут неимоверная избыточность. Фактически нужно передавать в миллионы раз меньшую информацию.

П. Все равно потребуются титанические мощности.

О. "А это пожалуйста!" - ответят тебе сверхцивилизации. Расчеты показывают, что цивилизации II и III типа могут не только аукать на всю Метагалактику, но и легко передать основные свои тайны многим юным или медленно развивающимся цивилизациям. Если, конечно, они покинут болото сомнений и соорудят хотя бы примитивную свою "приемную" половину радиомоста в космическую бездну.

Рис. 52

Ну хватит терять время. Идешь в группу? Выдай только одну двоичную единицу информации - Да или Нет? К черту всякую избыточность!

П. Да. Но...

О. Я же просил только одну двоичную единицу.

П. Это "но" относится уже к задаче, которую ты мне поставишь.

О. Тогда другое дело!

П. Я ведь всегда больше тяготел к абстракции. Разумной, конечно. Я больше люблю Врубеля, чем, скажем, Пикассо. Одно время я, как буриданов осел, долго стоял между математикой и физикой. Потом отведал того и другого и вернулся к математической куче.

О. Вот и отлично! Нам нужно создать математическую модель хотя бы двух цивилизаций, тех самых X и Y, которые упорно ищут друг друга.

П. Но...

О. За следующее "но" ты будешь избит, и не математически, а чисто физически.

П. Молчу. Буду давить их в себе, как чертят-помех.

О. Ты создашь первую модель такого поиска. Представь игру двух вычислительных машин.

П. В карты?

О. Ну и остряк! Наша игра в тысячу раз интересней! Машины изолированы друг от друга. Единственная связь - через эквивалент межзвездной среды.

П. Математический?

О. Он может быть и математическим и физическим. Это не принципиально.

П. Ну и что?

О. Одна, скажем, излучает сигналы в среду! Зовет. Меняет волны, меняет направления, изменяет временную и частотную избыточность, способы передачи. Шлет сигналы обучения своей азбуке, информацию...

П. А X в это время...

О. Подожди. В межзвездных просторах сигнал слабеет, худеет. Да еще черти примешивают к нему свое вредное зелье - помехи. Вот это и получает машина X.

П. Ее задача - разыскать разумный сигнал, принять и запомнить его, обучиться его азбуке, разгадать переданную "клинопись" и выдать ее нам, так?

О. Именно так.

Рис. 53

П. А дальше?

О. Дальше сличаем поданную космическую телеграмму с принятой. Ставя X и Y в разные условия, проигрываем сотни вариантов и все ближе и ближе подходим к раскрытию тайны...

П. Все понял.

О. Берешься?

П. Да.

Как следует из полемики оптимиста и пессимиста, мы с вами, читатель, принадлежим отнюдь не к суперцивилизации, поэтому должны пока больше внимания уделять приему информации от цивилизаций, ушедших вперед. В следующей главе речь пойдет о поиске сигналов в наших земных условиях.