§ 53. Визуальные наблюдения метеоров. Определение радиантов

Радиантом называется та точка небесной сферы, из которой летел данный метеор. Если бы метеор летел точно на наблюдателя, то он вспыхнул бы на небе яркой точкой, находящейся в радианте. При идеально точных наблюдениях траекторий метеора, видимых из двух достаточно удаленных пунктов (корреспондирующих наблюдениях), можно определить радиант отдельно взятого метеора. При наблюдениях же, выполняемых из одного пункта, определить радиант одного метеора нельзя. В таком случае при изучении метеорных потоков пользуется другим их свойством. Потоковые метеоры можно считать движущимися в пространстве параллельно друг другу. Вследствие влияния перспективы мы будем видеть их расходящимися из одной точки - радианта Р, как это показано на рис. 112. В этом случае наблюдатель подобен человеку, стоящему между параллельными рельсами на полотне железной дороги: он видит, что рельсы как бы сходятся в одной точке на горизонте.

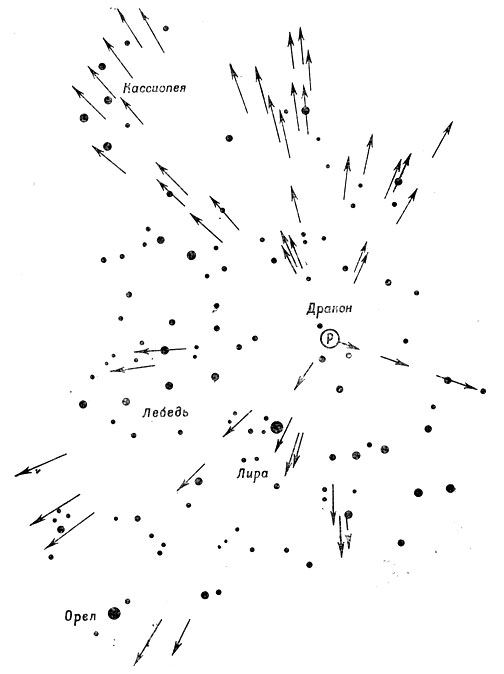
Рис. 112. Поток Драконид в 1933 г. Буквой Р в кружке обозначен радиант потока

Для определения положения радианта метеорного потока надо возможно точнее нанести на звездную карту пути метеоров и продолжить их в обратном направлении до взаимного пересечения.

Что нужно сделать, чтобы хорошо подготовиться к наблюдениям? На основании многолетних метеорных исследований известно, в какой области звездного неба и в какое время будут наблюдаться метеорные потоки. Краткие сведения об обильных метеорных потоках приведены в таблице 8 (стр. 377). Зная положение радианта, наблюдатель выбирает из звездного атласа нужную карту неба, на которую он будет наносить наблюдавшиеся им пути метеоров.

Наблюдать метеоры стоя утомительно. Лежа наблюдать неудобно, так как придется наносить пути метеоров на карту и записывать сведения о них в журнал наблюдений. Поэтому рекомендуется запастись откидным креслом с натянутой на нем парусиной и столиком, на котором расположить карту, журнал, электрический фонарик, часы и линейку. Теперь наблюдатель, поудобнее расположившись в кресле и избрав определенную область неба для патрулирования, начинает возможно внимательнее следить за пей. При этом он должен осматривать всю избранную область, а не фиксировать внимание на какой-либо звезде. Заметив полет метеора, наблюдатель старается как можно точнее отметить те точки, в которых метеор появился и затем угас. Для этого он может воспользоваться линейкой: достаточно поднять линейку над головой и спроектировать ее (по памяти) вдоль траектории пролетевшего метеора. Тогда будет легче отметить, где на фоне звездного неба начался путь метеора и где он окончился. Отыскав соответствующие положения этих точек на звездной карте, наносим их и соединяем по линейке прямой линией. Стрелкой указываем направление полета метеора и рядом пишем порядковый номер. Под тем же номером заносим в журнал наблюдений данные о пролетевшем метеоре: время полета (с точностью до минуты), видимую звездную величину (которую оцениваем по памяти сравнением с соседними звездами), продолжительность полета и цвет метеора.

Из сказанного очевидно, что наблюдатель метеоров, прежде чем приступить к наблюдениям, должен хорошо изучить наблюдаемую область звездного неба и знать не только названия звезд, но и их звездные величины. Данные о звездах он может найти в «Справочнике любителя астрономии» П. Г. Куликовского, о чем мы уже не раз упоминали.

Кроме того, надо заметить, что свет фонарика не должен быть ярким, чтобы не утомлять глаз наблюдателя, чтобы сразу же после записи наблюдений он мог видеть слабые звезды.

На следующий день после наблюдений проводится их первичная обработка. Наложив на звездную карту прозрачную координатную сетку (кругов склонений и суточных параллелей), отсчитываем экваториальные координаты начала и конца пути каждого метеора; их также записываем в журнал.

К сожалению, отыскивать радиант на обычной карте звездного неба нельзя, как так она построена в неподходящий для этой цели проекции. Истинная траектория метеора с большой точностью прямолинейна. Поэтому видимые траектории метеоров - это дуги больших кругов небесной сферы, которые на обычных картах звездного неба могут не оказаться прямыми линиями. Нанесенный на такую карту путь метеора изображен прямой линией чисто условно и потому особую роль играют координаты точек начала и конца пути.

Путь метеора будет прямолинейным лишь на карте, построенной в так называемой гномонической проекции. Это - проекция небесной сферы на плоскость Н, касающуюся небесной сферы в некоторой избранной нами точке М_о (рис. 113). В самом деле, если взять две точки, М₁ и М₂, на одном большом круге небесной сферы и построить из ее центра лучи ОМ₁ и ОМ₂, то через них пройдет плоскость М₁ОМ₂ и все точки дуги большого круга M₁M₂ будут лежать в этой плоскости, которая пересекает плоскость Я по прямой линии Т₁Т₂.

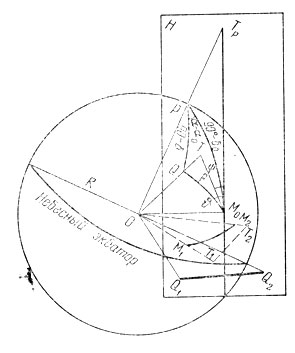
Рис. 113. К объяснению гномонической проекции

Поскольку все круги склонений - большие круги небесной сферы, проходящие через полюс мира Р, на гномонической сетке они изобразятся прямыми линиями, проходящими через точку

Тр, в которой луч ОР пересекает плоскость Я.

Иначе изображается суточная параллель. Только одна из суточных параллелей - небесный экватор - является дугой большого круга и потому изображается прямой линией Q₁Q₂. Остальные суточные параллели, как показывают расчеты, должны изображаться эллипсами и гиперболами, а одна из них - параболой. Получается сетка, изображенная на рис. 114. На этом рисунке мы видим две взаимно перпендикулярные оси координат М_оХ и M_оY. В начале координат М_о плоскость проекций касается небесной сферы. Мы выбрали при построении сетки точку М0 так, чтобы ее часовой угол t_о был равен нулю, а склонение δ_о = 30°. Идущие от точки ТР по радиусам прямые линии - это изображения кругов склонений. Их часовые углы t указаны около окончания каждой из прямых на нижней, левой и верхней частях рамки от t = 0° до t - 180° через каждые 10°. Суточные параллели, как было сказано, изображаются дугами (кроме небесного экватора). Справа от каждой дуги указано соответствующее склонение, от - 20 до +90°, также через 10°. Можно сделать сетку и более густой - через 5°, но тогда ее надо рисовать в большем масштабе. Зная координаты любой точки t и δ, можно найти по этим линиям (интерполируя между ними) ее положение.

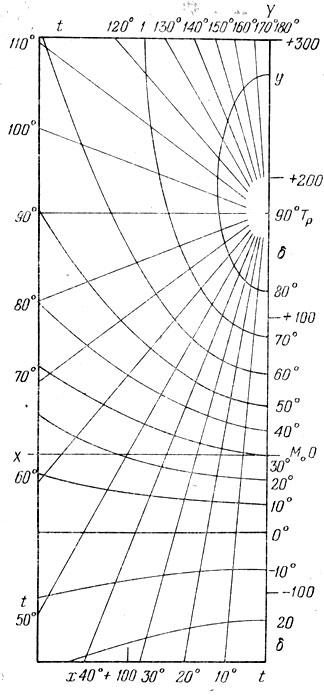
Рис. 114. Гномонисечкая координатная сетка

Для пользования сеткой нет необходимости вычислять часовые углы. Если приписать точке М_о любое прямое восхождение α_о, то прямые восхождения кругов склонений будут равны α_о + 10°, α_о + 20°, α_о + 30° и т. д. На рисунке 114 для наглядности изображена только левая часть сетки; правая, ненарисованная часть симметрична относительно оси М_оУ.

На оси координат М_оY и на нижней рамке помечены также отрезки числами -100, 0, +100, +200, +300. Они указывают масштаб прямоугольных координат х и у. Наблюдатель при желании может построить достаточно крупномасштабную сетку, пользуясь таблицей 10 (стр. 378), где указаны координаты х и у для большой совокупности равноотстоящих значений t и δ.

Выше мы указали, что черновая обработка наблюдений заканчивается определением экваториальных координат точек начала (α₁, δ₁) и конца (α₂, δ₂) пути метеора. Теперь мы можем нанести эти точки на гномоническую сетку и соединить их прямой линией со стрелкой в конце пути. Полученные для всех метеоров прямолинейные пути необходимо продолжить в обратном направлении. Эти пути должны выходить из одной точки - метеорного радианта.

Если бы наблюдения были безошибочными и все метеоры двигались бы по строго параллельным путям, то все их траектории, продолженные в обратном полету направлении, должны были бы пересечься в одной точке и оставалось бы только определить ее координаты. Однако на практике получается несколько иначе пути всех метеоров, принадлежащих одному потоку, не пересекаются в одной точке, а выходят из небольшой площадки, которую называют площадью радиации. Радиант находится где-то внутри этой площадки.

Считается, что радиант существует и метеоры принадлежат одному потоку, если соблюдены следующие условия:

1. Если не менее четырех метеоров, наблюдавшихся в течение одной ночи, имеют пути, пересекающиеся внутри круга с диаметром в 2°.

2. Если три метеора, наблюдавшиеся в течение одной ночи, и два метеора, наблюдавшиеся в следующую ночь, удовлетворяют тому же условию.

3. Может случиться, что метеор летел прямо на наблюдателя и последний видел его как яркую вспыхнувшую точку. Такой метеор называется стационарным. Его положение на небе определяет радиант, без всяких построений.

Если наблюдения, произведенные в течение одной ночи, дают не один радиант, а несколько, то это означает, что в данную ночь действовало несколько потоков.

Графический способ обработки наблюдений, конечно, прост, но оставляет у требовательного наблюдателя чувство неудовлетворенности, так как единого ответа не получается, и площадь радиации можно трактовать несколько произвольно. Если наблюдатель не пожалеет времени для выполнения довольно кропотливых вычислительных работ, то он может решить задачу гораздо определеннее и даже оценить точность полученных результатов.

Для этого надо сначала решить несколько простых задач.