§ 54. Четыре простые задачи

Пусть на небесной сфере заданы положения двух точек их экваториальными координатами: М₁(α₁, δ₁) и М₂(α₂, δ₂)

Задача 1. Определить угол между лучами зрения ОМ₁ и ОМ₂, что равноценно определению длины дуги большого круга небесной сферы, проходящего через точки М₁ и М₂.

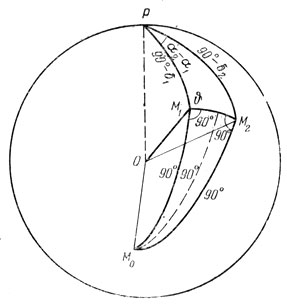
Рис. 115. К решению задач

Для решения этой задачи рассмотрим сферический треугольник, образованный на небесной сфере точками М₁, М₂ и полюсом мира Р (рис. 115). Его стороны равны:

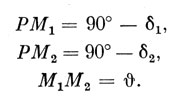
Угол при точке Р равен разности прямых восхождений: ∠Р = α₂ - α₁. Применяя к стороне М₁М2 формулу косинуса стороны, находим

cos υ = cos (90° - δ₁) cos (90° - δ₂) + sin (90° - δ₁) sin (90° - δ₂) cos (α₂ - α₁) или

cos υ = sinδ₁ sin δ₂ + cos δ₁ cos δ₂ [cosα₁ cos α₂ + sin α₁ sin α₂]. (5.1)

Задача 2. Задано положение точки М₁. Найти, какому условию удовлетворяет точка М_о, которая удалена на небесной сфере от точки М₁ на угол, равный 90°.

В формуле (5.1) полагаем υ=90°, так что cos υ=0 и δ₂=δ_о; тогда

cos δ₁ cosα₁ cosδ_о cos α_о + cosδ₁ sinα₁ cosδ_о sinα_о = - sinδ₁ sinδ_о. (5.2) Введем обозначения:

Х=ctgδ_ocosα_o и Y=ctgδ_osinα_o (5.3)

Тогда условие (5.2) перепишется в виде

Xcosδ₁cos α₁ + Ycosδ₁sinα₁=-sinδ₁ (5.4)

Мы получили одно уравнение с двумя неизвестными X, Y, так что это условие положения искомой точки М_о не определяет. Так и должно быть, так как вокруг точки М₁ можно описать большой круг, все точки которого удалены от нее на 90°. Такой большой круг называется экватором точки М₁.

Задача 3. Даны две точки, М₁ и M₂, Найти такую точку небесной сферы М_о, которая была бы удалена от двух заданных точек на 90°.

Для решения этой задачи надо написать два уравнения (5.4) и решить их совместно. Мы получаем систему

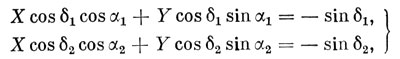
(5.5)

решение которой имеет вид

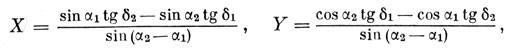
(5.6)

в чем нетрудно убедиться, выполнив несложные вычисления.

Из условия (5.3) можно получить формулы, определяющие координаты точки М_о:

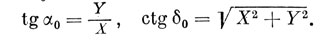
(5.7)

Точка М_о называется полюсом дуги большого круга М₁М₂ и обладает интересными свойствами.

Во-первых, она удалена на 90° не только от точек М₁ и М₂, но и от любой точки, находящейся на большом круге, проходящем через М¹ и М₂. Таким образом, зная X и Y из заданных координат точек М₁ и М₂, мы определяем уравнение большого круга, проходящего через эти точки:

Xcosδcosα+Ycosδsinα=-sinδ, (5.8)

где а и б - переменные координаты любой точки, лежащей на большом круге - экваторе, называемые текущими координатами.

Во-вторых, если соединить точку М0 с любой точкой ее экватора дугой большого круга, то мы получим при их пересечении угол, равный 90°. Это видно из рис. 115.

Приложение этой задачи к метеорной астрономии очевидно. Так как метеор летит по дуге большого круга, то траектория метеора определяется точкой М₀ - «полюсом» метеора. Для каждого метеора можно определить свои значения X и Y по формулам (5.6).

Задача 4. Через точки М₁ и М₂ проведена дуга большого круга, определяемого положением его полюса М₀. Найти «сферическое расстояние» точки Ms от этого круга (рис. 116).

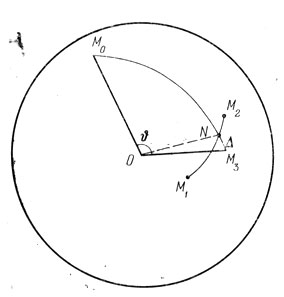
Рис. 116. К определению 'сферического расстояния'

Прежде всего надо определить понятие «сферическое расстояние». Для этого проведем через точку М₃ дугу М₃М₀ большого круга, перпендикулярную к большому кругу М₁М₂. Согласно последнему свойству точки М0 этот новый большой круг должен пройти через точки М₃ и М₀.

Тогда под «сферическим расстоянием» мы будем понимать угол Δ, заключенный между направлениями ОМ₃ и ON. Очевидно, что Δ = υ - 90°, где υ - угол между направлениями ОМ₀ и ОМ₃.

Найдем sin Δ = sin (Δ - 90°) = - sin (90°- Δ) = - cos Δ , после чего воспользуемся формулой (5.1) и получим

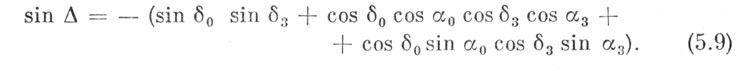
Мы вывели основные формулы, которые позволят нам решить ряд задач метеорной астрономии.