§ 61. Метеорные следы

Во время полета через атмосферу метеорное тело вызывает в ней хотя и кратковременные, но значительные изменения. Вдоль всего пути метеорного тела остается насыщенный электронами «метеорный» ионизационный столб. Он постепенно рассеивается - диффундирует в окружающее невозмущенное метеором пространство.

Ионизационный столб способен рассеивать радиоволны, и открытие этого его свойства привело к возникновению новой отрасли науки - метеорной радиолокационной астрономии. Направляя в атмосферу радиоимпульсы, астрономы регистрируют их отражение от метеорных столбов в тех случаях, когда эти столбы возникают. Появилась возможность обнаруживать и наблюдать метеорные явления в любое время суток, в любую погоду, даже сквозь облака.

Постепенное совершенствование методов метеорной радиоастрономии позволило регистрировать появление таких метеоров, которые из-за своего малого блеска не видны даже в телескоп. Систематически изучается метеорная активность и ее зависимость от времени года и изменение в течение суток. Оцениваются массы метеоров и вычисляются их орбиты. Ввиду же того, что метеор образуется не мгновенно, а пролетает через атмосферу в течение некоторого времени, отраженный сигнал «формируется» постепенно, и это дает возможность по изучению его формы определить скорость движения метеора.

И, наконец, радиолокационные наблюдения дают возможность определять скорость и направление ветра, сносящего метеорный столб в сторону. Более того, разработаны методы практического использования отражений от электронного столба, для обеспечения дальней направленной радиосвязи.

Существуют также устойчивые метеорные следы, образующиеся после полета яркого метеора (далеко не каждого), которые видны более или менее длительное время, по крайней мере в течение нескольких минут. За это время метеорный след постепенно ослабляет свою яркость, в нём появляются отдельные сгущения, и пока никто не знает, как и по какому закону происходит это падение яркости.

Практика показала, что видимый невооруженным глазом след не всегда оказывается устойчивым и почти мгновенно рассеивается. С другой стороны, бывает и так, что устойчивый след виден в бинокль или телескоп, в то время как невооруженным глазом он вообще не был замечен. Таким образом, тем, кто интересуется наблюдениями устойчивых метеорных следов, рекомендуется просматривать конец траектории каждого яркого метеора в бинокль или в телескоп, обладающий достаточно большим полем зрения.

Явление протекает примерно так. В первые секунды существования устойчивого следа он выглядит в виде серебристой полосы длиной примерно в 3-4°. В течение 3-4 секунд эта полоса остается неподвижной, а затем начинает смещаться на фоне звездного неба, покрывая встретившиеся на пути звезды. Полезно отмечать, с точностью до секунды, моменты покрытия отдельных звезд. В средней продольной части следа иногда наблюдается параллельная его краям темная «трубка».

Особо ценны двусторонние, корреспондирующие наблюдения устойчивого метеорного следа, но таких пока очень мало. Вряд ли можно производить такие наблюдения визуально по следующей причине. Когда след начнет распадаться на отдельные сгущения, два удаленных друг от друга наблюдателя не смогут выделить одно и то же сгущение и следить за его перемещением, даже если бы они могли связываться друг с другом по радиотелефону. А наблюдения за перемещениями двух разных деталей следа из двух пунктов никаких данных об их истинных движениях не дадут.

Даже фотографические наблюдения наиболее ярких следов для получения надежных результатов должны быть синхронными.

Вообще говоря, «ловцам» метеорных следов можно рекомендовать такую технику фотографических наблюдений. К телескопу нужно прикрепить светосильную камеру так, чтобы их оптические оси были параллельны. Найдя след и выделив в нем какую-либо деталь, надо производить экспозиции длительностью около 10 - 15 секунд, гидируя инструмент по движению выбранной детали, т. е. перемещая телескоп так, чтобы деталь все время была в центре поля зрения телескопа. При этом желательно, чтобы наблюдатель, расположенный во втором пункте наблюдений, также организовал свои фотографические наблюдения, делая перерывы в экспозициях через заранее условленное время.

Сравнение снимков между собой даст возможность отыскать при обработке наблюдений соответстьшнные точки па обоих изображениях. При обработке этих наблюдений применяются те же самые формулы, которые приведены в § 60, с тем отличием, что координаты соответственных точек нельзя будет искать из уравнений больших кругов, как это было в случае измерения и обработки корреспондирующих снимков метеоров.

Как же поступить в данном случае. Лучшее, что можно рекомендовать,- это использование гномонической координатной сетки. Дело в том, что изображения следа не резки и точных измерений координат сделать вообще нельзя. Обрабатывая такие снимки, автор проектировал фотографическое изображение метеорного следа на экран (при помощи эпидиаскопа) в сильно увеличенном масштабе и выполнял рисунки границ туманной полосы и деталей ее строения. Затем определялись их положения путем линейной интерполяции отрезков прямых линий, соединяющих изображения звезд. Очевидно, что не представляет труда найти по ним часовые углы (для чего надо вычислить местное звездное время снимка).

Зная t_i и δ_i, можно нарисовать изображение следа, со всеми замеченными подробностями, на гномонической сетке.

Проделав те же самые операции со вторым снимком, мы получим на одной гномонической сетке два изображения одного и того же следа. Нанеся на эту карту положение точки 0\ и проводя через нее прямые линии, мы сумеем определить координаты соответственных точек.

Каждая пара синхронных снимков даст возможность определить высоты и положения тех точек земной поверхности, в которых выделенные детали следа находятся в зените, т. е. нарисовать фигуру следа в трех измерениях.

При наличии нескольких пар синхронных снимков можно будет изучить динамику развития следа и, в частности, установить, с какими скоростями и в каких направлениях двигались отдельные образования, на которые распался след.

На рисунке 122 приведены результаты такой обработки метеорного следа, снимки которого были получены из двух пунктов X. Гульмедовым и его сотрудниками. Стрелками показаны направления движений.

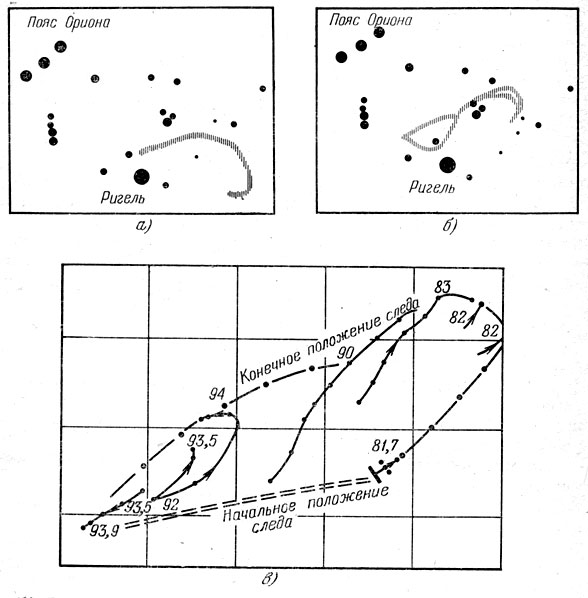
Рис. 122. Движение метеорного следа, сфотографированного из двух пунктов 17/18 ноября 1966 г.: - вид следа в 1ч. 56 м. 51 с. всемирного времени (МВ); б) - вид следа в 2 ч. 00 м. 21 с. МВ (след изменил положение и яркость его ослабела); в) - начальное и конечное положение следа над поверхностью Земли; показаны перемещения отдельных деталей на разной высоте, указанной числами (в км)

Наблюдатель, не имеющий возможности организовать корреспондирующие наблюдения из двух пунктов, может проводить фотографирование из одного пункта. Эти снимки также дадут ценную информацию. Некоторую информацию дадут также прямые визуальные наблюдения. Правда, они требуют от наблюдателя большой тренировки. Необходимо уметь быстро отождествлять вид звездного неба с картой.

Сложность наблюдений состоит в том, что наблюдатель, обнаружив в бинокль (или телескоп) устойчивый метеорный след, сначала проводит наблюдения за его движением, отмечая те или иные положения и моменты времени (что лучше делать секретарю по командам наблюдателя), а затем отождествляет область неба со звездной картой.

Пусть из таких наблюдений мы установили совокупность таких данных: T_i - момент, α_i - прямое восхождение и δi - склонение. Эти наблюдения могут быть обработаны при условии, что мы будем считать высоту следа неизменной и пренебрегать возможными вертикальными движениями.

При обработке мы прежде всего переводим экваториальные координаты в горизонтальные, т. е. получаем азимуты и зенитные расстояния каждой из точек. При этом придется для каждого момента среднего времени вычислить соответствующее ему звездное время.

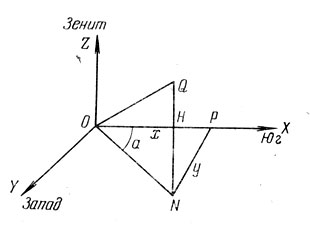
Рис. 123. Координатные оси для вычисления горизонтального дрейфа метеорного следа

Затем выберем пространственную прямоугольную систему координат OXYZ, направив ось ОХ на юг, ось О У на запад и ось OZ в зенит (рис. 123). Из точки Q метеорного следа опускаем перпендикуляр QN на плоскость OXY. Образуется треугольник OQN, в котором, по нашему предположению, катет QN известен и равен Я = 83 км. Тогда отрезок ON = Н tg z. Угол PON равен азимуту а точки Q, и из треугольника OPN находим

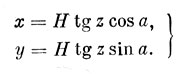
Выполнив эти вычисления для начальной точки, x₁ и y₁ получим х_n и y_n - Проделав то же самое для последней точки, найдем жпи уп. Разделив на промежуток времени t_n - t₁, выраженный в секундах, получим проекции скорости дрейфа v на оси координат:

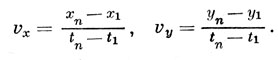
Очевидно, что υ_x - проекция на южное направление, a υ_y - на западное. Величина полной скорости имеет вид

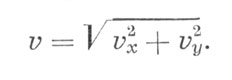
Для определения направления скорости используем формулу

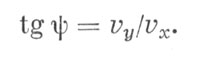
Этот уголг составлен направлением скорости v с направлением на юг и отсчитывается от последнего по часовой стрелке.

Из совокупности таких наблюдений можно построить «розу ветров» в метеорной зоне (рис. 124).

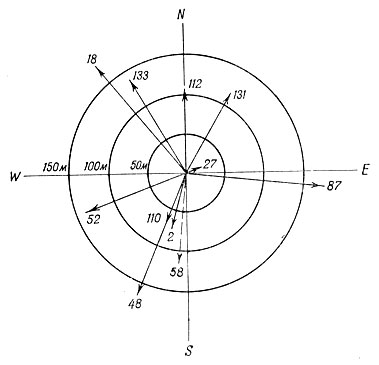
Рис. 124. 'Роза ветров', составленная по наблюдениям метеорных следов в 1948 г. в г. Туле