§ 60. Определение высот метеоров

Одна из основных задач, решаемых корреспондирующими наблюдениями,- определение истинной траектории метеора в атмосфере, и начинается ее решение с определения высот метеора.

Для этого надо прежде всего отыскать на двух видимых траекториях метеоров так называемые соответственные точки.

Рассмотрим рис. 120. На пем буквой М обозначена точка на истинной траектории метеора. Ее мы видим из пункта O₁ в направлении О₁М', а из пункта O₂- в направлении О₂M'. Точки М' и М" называются соответственными, и их координаты нужно найти.

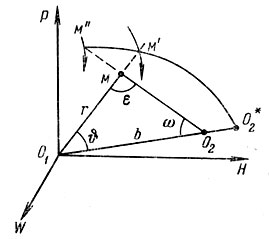
Рис. 120. К отысканию соответственных точек на двух траекториях одного метеора, наблюдавшегося из двух пунктов

Находятся они из того условия, что точки М', М" и O*₁ должны лежать на дуге большого круга, так как треугольник O₁MO₂ - плоский. Угол е в нем определяет параллактическое смещение.

Выбираем на траектории, наблюденной из пункта О₁ точку М' с координатами α', δ' и пишем уравнение большого круга, проходящего через нее (5.8):

Xcosδ'cosα' + Ycosδ'sinα' = - sinδ'. (5.44)

Этот круг должен пройти через точку О*₂ и поэтому ее координаты α*, δ* должны уравнению (5.44) удовлетворять; получается второе уравнение для определения X и Y:

Xcosδ*cosα* + Ycosδ*sinα* = - sin δ*. (5.45)

Решая их совместно, мы получаем значения Х0 и Y0 и после подстановки в уравнение (5.8) находим

X_оcosδcosα + Y_оcosδsinα = - sin δ. (5.46)

Это уравнение отличается от (5.44) тем, что в нем известны Х_о и Y_о, а текущие координаты α и δ - переменные.

Точка М" должна лежать на этом круге и на большом круге, описывающем видимую из пункта О₂ траекторию метеора, и, следовательно, ее координаты должны также удовлетворять уравнению

X₂cosδcosα + Ycosδsinα = - sin δ. (5.47)

в котором Х₂ и Y₂ - величины, характеризующие этот большой круг.

Решая совместно эти два уравнения, получим координаты точки М" (α", δ"). Опуская эти выкладки, приводим окончательные формулы:

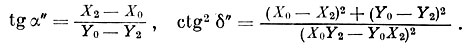
(5.48)

Теперь определим угол параллактического смещения ε. Он находится из формулы (5.1), переписанной для нашего случая в виде

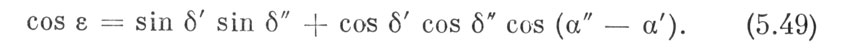
Далее надо определить угол υ между направлениями O₁M и О₁О₂. Этот угол согласно (5.1) определяется из формулы

Обозначив длину базиса O₁O₂ через b, а расстояние O₁М через r, получим из плоского треугольника

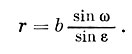
По этой формуле вычисляется расстояние r.

Этого еще недостаточно для вычисления высоты точки М. Для ее получения мы должны соединить точку М с центром С Земли, определить ее расстояние от него и вычесть значение радиуса Земли той точки A, в которой прямая МС пересекает поверхность Земли. Обозначив МС = R и СА = ρ, найдем высоту H = R - ρ.

Таким образом, нам надо определить географические координаты точки А. Для этой цели мы прежде всего найдем прямоугольные координаты точки М по формулам (5.40):

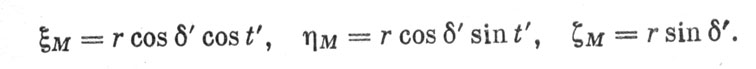
Затем перенесем начало координат в центр Земли и получим геоцентрические координаты точки М

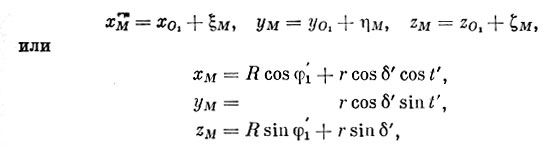
где R = ρ₁ + h₁.

По этим координатам надо вычислить расстояние R_м от центра Земли, геоцентрическую широту точки М (которая равна геоцентрической широте точки А) и ее долготу. Чтобы это сделать, спроектируем точку М на плоскость экватора XCY. Тогда будут получены равенства

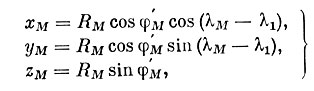
из которых следует, что

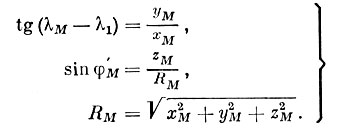
Получив значение φ_м, определяем по формуле (5.29) значение р и находим Н_м.

Эти точные формулы очень громоздки и могут быть заменены приближенными, которые получаются так. Напишем исходные формулы

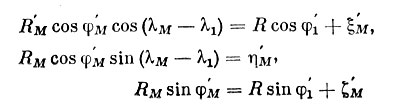
и похожим в них

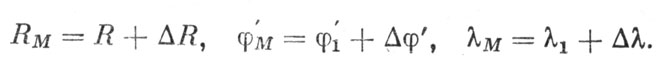
Разделив на R и обозначив

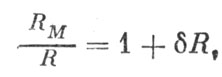
придадим формулам следующий вид:

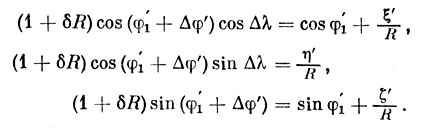
Раскрывая скобки и заменяя ряд значений их приближенными величинами cosΔφ' = 1, cosΔλ = 1, sinΔφ' = Δφ', sinΔλ = Δλ, получаем:

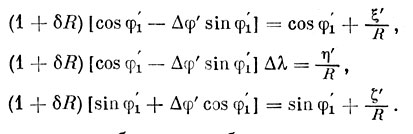
Еще раз раскрывая скобки и пренебрегая произведениями малых величин, получим

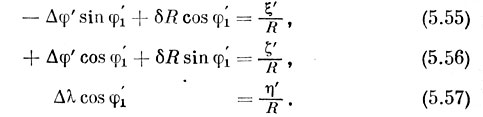
Отсюда получаются нужные нам формулы:

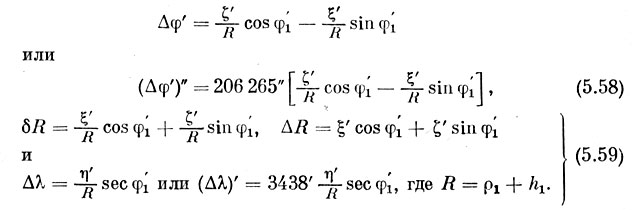
По этим формулам вычисляются приближенные, по достаточно точные значения Δφ' и Δλ, выраженные в угловых минутах, и разность расстояний ДЛ от центра земли.

Обработка визуальных наблюдений в принципе не отличается от обработки наблюдений фотографических, только в этом случае данные о траекториях метеора гораздо менее точны и при выполнении вычислений не надо использовать столько же значащих цифр. Для отыскания соответственных точек можно рекомендовать графический прием решения задачи. При этом следует использовать координатную сетку в гномонической проекции.

Со звездной карты, на которой изображены пути метеоров, снимаем координаты начала и конца видимого пути метеора, α_i и δ_i. Затем, зная момент наблюдения, вычисляем часовые углы t_i.

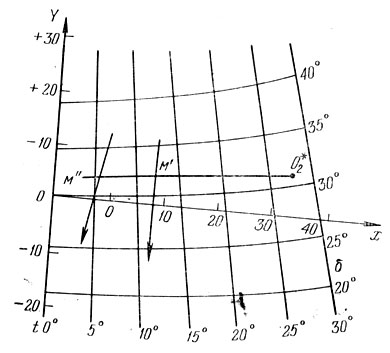
Рис. 121. К отысканию координат соответственных точек с помощью гномонической сетки

Для этого надо вычислить местное звездное время s_i и по формуле t_i = s_i - α_i найти t_i. На гномоническую сетку по координатам t_iи δ_i наносим видимые траектории одного и того же метеора (рис. 121) и положение точки O₂* по ее координатам t_o2*, δо2* - Подготовка окончена.

Выбирая на ближайшей к точке O₂ видимой траектории метеора точку М', -проводим прямую линию М'О₂*. На пересечении этой прямой со второй видимой траекторией метеора лежит точка М", соответственная точке М'. Отсчитываем ее координаты t" и δ". Дальнейшие вычисления идут так, как было описано выше, но с меньшей точностью, для чего можно использовать четырехзначные таблицы тригонометрических функций.