§ 88. Способы наблюдений переменных звезд

Наиболее интересны комплексные фотометрические и спектральные наблюдения переменных звезд. К сожалению, они требуют сложного и дорогого оборудования, которое любителю астрономии недоступно. Вместе с тем для решения важных проблем бывает вполне достаточно визуальных наблюдений и глазомерных оценок блеска переменных звезд при наблюдениях в телескоп или при оценках почернений звездных изображений на фотографических снимках. Методы оценок одни и те же как при наблюдениях в телескоп, так и на фотографических снимках. При этом надо только помнить, что оценка блеска имеет точность около 0,07 звездной величины, и выбирать для наблюдений объекты, у которых амплитуда превосходит 0,3 звездной величины.

Если же любитель астрономии располагает возможностями организации фотоэлектрических, более точных наблюдений, то ему рекомендуется прочитать главу VIII книги «Переменные звезды и способы их исследования» («Педагогика», Москва, 1970) В. П. Цесевича, написанную Ю. А. Медведевым. Она рассчитана на любителя астрономии, знакомого с радиотехникой, умеющего читать и составлять радиотехнические схемы и узлы.

Приступая к наблюдению избранной переменной звезды, надо прежде всего найти ее на небе (или на снимке). В этом помогут звездные атласы, описанные в § 8. Особенно удобным для этой цели является атлас А. А. Михайлова, на картах которого помечены переменные звезды. К нему добавлена небольшая книжка, в которой приведен каталог всех нанесенных на карты переменных звезд с указанием координат, амплитуд и типов переменности. Помогает при наблюдениях также и карта окрестностей переменной звезды, на которой изображены и более слабые звезды. Такие карты помещены в упомянутой книге В. П. Цесевича.

Отождествив переменную звезду, надо привыкнуть быстро ее находить; это даст экономию времени при наблюдениях.

Следующая задача - подобрать удобные звезды сравнения. Надо, чтобы они были расположены как можно ближе к переменной звезде и были сравнимы с ней по блеску и желательно по цвету. На зарисованной карточке окрестностей необходимо обозначить звезды сравнения какими-либо буквами и стремиться в дальнейшем эти обозначения не путать.

После этого надо приступить к оценкам блеска. Для этого служат три метода, которыми должен последовательно овладеть наблюдатель.

Первый, самый старый, способ был предложен Аргеландером. Он состоит в следующем. Если, вглядываясь поочередно в звезду сравнения а и переменную υ, мы видим, что они не отличаются по блеску, то мы пишем а υ. Если же после длительного сравнения мы видим, что а чуть-чуть светлее, чем υ, то мы пишем aiv и говорим, что а на одну степень светлее υ.

Если мы обнаруживаем различие в блеске двух звезд уверенно, но только после внимательного их сравнения, то мы пишем a2v. Более значительное различие блеска оценивается как аЗу, а4г;. Большее количество степеней употреблять не рекомендуется. Если разность в блеске а и г> стала большей, то надо прекратить сравнение с а и выбрать другую звезду. Вообще же одно наблюдение состоит из нескольких сравнений с тремя-четырьмя звездами, из которых некоторые должны быть ярче переменной, а некоторые слабее ее. Например,

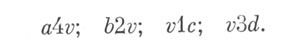
На первый взгляд метод Аргеландера кажется ненадежным, и некоторые наблюдатели предпочитают пользоваться методом Пиккеринга, который заключается в следующем. Подбирают две звезды сравнения, из которых одна чуть ярче переменной звезды, а другая слабее. Вглядываясь в них поочередно, оценивают интервалы в десятых долях разности блеска звезд сравнения, например, a1υ9b, а8υb, a8υ2b или в общем виде apυ (10 - р) b. Обозначение более яркой звезды всегда записывается первым. Такой, чисто интерполяционный способ кажется более надежным.

Существует еще третий метод, который синтезирует оба описанных. Этот метод предложен Нейландом и Блажко. В каждой оценке блеска должны быть использованы две звезды сравнения- более яркая и более слабая, чем переменная звеада. Затем, сравнивая интервалы, устанавливается число степеней в меньшем интервале. Так, например, оценка a4υ2b означает, что интервал в блеске υ,b оценен в две степени, а интервал а и υ оказался в два раза большим, т. е. равным четырем степеням. В таком случае допускаются оценки в 5, 6 и 7 степеней.

Для обработки наблюдений, проведенных по способу Пиккеринга, надо знать звездные величины звезд сравнения, а они далеко не всегда известны. Кроме того, надо иметь в виду, что приведенные в каталогах звездные величины могут не совпадать с теми, которые приходится использовать при вычислениях, так как «цветоощущение» глаза наблюдателя (или фотографической эмульсии) является «индивидуальным». Методы Аргеландера и Нейланда - Блажко дают возможность построения шкалы блеска звезд сравнения, которую в ряде случаев можно затем перевести в шкалу звездных величии. Таким образом, метод Нейланда - Блажко является наиболее совершенным и широко используется. С течением времени, по мере накопления опыта, у наблюдателя вырабатывается устойчивая величина степени, и кажущаяся неуверенность устраняется.

Итак, пусть накоплено достаточное число оценок блеска. Теперь можно приступить к их обработке. Прежде всего надо вывести шкалу блеска звезд сравнения.

Для этого образуют все значения разностей. Пусть, например, была сделана оценка a4υ2b. Тогда разность блеска звезд сравнения b - а = 6. Составив все разности b - а, вычисляют из них среднее значение b - а = а.

То же самое выполняют и для интервала блеска с - Ь. Пусть его среднее значение равно с - b = β. Далее, пусть d - с =γ. Обозначив блеск звезды а символом (а), блеск звезды b - символом (b) и т. д., получаем систему уравнений, в которой неизвестных на единицу больше числа уравнений:

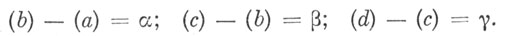
Теперь принимаем блеск самой яркой звезды равным нулю и, решая уравнения, получаем очевидные равенства:

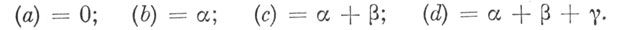
Шкала блеска готова. Можно приступить к вычислению блеска переменной звезды. Покажем, как обработать оценку cpvqd. Согласно полученной шкале разность (d) - (с) = γ. В нашей оценке она равна р + q. Следовательно, в данном отдельном наблюдении цена степени отличалась от средней. Вычисляем ее значение η, разделив γ на

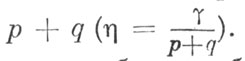
Теперь, умножив полученное значение т па р и прибавив к блеску более яркой звезды (с), мы получим блеск переменной звезды: При таких вычислениях большую помощь оказывает логарифмическая линейка.

Так как каждое наблюдение состоит из оценки блеска и момента наблюдений, мы получаем после обработки совокупность пар чисел: момент наблюдения Т и величина блеска s. Момент наблюдений лучше всего выражать в юлианских днях и их десятичных долях (см. § 18).

В ряде случаев степенная шкала может быть преобразована в шкалу звездных величин, если для нескольких звезд сравнения известны по каталогу (или какому-либо другому источнику) звездные величины. Для более полного решения этой задачи надо знать также и показатели цвета.

Если бы цветовые системы каталога и наблюдателя были одинаковыми, то можно было бы считать, что звездные величины и степенная шкала связаны простыми уравнениями вида

m = m₀ + sp

где m₀ - нуль-пункт степенной шкалы, а р - величина степени.

Назовем такое уравнение двучленным. Приняв такую зависимость, мы можем написать для каждой звезды, у которой известна звездная величина, уравнение (8.3) и получить систему:

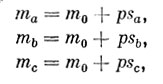
и т. д., которая решается по способу наименьших квадратов относительно неизвестных m⁰ и р (см. Дополнение I). Найдя их численные значения, мы подставляем их в формулу (8.3), в которой теперь остаются неопределенными величины s и m. Подставляя в полученную формулу найденные при обработке значения 5, мы вычислим блеск переменной, выраженный в звездных величинах «приведенной» шкалы. Так можно вычислить и «индивидуальные» звездные величины звезд сравнения m', исходя из данных о степенной шкале их блеска.

В том случае, когда известны еще и показатели цвета, надо воспользоваться трехчленным уравнением

m = m_o + ps + cC

в которое введены показатели цвета С с «коэффициентом цветности» системы с. Решив систему уравнений по способу наименьших квадратов, мы определим m₀, р и с. Тогда формула (8.4) примет численный вид, но вычислять звездные величины переменной звезды по ней нельзя, так как мы не знаем показателей цвета переменной звезды, которые изменяются. Поэтому в данном случае, получив m_o и _р, надо подставить их значения в двучленную формулу (8.3) и вычислять звездные величины переменной звезды. Это, конечно, операция не вполпе строгая.