§ 89. Построение кривой изменения блеска

Получив пары чисел (Т,s) или (Т, m), исследователь может приступить к построению кривой изменения блеска переменной звезды. Теперь все зависит от свойств наблюдавшейся звезды.

Если переменная звезда изменяет свой блеск медленно, то строится общая кривая блеска. Выбрав соответствующий масштаб чертежа, откладывают на горизонтальной оси графика, слева направо, время, а на вертикальной оси - блеск (так, чтобы он возрастал вверх). Изобразив на рисунке все точки, проводят по ним плавную кривую, конечно, сглаживая ее до некоторой степени за счет случайных ошибок наблюдений. Из такой кривой можно определить элементы экстремумов - максимумов или минимумов, т. о. моменты и величину максимального или минимального блеска.

При этих определениях используется способ хорд Погсоыа. Выбрав на восходящей и нисходящей ветвях сглаженной кривой точки равного блеска, соединяют их хордой, которую делят пополам (рис. 194). Соединяя такие «срединные» точки плавной линией, продолжают ее до пересечения с кривой блеска. Здесь находится экстремум (максимум или минимум), и остается только отсчитать по осям графика момент и соответствующий блеск.

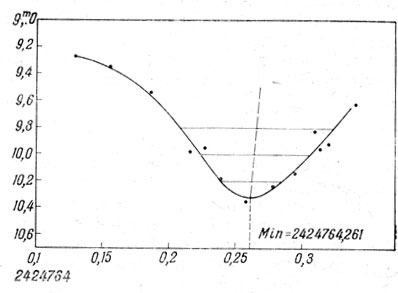
Рис. 194. Определение момента минимума способом хорд

Если наблюдалась долгопериодическая звезда типа Миры Кита, то~моменты М максимумов блеска (которые чаще определяются из наблюдений) должны связаться между собой той же формулой (8.1):

М = М_о + Р х Е,

где М₀ - начальный момент максимума, а Р - по-прежнему период.

Для придания этой формуле численного вида, надо заимствовать из каталога переменных звезд величины М₀ и _Р для данной звезды. Вычислив по формуле ближайший момент максимума, соответствующий некоторому целому Е, назовем его М_выч. Разность М_набл - М_выч) меньшая половины периода Р, называется поправкой эфемериды.

Если наблюдается полуправильная или неправильная неременная звезда, которая не имеет периода, то вычисляют разности моментов максимумов. Такая разность называется величиной индивидуального цикла и часто обозначается буквой С. Из многолетних наблюдений определяют большое число значений цикла и образуют гистограмму, откладывая на горизонтальной оси продолжительности циклов, а на вертикальной - численности. Из гистограммы определяются среднее значение цикла и полуширина гистограммы. При отыскании продолжительности циклов используют не только моменты максимумов, но и моменты минимумов блеска.

У некоторых неправильных звезд, таких, как вспыхивающие и вспышечные, изменения блеска иногда происходят настолько быстро, что надо строить индивидуальные кривые блеска для каждой ночи. В таком случае выбирается столь подробный масштаб времени, что построение общей кривой блеска становится невозможным. Моменты вспышек или ослаблений определяются тем же способом Погсона, но в данном случае моменты определяются точнее.

При изучении короткопериодических звезд, в тех случаях, когда за одну ночь произведено много наблюдений, производят такое же построение индивидуальных кривых блеска и определяют моменты максимума или минимума блеска. При этом надо обязательно учесть орбитальное движение Земли.

При перемещении Земли по орбите ее расстояние от звезды периодически меняется с периодом, равным году. Поэтому все наблюденные моменты необходимо приводить к центру Солнца, т. е. исключать из них влияние изменений расстояния. Это выполняется по формуле

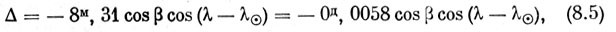
где 8,31 минуты - промежуток времени, в течение которого луч света пробегает средний радиус земной орбиты, β - эклипти-кальная широта звезды, λ - ее эклиптикальная долгота, а λ_о -эклиптика льная долгота Солнца. Зная экваториальные координаты звезды, можно по формулам (2.12) вычислить ее эклиптикальные координаты λ и β, а λ₀ надо взять из Астрономического Ежегодника. Вычислив поправки Δ, прибавляют их к моментам наблюдений, после чего последние получают название гелиоцентрических и обозначаются Т_hel. Эти поправки шдо придавать только в том случае, если период звезды короче 5 суток.

Иметь набор индивидуальных моментов экстремумов очень полезно, так как это дает возможность исследовать быстрые изменения периода, такие, как эффект Блажко. Поэтому, если медленно изменяющуюся переменную звезду достаточно наблюдать один-два раза в ночь, то короткопериодические звезды типа RR Лиры надо наблюдать через каждые 5 - 10 минут, учащая наблюдения во время восходящей ветви кривой. Точно так же надо наблюдать и затменные звезды. Надо стремиться определять индивидуальные моменты экстремумов. Однако последнее оказывается не всегда возможным. Так, например, у затменной звезды U Цефея редко удается пронаблюдать полный минимум блеска за одну ночь. Тогда приходится строить среднюю кривую блеска, объединяя в ней наблюдения, выполненные в разные ночи.

Для построения средней кривой блеска надо воспользоваться исходной формулой (8.1),

M_E = M_o + P x E

где под М можно понимать момент максимума для пульсирующих звезд и минимума - для затменпых. За начальный момент М₀ может быть также избран любой другой, например, момент перехода блеска через определенное значение на восходящей ветви кривой. Будем называть этот момент «нулевым».

По этой формуле вычисляется эфемерида, для чего полезен арифмометр или любая другая счетная машина. Затем, имея перед собой список вычисленных эфемеридных нулевых моментов, исследователь выбирает тот из них, который является ближайшим предшествующим моменту наблюдений Т. Разность моментов Т и M_E называется возрастом наблюдения φ:

φ = T - M_E

а вся операция называется «приведением к одному периоду». Совершенно очевидно, что все возрасты наблюдений заключаются в пределах от нуля до величины периода Р.

Полезно также ввести понятие о приведенном возрасте φ, для получения которого надо величину φ разделить на Р(φ = φ : Р). Теперь можно все наблюдения нанести на общий график, отложив на его гоизонтальной оси φ, а на вертикальной - блеск. Этот график позволяет судить о точности наблюдений, о возможных изменениях кривой блеска и о правильности примененной формулы (8.1). Возможны случаи, когда формула (8.1), приведенная в Каталоге, является неправильной, и тогда надо искать правильную формулу на основании своих наблюдений.

Убедившись, что точки располагаются на таком графике более или менее узкой полосой, можно приступить к вычислению средней кривой блеска. Для этого расписывают все наблюдения в порядке возрастания величин φ, распределяют их по группам и внутри каждой группы вычисляют средние значения возраста и блеска. Графическое изображение средней кривой должно для надежности охватывать по времени больше периода, как показано на рис. 195. Проведя сглаженную кривую, определяют способом хорд момент экстремума. Для этого надо отсчитать возраст фм точки максимума (или минимума) и превратить его в возраст φм = φм x Р. Это дает поправку эфемериды.

После этого из всего ряда наблюдений надо найти средний момент, называемый эпохой наблюдений. Выбрав из вычисленной ранее эфемериды момент, наиболее близкий к эпохе наблюдений, прибавляем к нему найденную поправку эфемериды и находим средний наблюденный момент экстремума.

Теперь надо остановиться еще на одном важном вопросе. При осреднении длительных рядов наблюдений применение формулы (8.1) может оказаться неправомочным. Допустим, что эта формула была найдена не очень точно. Тогда при вычислении возрастов мы будем допускать ошибки, которые будут накапливаться с увеличе- , нием интервала, охваченного наблюдениями. Поэтому рекомендуется не сразу строить общую среднюю кривую блеска, а разбивать наблюдения по «сезонам». Особенно это касается фотографических наблюдений, которые обычно растягивают на длительное время, получая всего один-два снимка в ночь.

Производят построение средней сезонной кривой блеска и из нее определяют средний сезонный момент максимума. За короткий срок ошибка формулы (8.1) не успевает накопиться. Тогда из полного ряда наблюдений, разбитого па сезонные группы, будет получено несколько моментов экстремума, и надо убедиться в том, что поправки эфемериды не изменяются систематически. Для этого выписывают номера моментов Е и величины М_набл - М_выч = 0 - С. Если они изменяются, систематически нарастая или уменьшаясь, то формула (8.1) требует улучшения. Оно выполняется так. Обозначим поправку нулевого момента через ДМ0, а поправку значения периода через ДР. Тогда должна быть справедлива формула.

Из нее легко получить систему условных уравнений. Для этого мы вводим в нее номера Е и величины О - С. Величины поправок мы считаем неизвестными и решаем систему уравнений по способу наименьших квадратов. Получив поправки, прибавляем их к исходным значениям М0 и Р формулы (8.1), после чего снова вычисляем новую эфемериду и сравниваем ее с наблюдениями. Если теперь нет систематического хода О - С с E, то улучшенная формула может быть использована для вычисления возрастов и для построения единой средней кривой блеска.

Из средней кривой блеска определяются асимметрия ε = Мах - Min/P для пульсирующих звезд, а также продолжительность затмения D и продолжительность его полной фазы d для затменных звезд. Также полезно отметить глубину и возраст φ вторичного минимума блеска затменной звезды, если такой минимум заметен.

На практике часто встречаются случаи изменения периода. Тогда стремятся разбить весь интервал времени, охваченный наблюдениями, на части и определить для каждой из частей подходящие значения М₀ и Р. Как это сделать, подробно рассказано в книге «Переменные звезды и способы их исследования» В. П. Цесевича.