§ 91. Первичное определение периода

До сих пор мы предполагали, что элементы периодической переменной звезды уже достаточно точно определены, т. е. что в нашем распоряжении имеется формула (8.1). Как же ее получить в том случае, если звезда совсем не исследована, но мы убеждены, что она является периодической?

Легче всего отыскать период звезды типа Миры Кита. Допустим, что из наблюдений определены надежные моменты ее максимумов M₁, М₂, М₃, ..., M_k. Образуем разности последовательных моментов М₂ - M₁, M₃ - М₂, .., M_k - M_k-1 и ищем такое наибольшее Р, которое уложилось бы с достаточной точностью в каждой из этих разностей, будучи умноженным на целое число. Затем, выбрав первый момент за начальный, составляем предварительную формулу (8.1), вычисляем эфемериду, находим О - С и номера Е и улучшаем эфемериду способом наименьших квадратов, как было описано в § 89.

Приведем пример. Из наблюдений найдены моменты максимумов М₁ = 2427843, М₂= 2428061, М₃ = 2428941, М₄ = 2429361. Разности М₂ - М₁ = 218, М_з - M₂ = 880, М₄ - M_з = 420. Из их сравнения очевидно, что число 216 подойдет для пробной формулы (8.1), которая получает такой вид:

MaxJD = 2427843 + 216 x E.

Эту формулу надо улучшить по способу наименьших квадратов. В следующей таблице приведены остатки О - С от значений, вычисленных по этой формуле:

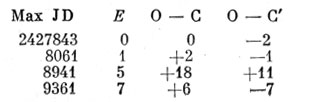
Исходя из Е и значений О - С, напишем уравнения:

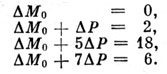
Решение по способу наименьших квадратов дает значения поправок ΔM_о = + 1,^Д6 ≈ +2^Д, ΔР = +1,^д5, так что формула становится такой:

MaxJD = 2427845 + 217?5 x E.

Отклонения от этой формулы приведены в последнем столбце О - С'.

Значительно сложнее определяется период короткопериоди-ческой звезды, особенно затмешюй. Очень трудно найти значение периода, если обрабатываются изолированные фотографические наблюдения, так как из них моменты экстремумов определяются неточно. Дело в том, что моменты экстремумов могут быть удалены друг от друга на большие промежутки времени и трудно устано-новить, сколько между ними протекало периодов, т. е. найти правильное значение Е.

Подробные визуальные наблюдения в этом отношении гораздо лучше фотографических, так как из них легче получить точные моменты экстремумов. Для этого надо строить индивидуальные кривые блеска из наблюдений, выполненных на протяжении одной ночи. Допустим, что у нас имеются в распоряжении три надежно определенных момента минимума блеска затменной звезды T₁, Т₂ и Т₃. Обозначим неизвестное значение периода через Р. Тогда, очевидно, должны быть справедливы два уравнения:

T₂ - T₁ = PN₁ и T₃ - T₂ = PN₂

где N₁ и N₂ - неизвестные целые числа.

Разделим эти уравнения, исключив неизвестное Р, Получим

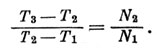
Обозначим отношение (T₃ - T₂) : (T₂ - T₁) = Q.

Тогда будет справедливо уравнение N₂ = QN₁, содержащее два неизвестных N₁ и N₂; оно неразрешимо. Однако, так как оба неизвестных должны быть целыми числами, можно задать одному из них совокупность целых чисел и отобрать те значения второго, которые также будут целыми (или мало отличающимися от целого). Отбирая такие пары, мы выведем из трех моментов минимумов все возможные значения периода Р, которые затем надо проверять по всей совокупности наблюдений. Если есть хотя бы четвертый момент минимума, то он позволит осуществить проверку. Если же его нет, то надо с каждым значением периода строить свою среднюю кривую блеска и искать согласия или противоречия по всем наблюдениям.