«Великолепная теорема» Гаусса

Давайте вспомним или познакомимся с тем, как обычно геометры характеризуют кривизну искривленной поверхности в окрестностях избранной точки М. Прежде всего они строят плоскость, касательную к поверхности в исследуемой точке, и восстанавливают перпендикуляр. Затем проводят через перпендикуляр множество секущих плоскостей. Каждая из них пересекает поверхность по какой-то кривой, которую вблизи точки М можно считать частью окружности большего или меньшего радиуса. И вот оказывается, что окружности самого большого и самого маленького радиусов лежат всегда во взаимно перпендикулярных плоскостях сечения. Геометры берут величины, обратные этим радиусам (их называют главными радиусами кривизны), и перемножают:

1/R_max • 1/R_min = K.

Получают, полную, или гауссову, кривизну.

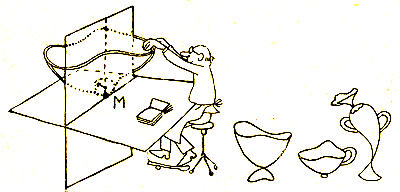
«Великолепная теорема» Гаусса

Конечно с точки зрения двухмерных жителей искривленной поверхности касательная плоскость, перпендикуляр к ней, секущие плоскости и все, что выходит за пределы двухмерного мира,— все это недоступно пониманию двухмерного разума, все это для него мираж, нереальность и фантастика. Как же быть?.. И вот Гаусс доказал, что полная кривизна может быть без всяких дополнительных построений выражена через результаты измерений на самой поверхности. Понимаете, независимо от внешнего, окружающего пространства! Это открытие получило название «великолепной теоремы».

Красиво, правда? Любили предки оформлять свои достижения. Любили и умели, нужно отдать им должное.

«Великолепная теорема» Гаусса

Величие гауссовой теоремы заключается в том, что полная кривизна абсолютно характеризует поверхность в исследуемой точке. Она доступна жителям двухмерного мира и определяет ту геометрию, которую следует им применять. Плоскуны и плоскатики могут вообще не иметь понятия, что такое «кривизна» собственного мира. Но, получив путем измерений абстрактную величину гауссовой кривизны, равную нулю, они должны пользоваться самым простым типом геометрии — эвклидовой. Если же число К окажется на всей поверхности одинаковым и больше нуля, ряд постулатов Эвклида теряет смысл и нужно применять законы другой — сферической геометрии.

Вообще говоря, «внутренняя» и «внешняя» геометрий могут сильно отличаться друг от друга. Возьмем, например, три геометрические фигуры: плоскость, цилиндр и конус. Внешне выглядят они совсем по-разному. А внутренняя их суть?..

Давайте раздвоимся. Пусть одна наша половинка расплющится и перейдет жить на плоскость, ну хотя бы на лист этой книги. Вторая же часть пусть продолжает сидеть или лежать, держа уцелевшей рукой книгу перед уцелевшим глазом. А теперь аккуратно свернем лист в цилиндр или в конус-кулек и зададим своей расплющенной половинке несколько вопросов.

— Эй, двухмерный, как там у тебя с геометрией?

— Все так же. Как была эвклидовой, такой и осталась...

— Подожди, разве ты не чувствуешь изменений?

— Нет. Гауссова кривизна равна нулю по-прежнему.

И ведь он прав, наш двухмерный двойник. У плоского листа бумаги оба радиуса кривизны, R₁ и R₂, имеют бесконечно большое значение. Следовательно, произведение их обратных величин даст нуль. Но нуль можно получить, имея и один радиус бесконечным. Значит, и цилиндр и конус будут обладать внутренней геометрией, неотличимой от эвклидовой на плоскости.

Другое дело, если бы нам пришла в голову фантазия превратить, плоский лист бумаги в сферу. Впрочем, вряд ли это кому-либо удастся, не сминая листа в складки или не разрывая его поверхности. Сфера — поверхность совсем другого характера, чем плоскость, и потому ее внутренняя геометрия не такая, как у плоскости. И кривизна ее имеет положительное значение, а не равна нулю.

Фактически Гаусс заложил основы совсем новой геометрии, опирающейся на опыт, на измерения, а не на постулаты. Правда, его исследования касались лишь поверхностей двух измерений. Но это была тропа, которая должна была вывести математиков на широкую дорогу обобщений.