Метеориты кольца Сатурна

Метеоритами, обнаруженными в Солнечной системе, являются не только те, которые падают на нашу собственную планету, но и те, которые постоянно кружатся около далекого Сатурна.

Замечательное тонкое кольцо, окружающее Сатурн, является, можно сказать, украшением не только его самого, но и украшением всей Солнечной системы. Для человека, в первый раз приникающего глазом к телескопу, после Луны - это, пожалуй, наиболее любопытное зрелище. Этим зрелищем и мы, и Сатурн обязаны метеоритам.

Однако понадобилось больше двух веков, чтобы разгадать природу этого исключительного и единственного образования в нашей Солнечной системе.

Галилей, направлявший свой телескоп то на одно, то на другое светило и почти всякий раз открывавший что-либо неожиданное и не укладывавшееся в рамки птолемеевых и средневековых представлений о Вселенной, был очень озадачен «поведением» Сатурна. В свой несовершенный телескоп, не дававший четких изображений и увеличивавший всего лишь в 30 раз, Галилей увидел по бокам Сатурна какие-то придатки. Что это за придатки, разглядеть ему никак не удавалось. Между тем Галилей видел в действительности «ушки» кольца, т. е. части кольца сбоку от планеты и темные промежутки, отделяющие кольцо от шара планеты. Эти промежутки внушили Галилею мысль, что у Сатурна по бокам находятся две меньшие планеты, нечто вроде спутников. Ведь открыл же он четырех спутников, сопровождающих Юпитер наподобие свиты. Нечто подобное может быть, вероятно, и у Сатурна, - думал Галилей, а рассмотреть кольцо, существование которого никто бы и придумать не мог, - было невозможно.

Рис. 60. Сатурн и его кольца

Кто из ученых, стоявших на пороге замечательного открытия, не трепетал, снедаемый двойственным чувством: ревнивой гордости и опасения грубой ошибки! Сообщить о поразительной новости, как говорится, «и хочется и колется».

Во времена Галилея ученые находили из этого положения такой выход. Обнародовалась шифрованная краткая запись об открытии, расшифровать которую, кроме автора, никто не мог. Проходило время, автор успевал проверить окончательно свое открытие и тогда расшифровывал свое предварительное загадочное сообщение, сохранив, таким образом, за собой первенство (приоритет). К этому способу прибег и Галилей, опубликовав такую шифрованную запись, называемую анаграммой:

Smaismrmielmepoetaleumibuvnenugttaviras

Эти латинские буквы, переставленные в должном порядке, образовывали фразу на латинском языке (на котором тогда по преимуществу писали ученые всех стран), извещающую об открытии Галилея.

Нетерпеливый должен быть терпелив! Кто хочет поторопиться узнать об открытии, - переставляй эти буквы в разном порядке до тех пор, пока не получится осмысленная фраза! А кто поручится, что из этих же букв нельзя составить совершенно другую фразу?

В математике теория сочетаний позволяет сосчитать, сколько перестановок (с повторениями) можно сделать из этих 39 букв. Их число равно

39! / 5! 3! 2! 2! 5! 2! 4! 2! 3! 3! 4!,

что составляет 35-значное число! (Везде восклицательный знак после цифры означает произведение всех целых чисел от 1 до этого числа, например 39! означает: 1Х2Х3Х4Х... Х38Х39.)

Едва ли вы решитесь на попытку расшифровать эту запись! Но Кеплер, знаменитый современник Галилея, один из основоположников современной астрономии, решился. Прославленное терпение Кеплера, без которого он не мог бы открыть свои знаменитые законы движения планет, было беспримерно. И Кеплер расшифровал анаграмму Галилея (опустив 2 буквы) так:

Salve, umbistineum geminatum Martia proles.

В переводе на русский язык это означало:

«Привет вам, близнецы, Марса порождение»

и отражало предположение Кеплера, что у Марса должны быть два спутника, которые и открыл Галилей.

Кеплер думал, что у Марса, как планеты, находящейся между Землей с одним спутником и Юпитером с четырьмя спутниками, тогда только что открытыми, должно быть именно два спутника. Как известно, у Марса действительно обнаружили два спутника, но лишь 2 1/2 столетиями позднее, а у Юпитера их известно теперь уже не 4, а 13.

Увы, труд Кеплера оказался напрасным, ибо анаграмма Галилея, расшифрованная им позднее, после исключения 2 букв (а их он включил в тайнопись, чтобы труднее было догадаться) означала:

Altissimum planetam tergeminum observavi,

т. е.

«Высочайшую планету тройною наблюдал»,

так как Сатурн, как наиболее удаленная от Солнца планета среди тогда известных, назывался «высочайшей» планетой. Аллегорически Галилей писал еще, что Сатурна (названного так в честь дряхлого бога Времени и Судьбы) поддерживают по бокам двое служителей...

Увы, скоро служители покинули своего старца, так как через несколько уиет Галилей перестал видеть эти придатки и усомнился в своем открытии. Дело же заключалось в том, что в определенные периоды Сатурн на своем пути около Солнца поворачивается так, что его тонкое кольцо обращается к Земле своим ребром. Тогда оно не видно даже в самые сильные телескопы, а за несколько дней до «исчезновения» оно видно лишь, как тончайшая светлая игла, «пронзающая» шар Сатурна. В телескопы средней силы, а тем более в такой, какой был у Галилея, кольцо совершенно перестает быть видимо; кольцо, как говорят, исчезает.

Это выражение не раз вело к недоразумениям и, например, в 1921 г. ряд провинциальных газет напечатал сенсационное сообщение своих ретивых, но мало осведомленных корреспондентов о том, что «Кольцо Сатурна пропало!», т. е. разрушилось, а некоторые из них уже совсем от себя добавляли: «и осколки его летят к Земле, грозя столкновением».

Кольца Сатурна, «исчезая» каждые 15 лет, на самом деле нам не доставляют этим никакой неприятности, а наоборот, оказывают как бы любезность, позволяя обнаружить их крайнюю тонкость. Правильную модель кольца Сатурна мы получим, если вырежем из тончайшей бумаги кольцо около 30 cm диаметром.

В 1966 г. за девять месяцев Земля трижды пересекала плоскость Сатурнова кольца и оно исчезало, а дважды оно было видно своей теневой стороной, оставаясь узким. Следующий раз такое событие произойдет в 1980 г. Иногда кольцо поворачивается или, как говорят, раскрывается, так что оно все прекрасно видно, но никогда все же мы его не видим «плашмя», никогда его края благодаря проекции не принимают форму круга, каковыми они являются на самом деле.

Распознать кольцо Сатурна и объяснить изменения его вида удалось лишь лет через пятьдесят после Галилея голландскому ученому Гюйгенсу. Но и он, как Галилей, начал с опубликования анаграммы

Ааааааа, ссссс, d, eeeee, g, h, iiiiiii, 1111, mm, nnnnnnnnn, oooo, pp, q, rr, s, ttttt, uuuuu

и лишь через три года, окончательно убедившись в правильности своих первоначальных заключений, сообщил смысл этой загадочной группы букв:

Annulo cingitur, tenui, piano, nusquam cohaerente, ad eclipticam inclinato,

или

«Кольцом окружен тонким, плоским, нигде не прикасающимся, к эклиптике наклоненным».

Позднее в кольце была обнаружена темная щель, концентричная с его краями, делящая кольцо на две части - внутреннюю и внешнюю, или на кольца «А» и «В». Она получила название щели Кассини, по фамилии ученого, впервые ее заметившего. Потом были обнаружены еще щель Энке, более узкая, и «креповое кольцо», самое внутреннее и едва светящееся. Поэтому часто говорят не о кольце, а о кольцах Сатурна.

Со временем стало выясняться, что кольцо Сатурна не сплошное, и не только в том смысле, что это не одно сплошное кольцо.

Не раз замечали, что через кольца просвечивают звезды и при этом почти не ослабляются в свете. Значит, в них много промежутков и весьма больших, через которые звезда светит как лампочка сквозь решетчатое окно. Кроме того, однажды видели, как один из спутников Сатурна погрузился в то место, где должна была располагаться тень колец. В тени внешнего яркого кольца спутник перестал быть видим, но в тени внутреннего кольца его яркость лишь слегка ослабилась. Значит, внутреннее кольцо довольно прозрачно, а во внешнем кольце просветов между частицами очень мало.

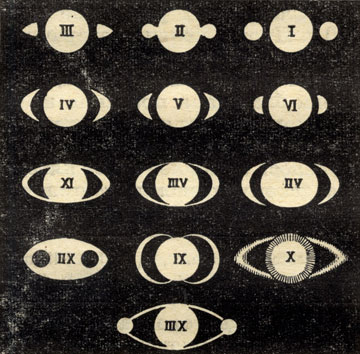
Рис. 61. Старинные зарисовки Сатурна

Теоретические исследования устойчивости кольца, подверженного притяжению Сатурна и притяжению открытых впоследствии спутников этой планеты, показали, что сплошное твердое или жидкое кольцо было бы разрушено этим тяготением. Оно не могло бы существовать, а раз так, то, очевидно, существующее кольцо состоит из отдельных небольших, но чрезвычайно многочисленных кусочков, - кусочков такого размера, какого бывают метеориты. К такого рода заключениям пришло несколько ученых, изучавших этот трудный математический вопрос.

Окончательно и бесспорно метеоритное строение кольца Сатурна доказали академик А. А. Белопольский и Килер (США). Замечательный ученый, один из основоположников астрофизики, Белопольский совершенно правильно рассудил, что спектральный анализ может тут сказать решающее слово. Если кольцо сплошное и вращается как твердое тело с одинаковой угловой скоростью, то линейная скорость вращения частиц кольца должна расти пропорционально их расстоянию от центра Сатурна. Если же кольцо состоит из отдельных метеоритов, то каждый из них должен двигаться около Сатурна независимо от других по своей собственной орбите, как маленький спутник планеты. В этом случае скорость их движения должна определяться законами Кеплера, и внутренние части кольца должны вращаться быстрее наружных.

Рис. 62. Изменение вида колец Сатурна

Смещение спектральных линий (по принципу Доплера) позволяет определить скорость источника света относительно наблюдателя. Один край сатурнова кольца приближается к нам при вращении, другой с такой же скоростью удаляется. Белопольский получил спектр от разных частей кольца и убедился в том, что действительно скорость внутренних частиц в кольце (20 км/сек) больше скорости наружных частиц (16 км/сек). Мало того, оказалось, что скорости частиц в зависимости от их расстояния от центра Сатурна меняются в точности, как это должно быть при движении по законам Кеплера: квадраты периодов их обращений пропорциональны кубам их расстояний от центра планеты.

В 1934 г. академик Г. А. Шайн в Симеизской обсерватории в Крыму вновь исследовал спектр Сатурна, но уже с другой целью. Его интересовал размер частиц сатурнова кольца, который непосредственно определить не удается. Ведь будь эти метеориты в несколько километров поперечником, их дисков на таком огромном расстоянии все равно не было бы видно. Они представляются просто светящимися точками, которые благодаря густоте своего расположения и многочисленности сливаются для нас в яркое и сплошное на вид кольцо.

Сравнение спектра кольца Сатурна со спектром Солнца показало, что между ними нет заметных различий, а это означает, что частички кольца должны быть во много раз больше длины световой волны, т. е. значительно больше тысячной доли миллиметра. Если бы они являлись пылинками, у которых размеры сравнимы с длиной световой волны, то из состава падающего на них солнечного света они рассеивали бы сильнее всего голубые лучи. В результате кольца Сатурна отражали бы голубые лучи лучше, чем остальные, их цвет был бы голубее цвета Солнца, и голубая часть спектра колец была бы ярче, чем в спектре Солнца. Так же как частицы такой мельчайшей пыли, ведут себя и молекулы воздуха. Это их свойство и придает небу голубой цвет, делает голубую часть спектра неба более яркой, чем в спектре Солнца, свет которого молекулы воздуха рассеивают и делают дневное небо светлым. По распределению энергии в спектре света, отраженного кольцом Сатурна, оно очень сходно с обыкновенным льдом, но не с замерзшей углекислотой. По-видимому, частички кольца покрыты слоем льда или даже состоят из него.

К сожалению, из упомянутых данных нельзя определить наибольшую возможную величину частиц сатурнова кольца, - нет ли среди них таких, которые подобны обычным метеоритам, падающим на Землю, или даже таких, которые по своей величине сравнимы с мелкими астероидами. Изучение изменения яркости колец в зависимости от угла, под которым мы на них смотрим, приводит к выводу, что среди составляющих их частиц большинство отбрасывает довольно длинные тени и, следовательно, имеет размеры скорее порядка размеров метеоритов, чем размеров метеоров.

Доктор физико-математических наук М. С. Бобров, будучи моим учеником, еще до Великой Отечественной войны заинтересовался тайной строения кольца Сатурна и впоследствии, сопоставив все данные оптических и других наблюдений, заключил, что в среднем частицы кольца имеют размер около метра. В позднейшей работе он получил значительно меньшие размеры - от 0,35 до 35 мм. Обнаруженная затем медленность прогревания частиц кольца Солнцем после выхода их из тени говорит в пользу первого вывода: о более крупном размере частиц. В пользу частиц порядка метра снова говорят результаты радиолокации Сатурна, осуществленной впервые в 1973 г. От самой планеты отраженный радиосигнал не был получен, а от кольца сигналы отразились с большей силой, чем ожидалось. Из этого был сделан вывод, что кольцо состоит из метровых, а может быть, и больших глыб угловатой формы.

Внутреннее, креповое кольцо Сатурна оказывается по данным академика Г. А. Шайна более голубоватым, т. е. оно отчасти должно состоять и из мельчайших пылинок, по размерам сравнимых с длиной световой волны.

Полная ширина кольца Сатурна так велика, что по нему, как по дорожке, свободно мог бы катиться земной шар, диаметр которого (12 740 км) в пять раз меньше ширины кольца. Из трех его главных частей - средняя наиболее яркая и плотная (кольцо «В») шириной 26 000 км. Щель Кассини, отделяющая от него самое внешнее кольцо «А», имеет в ширину 5000 км, а ширина кольца «А» - 16 000 км. Полупрозрачное, креповое кольцо «С» светится слабо и позволяет видеть сквозь него поверхность планеты; его ширина 18 000 км. Представьте себе теперь, что при такой ширине толщина колец лежит в пределах 1 1/2 - 3 км!

Заключение об общей массе кольца можно вывести, исходя из теории его устойчивости. Масса колец не больше 1/4 массы Луны и, вероятно, гораздо меньше, как это было найдено из наблюдений над возмущениями, производимыми в движении спутников Сатурна притяжением кольца. Кольца и спутники взаимно возмущают друг друга.

Насколько больше солнечного света отражает эта небольшая масса, чем та же масса, собранная в один шар! Если бы четверть лунной массы мы превратили в метеориты и разместили их в кольце кругом Земли, то получили бы освещение в тысячи раз более сильное, чем то, которое получаем теперь от своего спутника.

Как интересно было бы перенестись на Сатурн и любоваться оттуда его кольцами!

Увы, тут нас ожидало бы разочарование, так как от полюса до широты 64° на Сатурне кольца не видны вовсе - их загораживает выпуклость шара самой планеты и лишь в экваториальной области планеты между широтами +35° и -35° видна вся ширина колец. Однако здесь они видны всего лишь под углом 12° и меньше, поднимаясь над горизонтом наподобие радуги, а с экватора планеты они видны совсем с ребра - в виде яркой, но очень узкой полосы, проходящей через зенит и делящей все небо пополам. Если еще учесть, что одна сторона колец освещена, а другая темная, то мы придем к заключению, что на любом из полушарий Сатурна кольца можно видеть только в течение полугода. Речь идет, конечно, о сатурновом полугодии, равном нашим 15 годам. Большей частью в эпоху видимости колец на данном полушарии Сатурна они видны днем, от чего красота зрелища проигрывает, а ночью часть кольца покрыта тенью самой планеты. Наконец, если вспомнить, что Сатурн вечно окружен облаками, сплошным покровом окутывающими его атмосферу, то мы придем к заключению, что практически, перенесясь на Сатурн, мы бы с него колец вообще никогда не видели. Итак, если хотите лучше всего рассмотреть метеоритные кольца Сатурна, то не переселяйтесь на Сатурн! Лучше всего их можно было бы рассматривать с какого-либо из спутников этой планеты, но опять-таки под небольшим углом, почти с ребра.

Рис. 63. Воображаемый вид колец Сатурна из верхних слоев его атмосферы

Быть может, некогда один из таких спутников Сатурна, ближайший к нему и вознамерившийся было подойти еще ближе, был наказан за свою дерзость тем, что был обращен в метеоритное кольцо.

Французский математик Рош еще в 1850 г. доказал, что жидкий спутник какой-либо планеты, находясь к ней ближе некоторого предельного расстояния, должен быть разорван на части приливными силами. Для спутника, имеющего плотность, одинаковую с плотностью планеты, этот «предел Роша» составляет 2,44 радиуса планеты. Ближайший из спутников Сатурна, Мимас, отстоит от его центра на 3,11 радиуса планеты, а внешний край кольца - на 2,30 радиуса Сатурна. Итак, кольцо Сатурна целиком находится внутри предела Роша, внутри зоны, запретной для спутников, желающих сохранить свою целость. Это подтверждает справедливость теории Роша и возможность образования кольца за счет разрушения одного из спутников, который либо начал было образовываться в этой зоне при рождении Солнечной системы, да так и не смог образоваться, либо же он попал в нее извне благодаря возмущениям. Заметим, однако, что для твердого сплошного спутника предел Роша будет гораздо меньше, чем для жидкого тела.

В 1966 г. было открыто самое широкое внешнее кольцо Сатурна, названное кольцом D. Его размер вдвое больше, чем система колец, известная ранее. Но это кольцо крайне разрежено. Открытый в 1966 г. спутник Янус и более далекий спутник Энцелад двигаются внутри кольца D, как в сопротивляющейся среде, Мимас же лишь пересекает кольцо D, потому что его орбита наклонена к плоскости кольца. Эти новые данные согласуются с последним нашим замечанием, касающимся предела Роша.

Щели в кольцах образовались вследствие возмущения движения метеоритных частиц притяжением спутников Сатурна. Там, где период обращения частиц соизмерим с периодом одного из внутренних спутников, возмущения особенно велики и делают орбиты частиц неустойчивыми. В тех местах, где периоды обращения частиц составляют 1/2, 1/3 или 1/4 от периода обращения близких спутников, эти частицы задерживаются недолго, и эти области почти не заняты их орбитами, а значит, и самими частицами, - там образуются пустоты, щели. Такие же прогалины наблюдаются и в орбитах астероидов, в тех местах, где их периоды обращения были бы соизмеримы с периодом обращения Юпитера.

Щель Кассини в кольцах соответствует периодам обращения, равным 1/2 периода обращения Мимаса, 1/3 и 1/4 периодов обращения двух следующих спутников Сатурна. Аналогичные соотношения встречаются и для других щелей, наблюдаемых в кольцах.