
§ 5. Первые загадки Урана
Уран оказался самой сложной и интересной планетой с точки зрения небесной механики XIX века. История Урана с первых же дней его открытия и до середины XIX века - это цепь научных неприятностей, недоразумений и замечательных достижений. Началось прежде всего с того, что при первых наблюдениях Урана астрономы, так сказать, обознались. Вильям Гершель, а затем и остальные астрономы приняли его сначала за комету. Первое официальное сообщение Гершеля 26 апреля 1781 года о его открытии в Лондонском Королевском Обществе было озаглавлено «Сообщение о комете». Многие известные астрономы, например, Лаплас, Жозеф Лаланд (1732-1807) пытались по наблюдениям нового небесного тела (тогда название Уран ему еще не было дано) вычислить для него параболическую орбиту, характерную именно для комет. Считалось, что это небесное тело находится недалеко за пределами земной орбиты.
Все открывавшиеся до тех пор кометы (кроме кометы Галлся) двигались по параболам (рис. 11) или близким к ним гиперболам. Обычно кометы обнаруживались тогда, когда они подходили сравнительно близко к Солнцу и к Земле. После этого кометы все более приближались к Солнцу, причем довольно быстро, и как бы почти на глазах становились все более яркими. Затем кометы так же быстро удалялись от Солнца и Земли, теряли свою яркость и растворялись в глубинах небес.
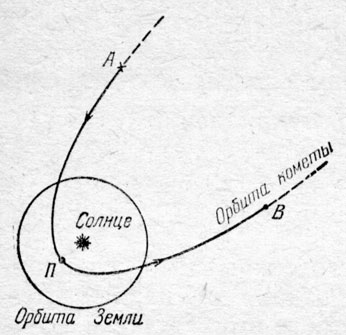
Рис. 11. Изображение параболической орбиты кометы. А и В - точки, разделяющие часть орбиты, на которой комета видна невооруженным глазом
В случае же ноной «кометы» оказалось, что ее теоретическое движение по любой такой орбите должно быть гораздо более быстрым, чем фактически наблюдаемое ее движение. Расчетное и видимое движения совпадали не более, чем на несколько дней, а затем новая «комета» быстро «отставала» от расчетных данных. Новая «комета» оказалась странной. Она почти не меняла яркость и ее быстрого приближения к Солнцу, обычного для всех комет, не обнаруживалось. Первая загадка!
В мае 1781 года французский астроном Жан Сарон (1730-1794) по данным наблюдений вычислил, что эта «комета» находится гораздо дальше от Солнца, чем предполагалось, и что перигелий ее орбиты находится на расстоянии 12 а. е. от Солнца, т. е. ее орбита целиком находится вне орбиты Сатурна.
Но разве такие кометы бывают?
Как уже упоминалось выше, петербургский академик Лексель определил летом 1781 года по двум наблюдениям, выполненным В. Гершелем 17 марта 1781 года и Невилем Маскелайном 11 мая того же года, что новое небесное тело движется вокруг Солнца приближенно по кругу с радиусом 18.93 а. е. и с периодом около 84 лет. После этого все, наконец, осознали, что новое небесное тело - это планета.
Первая загадка расхождений между теорией и наблюдениями разрешилась. Вскоре были получены астрономами другие варианты круговой орбиты, несколько отличающиеся друг от друга радиусом, расположением в пространстве и начальным положением планеты. Теперь расчетное движение по одной из таких орбит более или менее совпадало с наблюдениями.
Однако совпадение было именно лишь приблизительным. Напомним, что к этому времени методы астрономических наблюдений сильно усовершенствовались. Еще в конце XVII столетия английский астроном Джон Флемстид (1646-1719) - основатель и первый директор Гринвичской обсерватории, первым стал регулярно применять при определении положений небесных светил часы и телескопы со специальными приспособлениями (перекрестные нити в поле зрения, перемещающиеся с помощью микрометрического винта). Таким путем он сумел добиться огромного выигрыша в точности по сравнению с прежними наблюдениями невооруженным глазом. Точность положений звезд и планет у Флемстпда составила 10" (секунд дуги). Лучшие же наблюдения Тихо Браге имели точность 2' и такой же точностью обладал лучший из старых каталогов звезд - каталог польского астронома Яна Гевелия (1611-1687), опубликованный в 1687 году. Позднее лучший наблюдатель своего времени, известный английский астроном Джеймс Брадлей (1692-1762) довел точность наблюдений до 4"-6". К концу XVIII - началу XIX столетий средняя точность наблюдений звезд и планет повысилась уже до 3".
Отклонения Урана по долготе от равномерного движения по кругу проявлялись весьма отчетливо даже в течение одного месяца, достигая более 20". Было очевидно, что надо искать не круговую, а эллиптическую орбиту, так как именно по такой орбите движение является неравномерным. В 1783 году по наблюдениям за два предыдущие года Лаплас и другой французский астроном - Пьер Мешэн (1744-1804) определили приближенно эллиптическую орбиту Урана. Однако элементы этой орбиты были явно неточными, так как не хватало точных наблюдений. Отрезок видимой траектории, пройденной Ураном между звездами за два года, был слишком мал - лишь около 8°,5. Достаточно точное определение всех элементов орбиты по такому малому ее участку было затруднительным. Даже период обращения Урана мог быть определен лишь с точностью примерно в десять дней (Точность определения периода в процентах равна приближенно точности определения видимого отрезка пути, пройденного Ураном. Если погрешность каждого положения Урана составляет 5', то погрешность длины отрезка в 8° равна 0,035%. Этот процент от периода в 84 года составит 0,029 года или 10,6 суток)).
Известному немецкому астроному Иоганну Боде пришла идея, что Уран мог наблюдаться астрономами раньше, но его принимали тогда за обычную звезду. Перелистывая старые записи наблюдавшихся звезд (в них указывались моменты наблюдений и соответствующие координаты звезд), Боде осенью 1784 года обнаружил в списках немецкого астронома Тобиаса Майера (1723-1762) звезду, наблюдавшуюся 25 сентября 1756 года и не наблюдавшуюся позднее. Расчет с помощью приближенных элементов орбиты показал, что в указанном Майером месте и в указанный момент должна была находиться новая планета Уран. Это было первое обнаруженное «старое»» наблюдение Урана, зарегистрированное тогда, когда Уран принимали за звезду. Вскоре Боде и немецкий астроном Фпкслмплнер (1721-1791) обнаружили аналогичным образом «старое» наблюдение Урана, выполненное еще раньше, а именно 23 декабря 1690 года Флемстидом. Точность наблюдений Флемстида составляла, как мы уже говорили, 10", а Майера - еще выше: 5"-6". Промежуток времени с 1690 по 1784 год охватывал уже больше одного оборота Урана вокруг Солнца и вполне можно было уже надеяться на точное определение элементов эллиптической орбиты. Такие элементы были вычислены в 1784 году Фикслмилнером по двум упомянутым «старым» и двум «новым» (после открытия) наблюдениям Урана (в 1781 и 1783 гг.). Он получил следующие элементы орбиты Урана на 1 января 1784 года:
| большая полуось | а=19,18254 а.е. |
| среднее угловое движени в юлианский год (365,25 суток) | n=4°,28487 |
| эксцентриситет | е=0,0461183 |
| долгота перигелия | 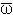 =167°31'33" =167°31'33" |
| средняя долгота | λ=104°40'58" |
| наклон к эклиптике | i=0°46'20" |
| долгота восходящего узла | Ω=72°50'50" |
Элементы эллиптической орбиты планеты изображены на рис. 12. Таких элементов - шесть. Два элемента (большая полуось а и эксцентриситет е) определяют форму и размеры эллипса, угловое расстояние перигелия от узла ω определяет ориентацию эллипса в своей плоскости, долгота восходящего узла Ω и наклон i определяют положение орбитальной плоскости относительно основной координатной плоскости (чаще всего в качестве таковой берется плоскость эклиптики).
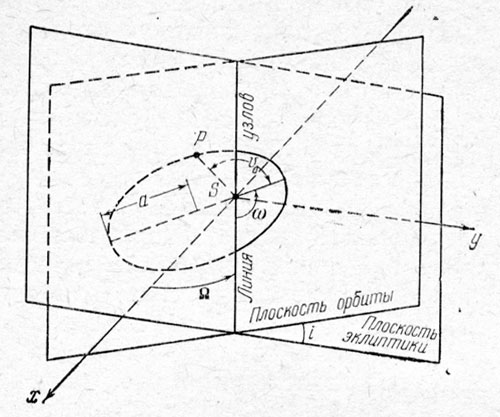
Рис. 12. Элементы эллиптической орбиты планеты Р
Наконец, положение планеты на орбите в некоторый начальный момент t0 определяется углом υ0 (начальным значением истинной аномалии). Вместо угла υ0можно задавать или значение средней аномалии M0 в этот же момент, или эксцентрической аномалии Е0, или средней долготы l0, или истинной долготы υ0. Существуют простые формулы, связывающие Величины υ0, М0, Е0, l0, v0.
Долгота перигелия 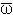 дается формулой
дается формулой
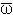 =ω+Ω.
=ω+Ω.
Приведенные выше значения элементов орбиты Урана были достаточно точными. Они отличались сравнительно мало от фактических. Например, позднее на основании наблюдений до 1820 года было найдено а=19,182729 а. е., е=0,0466108, 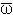 =167°30'24" (на 1 января 1800 года).
=167°30'24" (на 1 января 1800 года).
Несколько иные элементы были вычислены вскоре с помощью этих же «старых» и дополнительных «новых» наблюдений другими астрономами. Расчетные положения Урана, соответствующие этим орбитам, были достаточно близки и к двум «старым» и ко всем «новым» наблюдениям, и, казалось, что Уран, как и другие испытанные временем планеты, больше не будет причинять астрономам особых забот. Казалось, что надо будет лишь несколько уточнять время от (Времени элементы его орбиты по мере накопления наблюдательных данных.
Поясним, что значит уточнять элементы орбиты.
Предположим, что планета движется по некоторой эллиптической орбите, но элементы этой орбиты мы знаем неточно. Тогда возникает задача уточнения пли, как говорят, улучшения орбиты. Дело в том, что если элементы орбиты определены по наблюдениям планеты па одном участке видимого движения, то при дальнейших наблюдениях расчетное и наблюдаемое движения расходятся. Это бывает потому что, во-первых, по малому отрезку видимой траектории элементы орбиты определяются не совсем точно и, во-вторых, движение планеты на самом деле происходит не точно по эллиптической орбите в соотвстстнпп с законами Кеплера. Но каковы бы ни были причины расхождений, ставится все же задача такого исправления элементов (нахождения таких их поправок), чтобы новая исправленная эллиптическая орбита достаточно хорошо отвечала всему фактически наблюдаемому движению планеты. И если фактическое движение не особенно сильно отклоняется от кеплерова движения на интервале времени, охваченном наблюдениями, то такой процесс улучшения (исправления) орбиты приводит к хорошим результатам.
Сама методика улучшения орбиты основана на следующих соображениях.
При изучении гелиоцентрического движения планеты наиболее чувствительной, т. е. наиболее сильно изменяющейся координатой, а потому и наиболее удобной для анализа, является долгота планеты (истинная долгота, отсчитываемая вдоль самой орбиты). Вместе с тем истинная долгота - достаточно удобно измеряемая при наблюдениях координата планеты.
Истинная долгота Урана, - обозначим ее через ν, - определяется (с точностью до 0°, 01) следующей формулой в соответствии с (4):
ν=λ+5°,34 sin φ+0°,16 sin 2φ, (6)
где λ, - средняя долгота Урана, соответствующая равномерному движению по окружности, φ - его средняя аномалия. При этом λ=104°,68+nt, φ=297°, 15+nt, n - среднее угловое движение, а время t отсчитывается от момента, на который задана данная система элементов. Отклонение истинной долготы от средней, т. е. разность ν-λ, обусловлена кеплеровым движением по эллипсу и называется уравнением центра. С точностью до 0°, 0,1 это отклонение представляет собой сумму двух синусоид: основной с амплитудой 5°, 34 и периодом
Т=2π/n=84,014 года
и дополнительной с периодом T/2 и амплитудой 0°,16. Точная формула для ν содержит еще и другие члены, выражающие более мелкие (с амплитудой около 20" и менее) и более быстрые колебания. На графике уравнения центра с масштабом 1° в 1 см была бы практически заметна только основная синусоида.
Если мы несколько изменим элементы орбиты, прибавив к ним малые поправки δε, δn, δ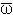 , δe, то выражение для ν также изменится. Поправка к выражению (6) определится приближенно формулой
, δe, то выражение для ν также изменится. Поправка к выражению (6) определится приближенно формулой
δν=δε+tδn+2δe*sinφ-2eδ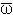 *cosφ. (7)
*cosφ. (7)
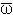 *cosφ. (7)
*cosφ. (7) (δε - поправка к начальному значению средней долготы, обозначаемой через ε)
Это так называемая линеаризованная формула, выражающая зависимость 6v от первых степеней поправок и пригодная, естественно, при малых поправках. Точная формула должна была бы содержать члены с квадратами, кубами поправок и т. д. Вместо (7) используют также более точную линеаризованную формулу
δν=(δε+tδn)(1+2e*cosφ)+(2*sinφ+5/2e*sin2φ)δe-(2*cosφ+5/2e*cos2φ)eδ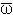
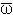
Поправка большой полуоси δа связана с δn формулой
δа=(-2/3)δn.
Обычно среднее движение п определяется достаточно точно. Например, значение л для Урала, определенное Леверье в 1876 году после почти ста лет многочисленных и точных наблюдений, равно 4°, 2846855 и оно сравнительно мало отличается от значения Фикслмиллера. Поэтому разность в долготе δν для двух близких кеплеровых орбит, с элементами ε, n, ... и ε+δε, n+δn, ... соответственно, имеет характер синусоидального колебания с основным периодом 84,014 года и амплитудами порядка 2δe и 2е δω.
При наблюдениях фиксируются в разные моменты расхождения между расчетными и фактическими значениями ν. Обозначим эти расхождения через νн-νв (νн - наблюдаемая долгота, νв - вычисленная долгота)). Тогда мы приходим к следующей математической задаче: найти такие поправки δε, δn, δе, δ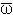 , чтобы δν, вычисленное по формуле (7), было близким ко всем отмеченным значениям расхождений νн-νв на соответствующие моменты. Приравнивая δν и νн-νв на разные моменты времени, мы получим алгебраические уравнения относительно искомых поправок δε, δn, δе и произведения в δω, называемые условными уравнениями. Они будут иметь вид
, чтобы δν, вычисленное по формуле (7), было близким ко всем отмеченным значениям расхождений νн-νв на соответствующие моменты. Приравнивая δν и νн-νв на разные моменты времени, мы получим алгебраические уравнения относительно искомых поправок δε, δn, δе и произведения в δω, называемые условными уравнениями. Они будут иметь вид
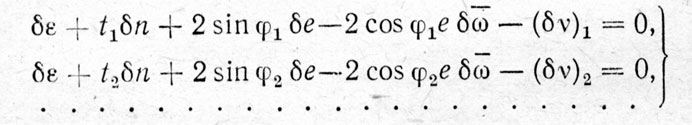
(8)
где t1, t2, ... - известные моменты (точнее, интервалы времени, отсчитываемые от момента, на который заданы элементы орбиты), φ1 φ2, ...- вычисленные на моменты t1, t2,... значения φ, a (δν)1, (δν)2,... равны наблюденным расхождениям.
При этом, поскольку обычно наблюдений много, таких уравнений гораздо больше, чем неизвестных, которых только четыре. Поэтому эти уравнения, как правило, не имеют точного решения. Отсюда название «условные уравнения». При любых значениях неизвестных левые части всех этих уравнений не равны, как правило, одновременно нулю. Сами значения левых частей называют при этом невязками. Чем больше в среднем невязки, тем более плохим считается решение условных уравнений.
Так вот, если фактическое движение планеты близко к кеплерову на данном промежутке времени, который охваче.н условными уравнениями, то найдутся такие поправки δε, δn,..., что все невязки окажутся малыми. Другими словами, все уравнения (8) удовлетворяются одновременно с небольшими погрешностями. Тогда, действительно, новая орбита с элементами ε+δε, n+δn, ... будет отвечать довольно точно наблюденному движению.
Если же фактическое движение сильно отличается от кеплерова, то найти такие хорошие поправки элементов нельзя, т. е. при любых сравнительно небольших δε, δn, ... все или некоторые невязки сравнительно велики (вся методика пригодна, если поправки небольшие). Тогда не существует эллиптической орбиты, которая достаточно точно отвечает наблюдаемому движению.
Метод анализа и решения систем алгебраических уравнений с небольшим числом неизвестных, известный под названием «метод наименьших квадратов», был разработай в 1801 году знаменитым немецким математиком Карлом Фридрихом Гауссом именно для цели улучшения орбит. По этому методу решение таких уравнений находится из условия, чтобы сумма квадратов невязок была наименьшей. Отсюда название «метод наименьших квадратов». Сейчас этот метод применяют очень широко почти всюду, где имеют дело с математической обработкой экспериментальных данных. Это - еще один случай, когда небесная механика дала путевку в жизнь очень важному математическому методу.
Возвращаясь теперь к нашему рассказу об Уране, заметим, что Гаусс разработал и опубликовал свой метод наименьших квадратов позднее того времени, на котором мы остановились (1784 год). Но все же и тогда с задачей улучшения элементов орбит также справлялись, хотя методы были не столь хороши. И, как мы сказали, астрономы надеялись, что в дальнейшем будет достаточно лишь улучшить орбиту Урана, найденную Фикслмилнером.
Однако эти надежды рассеялись уже в 1788 году, т. е. всего через четыре года после определения, казалось бы, точной орбиты. Другими словами, на протяжении лишь четырех лет Уран обнаружил сильные отклонения от кеплерова эллиптического движения
Рассмотрим, например, орбиту Урана с элементами на 1 января 1788 года:
a=19,182524 a.e.,
n=4°,28497,
e=0,045893,
ε=121°58'8"
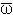 =167°45'2"
=167°45'2"
близкими к элементам Фикслмилнера, оставляя без внимания малое наклонение орбиты к эклиптике (Эти элементы заданы на другой момент времени по сравнению с приведенными выше элементами Фикслмилнера)). Расхождения между наблюденной и вычисленной по этим элементам истинной долготой Урана с точностью до 1" даны в таблице 2.
| № п/п | tк | νн-νв | № п/п | tк | νн-νв |
| 1 | 23/XII 1960 | 0 | 6 | 23/I 1784 | 0 |
| 2 | 25/IX 1756 | 0 | 7 | 16/I 1785 | 10 |
| 3 | 6/I 1782 | 0 | 8 | 13/I 1786 | 23 |
| 4 | 14/X 1782 | 2 | 9 | 14/I 1787 | 71 |
| 5 | 21/XII 1782 | 3 | - | - | - |
Из этой таблицы и из соответствующего графика (рис. 13) для моментов после 1782 года хорошо видно, что данная эллиптическая орбита хорошо отвечает «старым» наблюдениям Урана 1690 и 1756 годов, а также «новым» наблюдениям в 1781-1784 годах. Именно по этим наблюдениям была уточнена орбита и получены элементы, выписанные на стр. 46. Однако также видно, что после 1785 грда Уран быстро уходит вперед по сравнению с расчетным движением.
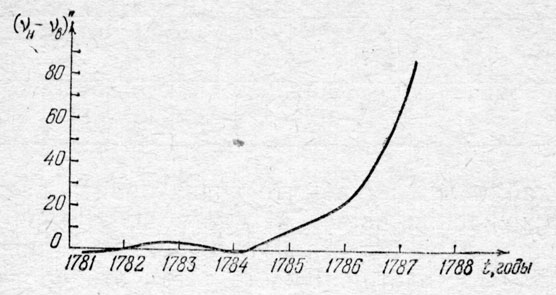
Рис. 13. Расхождение между фактической долготой Урана и вычисленной в случае его эллиптической орбиты
Возникает вопрос, можно ли и далее уточнить элементы орбиты, чтобы хорошо описать и наблюдения после 1785 года?
Ответ на этот вопрос оказывается категорически отрицательным. Фикслмил.нзр очень быстро пришел к такому выводу, пытаясь улучшить элементы по аналогичной таблице расхождений (к сожалению, нам не удалось найти численные результаты Фикслмилнера, поэтому мы провели вычисления заново).
Если использовать таблицу 2, то по формулам (8) получим девять условных уравнений (соответствующих моментам t1, t2, ..., t9) для поправок δε, δn, δе, е δ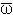 .
.
Эти девять условных уравнении были решены по методу наименьших квадратов на ЭВМ БЭСМ-6. Соответственно округляя, получим
δε=78",
δn=-0",794,
δe=72"=0,00035,
eδ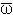 =-56".
=-56".
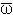 =-56".
=-56".
Внесем эти поправки в элементы и вычислим расхождения между наблюденной и новой расчетной долготой. Тогда вместо таблицы 2 получим таблицу 3.
| tк | t1 | t2 | t3 | t4 | t5 | t6 | t7 | t8 | t9 |
| νн-νв | -1" | 1" | -10" | -5" | -3" | 13" | 14" | 13" | 22" |
Из таблицы 3 видно, что новая орбита дает меньшие расхождения, но все же многие из этих расхождений значительно превышают точность наблюдений в конце XVIII столетия. Вместе с тем эта орбита найдена с помощью метода наименьших квадратов и является в известном смысле наилучшей. Любая другая орбита, близкая к ней, приведет к еще более значительным в целом расхождениям с наблюдениями. Следовательно, невозможно подобрать для Урана кеплерову орбиту так, чтобы она отвечала с нужной точностью (3"-5") всем имеющимся наблюдениям, и «старым» и «новым», до 1788 года.
|
ПОИСК:
|
© 12APR.SU, 2010-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://12apr.su/ 'Библиотека по астрономии и космонавтике'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://12apr.su/ 'Библиотека по астрономии и космонавтике'