
§ 6. Первые победы небесной механики. Проблема Урана как будто решена!
Одним словом, возникла загадка Урана. Правда, тогда казалось, что эта загадка разгадывается в принципе просто. Ведь до той поры никто не анализировал, как влияют на движение Урана другие давно известные планеты, Сатурн, Юпитер, Марс и т. д., а они обязательно должны были оказывать какое-то влияние в силу закона всемирного притяжения Ньютона.
Точно по кеплеровой эллиптической орбите планета двигалась бы лишь тогда, если бы она притягивалась по закону Ньютона только Солнцем, а Солнце и планета были бы материальными точками. Однако по этому же закону притягиваются друг к другу все небесные тела. На каждую планету действует притяжение всех остальных тел Солнечной системы, прежде всего ближайших и наибольших планет. Это притяжение должно вызывать отклонения от кеплерова движения, которое астрономы называют возмущениями. Само фактическое движение планеты называют возмущенным, а идеальное кеплерово движение, которое имело бы место при отсутствии каких-либо возмущений, называют невозмущенным.
До тех пор, пока наблюдения велись невооруженным глазом, и положения планет определялись с точностью до минут дуги, возмущения той или иной планеты оставались довольно долго незаметными. Но, как мы говорили выше, в конце XVII века произошел резкий скачок в технике наблюдений и в их точности. Счет погрешностей в наблюдаемых положениях небесных светил стал вестись уже на секунды дуги. И тогда, конечно, отклонения планет от кеплерова движения оказались, можно сказать, как на ладони. Вместе с тем замечательными работами Ньютона был заложен теоретический фундамент (Удивительное, но часто встречающееся в истории науки совпадение уровня развития экспериментальной и теоретической базы. Действительно, почти одновременно стало возможным и фиксировать при наблюдениях отклонения планет порядка нескольких секунд дуги и теоретически предсказывать и анализировать подобные отклонения. До Флемстнда и Ньютона не было возможным ни первое, ни второе)) для изучения фактического возмущенного движения любых небесных тел, в частности, планет.
Как мы говорили выше, одной из наиболее трудных проблем небесной механики является проблема движения Луны, так как лунная орбита весьма существенно отличается от кеплеровой эллиптической орбиты. Отсюда следует, что возмущения в движении Луны достигают больших значений и их учет только «в первом приближении» не обеспечивает точность, диктуемую наблюдениями. Именно математические трудности проблемы движения Луны стимулировали исследования многих выдающихся ученых XVIII века.
Эйлер в своей второй теории движения Луны, получившей премию Российской Академии наук в 1756 году, разработал новый метод теоретического анализа движений небесных тел. Это - метод оскулирующих элементов, в терминах небесной механики.
Согласно этому методу принимается, что Луна (или планеты) в течение любого небольшого промежутка времени движется по некоторой кеплеровой эллиптической орбите, но сама эта орбита, точнее, ее параметры, т. е. ее элементы, изменяются с течением времени. Говорят, что движение Луны или планеты происходит по оскулирующей орбите или же по орбите, элементы которой испытывают возмущения по сравнению с их постоянными значениями на какой-нибудь момент времени. Можно говорить отдельно о возмущениях большой полуоси, среднего движения, эксцентриситета орбиты и т. д.
Следует различать возмущения элементов орбиты и возмущения в обычном смысле этого слова, под которыми понимают обычно отклонения положений небесного тела от тех, которые отвечают на тот или иной момент кеплерову движению. Чтобы не возникало недоразумений, говорят часто о возмущениях координат или отдельно о возмущениях долготы, широты, радиус-вектора.
Анализ и нахождение возмущений элементов часто бывает более удобным, так как эти возмущения, как правило, малы, в то время как возмущения координат велики. Например, пусть среднее движение п планеты изменяется на 0",01 в год. Это - очень малая величина, которую легко учесть в формулах для вычисления положений планеты. За 100 лет п изменится лишь на 1". Но, например, возмущение долготы планеты за 100 лет достигнет 0",01X1002/2=50", т. е. значительно большей величины.
Кроме того, знание изменений элементов орбиты позволяет часто более наглядно описать качественную картину фактического возмущенного движения.
Этот метод, носящий также название метода вариации параметров, был развит Лагранжем и другими учеными и сейчас он играет большую роль не только в небесной механике, но также в математике и механике (теории дифференциальных уравнений, теории нелинейных колебаний и т. д.).
Опять пример математического метода, родившегося в небесной механике и затем получившего такое широкое применение!
Второй важный для нас момент - тот, что лунные теории служили не только практическим целям вычисления таблиц координат Луны, но и целям проверки справедливости самого закона притяжения Ньютона. Они позволяли выяснить, действительно ли Луна движется в точном соответствии с этим законом, действительно ли наблюдаемые отклонения Луны от кеплерова движения вокруг Земли вызываются ее притяжением другими телами Солнечной системы (причем почти целиком преобладающим является притяжение между Луной, Землей и Солнцем).
Результаты были явно положительными. Разработанные теории отвечали в целом именно тому, что астрономы наблюдали. Правда, мы говорим «в целом» потому, что теории, точно отражающей наблюдения, т. е. не допускающей явно заметных расхождений с данными наблюдений, тогда еще не было. Такие теории оставались в XVIII веке еще недостижимой целью. Луна являлась для теорий слишком сложным объектом. Например, таблицы для Луны, составленные в 1754 году Клеро, давали координаты Лупы, отличающиеся от непосредственно наблюдаемых иногда на 1',5. Таблицы Томаса Манера, изданные первый раз в 1755 году, «ошибались», как правило, на 1'. Техника же наблюдений позволяла фиксировать расхождения в 3"-5".
Первые таблицы движения Луны, ошибки которых оставались сопоставимыми с ошибками наблюдений, были созданы значительно позднее, уже в середине XIX века (Это были таблицы немецкого астронома Пегера Гянзена (1795-1874), директора обсерватории в Готе (Зсеберг). Ошибки таблиц Гапзена по сравнению с положениями Лупы, наблюдавшимися в течение целых ста лет в 1750-1850 голах, не превосходили 1"-2". По такова же была в середине XIX века и точность наблюдений)).
Тем не менее теории движения Лупы в XVIII столетии хорошо отражали основные особенности в наблюдаемых тогда возмущениях.
Конечно, при построении лунных теорлш не все шло гладко. Как всегда бывает при разработке большой, сложной проблемы, возникала иногда ситуация, когда теория, казалось, заходила в тупик, противоречила наблюдаемым фактам. Но затем обнаруживались погрешности в математических исследованиях или в наблюдательном материале, и теория приходила к согласию с наблюдениями.
В первых вариантах теорий Эйлера, Клеро и Даламбера для Луны получалось, что перигей лунной орбиты должен перемещаться (Луна движется по такой оскулирующей эллиптической орбите, которая поворачивается в пространстве) со скоростью около 20° в год. Непосредственно же по наблюдениям Луны получалось, что фактически перигей ее орбиты перемещается почти па 41° в год, т. е. вдвое быстрее. Расхождение между теорией и наблюдениями было таким большим, что некоторые исследователи стали ставить под сомнение закон притяжения Ньютона. Примерно к 1747-1748 гг. начал серьезно ставиться вопрос о внесении в этот закон поправок и замены формулы
F=k2(m1m2/r2)
для силы притяжения другими:
F=k2(m1m2/r2)+α/r3
или F=k2(m1m2/r2)+α/r4
где α - малое число.
По этим предлагаемым формулам сила притяжения не являлась строго обратно пропорциональной квадрату расстояния. Однако в 1749 году Клеро установил, что его теория, а также лунные теории Эйлера и Даламбера являются неполными, их следует уточнить, вычисляя так называемое второе приближение. С учетом таких добавлений расхождения теории c наблюдениями оказывались в основном устраненными. Такой результат явился огромным успехом небесной механики, и сомнения в законе Ньютона превратились в его триумф.
Вторым серьезным препятствием в теории движения Луны явилось наблюдаемое увеличение ее среднего углового движения, которое обнаружил еще в 1693 году английский астроном Эдмунд Галлей, друг и помощник Ньютона. Он анализировал записи о солнечных затмениях в далекой древности по книге «Альмагест» Птолемея и записи о затмениях в средние века. По ним можно было установить видимое положение Солнца между звездами, а вместе с тем и Луны (во время затмения они совпадают) на определенные моменты времени. Затем можно было вычислить на эти далекие моменты среднюю долготу Луны. Сопоставляя значения средней долготы на эти моменты, Галлей заметил, что долгота изменяется с небольшим ускорением, т. е. что среднее угловое движение Луны п постепенно увеличивается. Это был интереснейший наблюдательный факт. После уточнения анализа Галлея было получено, что указанное ускорение составляет около 11" в 100 лет. Вместе с тем из первых теорий движения Луны вытекало, что такого ускорения не должно было бы быть. Опять явное расхождение между теорией и наблюдениями! Опять сомнения в строгости закона Ньютона! Проблема векового ускорения Луны волновала астрономов довольно долго. Лишь к концу XVIII столетия, в 1787 году Лаплас построил, как бы в подарок к столетнему юбилею выхода в свет ньютоновских «Начал», более точную теорию движения Луны и получил, что действительно средняя долгота Луны должна обладать теоретическим ускорением 10",4 в сто лет. Этот результат Лапласа считался в свое время знаменитым. Опять теория пришла к согласию с наблюдениями и опять закон притяжения Ньютона восторжествовал.
В XVIII веке начинаются также работы над теорией планетных движений с учетом взаимных возмущений.
Как мы уже говорили выше, техника наблюдений совершила в конце XVII века качественный скачок и положения небесных светил стали определяться уже с весьма большой точностью (10" и менее), так что явно обнаружились отклонения планет от кеплерова движения. Таким образом, результаты эксперимента (наблюдений) значительноопередили по своему уровню теорию, которая до тех пор описывала движение планет на основании законов Кеплера и его «Рудольфинских таблиц». Понятно, что теория должна была в свою очередь совершить качественный скачок и прийти в соответствие с экспериментом Это - обычный путь развития любой науки: постоянное здоровое «соперничество» теории и эксперимента.
Возможности для решительного нового шага в планетных теориях заключались в строгом применении закона всемирного притяжения. Надо было определить возмущения планет, возникающие благодаря их взаимному притяжению. Принципиально проблема была ясна, но с математической точки зрения она оказалась очень трудной. Она поставила перед учеными такие чисто математические проблемы, из которых далеко не все решены полностью и сейчас.
Естественно, что в начале рассматривались наиболее важные задачи, причем их решения находились с той мерой точности, какую допускали несовершенные еще тогда математические методы. О полных и точных теориях движения планет, Луны, спутников тогда не могло быть и речи.
Мы выше говорили о задаче построения лунной теории, которая, пожалуй, первой стояла на повестке дня. Из планет же первой привлекала к себе сама Земля, поскольку, так сказать, зеркальным отображением ее движения в пространстве являлось видимое перемещение Солнца на небе между звездами. Но по движению Солнца определялась и длина года, и эклиптика, служившая фундаментальной линией па небесной сфере в системах небесных координат. Другими словами, движение Земли тесно увязано с измерением времени (с единицей времени) п с измерением координат всех небесных светил. При наблюдениях невооруженным глазом (с точностью 2'-4') положение эклиптики кажется неизменным в течение 250- 500 лет. Однако если вести наблюдения с точностью до 5", то уже через 10-15 лет обнаружится, ч го эклиптика как бы повернулась вокруг некоторой оси на 5"-1" и ее наклон к экватору уменьшился на эту величину. Точные наблюдения и сопоставление с очень далекими наблюдениями в древности показали, что эклиптика поворачивается примерно на 47" в сто лет. Кроме того, Солнце испытывает кратковременные (короткопериодические) колебания по долготе вдоль эклиптики с амплитудой около 30", которые не объясняются кеплеровым движением по эллипсу (Солнце отклоняется также и от эклиптики, определяемой как некоторый средний путь Солнца. Эти отклонения, достигающие 1",5, оставались в XVIII веке еще незаметными)).
В 1756 году Эйлер получил премию Французской Академии наук за теорию движения Земли с учетом возмущений от ближайших планет в первом приближении. Именно, Эйлер установил факт упомянутого перемещения эклиптики (со скоростью около 0",5 в год). В 1757 году Клеро определил достаточно точно возмущения Земли от Венеры и Луны. Работы по теории движения Земли велись интенсивно и в дальнейшем.
Изучение движений остальных планет, пожалуй, не преследовало в то время сугубо практических целей, как это имело место в случае Луны и Земли. Ставилась скорее чисто научная задача: согласовать теорию, основанную на законе притяжения Ньютона, и непосредственные наблюдения планет. Но при этом, как и в случае Луны, проверялась справедливость и строгость самого закона Ньютона, а этот вопрос привлекал немалое внимание ученых. Кроме того, движения Луны, Земли и других планет связаны друг с другом. Нельзя в принципе строить абсолютно точную теорию Земли, не изучая в деталях движение других планет.
В 1754-1756 годах Днлнмбср опубликовал работу о взаимных возмущениях Юпитера и Сатурна. В 1773 году Лаграпж начал, а в 1784 году Лаплас закончил анализ так называемых больших неравенств в движениях Юпитера п Сатурна (постепенное изменение их средних угловых движений), обнаруженное еще в 1676 году Галлеем п не поддававшееся теоретическому объяснению. Результат оказался таков, что эти возмущения на самом деле являются долгопериодическими с периодом около 900 лет и они возникают именно из-за взаимного притяжения Юпитера и Сатурна. В то же время, в 1773-1784 годах, Лагранж и Лаплас провели замечательные исследования вековых возмущений во всей системе известных тогда планет, решившие, так сказать, в первом приближении, проблему устойчивости Солнечной системы. В частности, был теоретически объяснен наблюдаемый факт медленного вращения эллиптических орбит планет.
Одним словом, все полученные результаты достаточно удовлетворительно согласовывались с наблюдениями планет, и путь для построения точных теорий движения планет представлялся ясным, хотя выдающиеся ученые видели их огромные математические трудности.
Поэтому когда в 1788 году обнаружились заметные отклонения Урана от эллиптического кеплерова движения, то это сильно не удивило астрономов. Ясно, что надо было учесть возмущения Урана прежде всего от самых близких к нему больших планет - Сатурна и Юпитера. Таким образом, объяснение замеченных отклонений представлялось, как говорится, делом техники.
Наиболее серьезные исследования возмущений Урана от Сатурна и Юпитера были выполнены французским астрономом, большим специалистом по истории астрономии, Жаном Батистом Деламбром (1749-1822). Он составил в 1790 году таблицы движения Урана, которые отвечали с нужной точностью (до 5") и двум «старым» наблюдениям Флемстида и Манера, и всем «новым» наблюдениям до 1790 года.
Если принять следующие элементы орбиты Урана (на 1 января 1790 года)
a=19,18339 a.e.,
n=4°,284681,
e=0,046579,
ω=167°13'57"
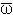 =130°30'59"
=130°30'59"
и пренебречь наклоном его орбиты к эклиптике, то, с одной стороны, вычисленные возмущения истинной долготы Урана от Сатурна и Юпитера (обозначим их через (δν)ю, с), на определенные моменты до 1790 гола оказываются приближенно (с точностью до 1") такими, какие выписаны в таблице 4 (данные взяты из более поздних вычислений Леверье).
| t | (δν) Ю, С | t | (δν) Ю, С | t | (δν) Ю, С |
| 23/XII 1690 | 16" | 23/I 1784 | -23" | 18/I 1789 | 27" |
| 25/IX 1756 | -55" | 13/I 1786 | -36" | 30/X 1789 | 52" |
| 6/I 1782 | 17" | 14/I 1787 | -25" | 24/I 1790 | 58" |
| 21/XII 1782 | -2" | 9/III 1788 | 1" | - | - |
На рис. 14 приведен график этих возмущений с 1782 года по 1790 год. Это - быстро изменяющиеся возмущения: с 1786 года по 1790 год они увеличиваются почти на 100".
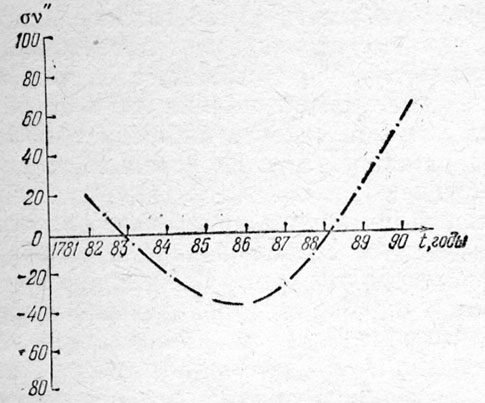
Рис. 14. Возмущения в долготе Урана, обусловленные притяжением Юпитера и Сатурна
Но, с другой стороны, именно такими оказываются расхождения между наблюдавшимися в эти моменты и расчетными значениями долготы в кеплеровом движении. Следовательно, повое расчетное движение Урана, кеплерово плюс влияние Юпитера и Сатурна, достаточно точно отражает наблюдения.
В последующие ближайшие годы расхождения между теорией движения Урана, учитывающей кеплерову орбиту и возмущения Юпитера и Сатурна, и наблюдениями продолжали оставаться небольшими и опять создалось впечатление, что проблема Урана решена. Волнения вокруг этой проблемы утихли, Уран стали гораздо реже наблюдать. Внимание астрономов было привлечено новыми объектами, так называемыми малыми планетами, или астероидами.
|
ПОИСК:
|
© 12APR.SU, 2010-2021
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://12apr.su/ 'Библиотека по астрономии и космонавтике'
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://12apr.su/ 'Библиотека по астрономии и космонавтике'