Приложение 3
Уравнение центра с элементами Леверье для неизвестной планеты имеет вид
ν=240°17'41"+nt+12°,312 sin φ+0°,829 sin2φ+0°,078 sin 3φ, (1)
где n=1°,65603 в юлианский год, φ=-43°,802+nt - средняя аномалия. Радиус-вектор на каждый момент можно вычислить по формуле
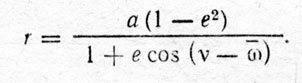
(2)
В этой формуле начальным является момент t=1800,0 и значения v получаются отнесенными к равноденствию этого момента. Формулы (81), (9) (стр. 199) позволяют высчислить значения истинной долготы ν и радиус-вектора r неизвестной планеты (в а. е.) в соответствии с данными Леверье и двумя вариантами данных Адамса. Если дополнительно учесть прецессию и отнести все значения ν к равноденствию на 1850 год, то получим таблицу X.
| t | ν | r в а. е. | ||||
| Леверье | Адамс (1) | Адамс (2) | Леверье | Адамс (1) | Адамс (2) | |
| 1800 | 231°,57 | 237°,46 | 237°,35 | 33,6 | 36,2 | 34,7 |
| 1810 | 251,17 | 252,20 | 256,01 | 32,8 | 34,9 | 33,7 |
| 1820 | 271,47 | 273,14 | 275,57 | 32,4 | 33,4 | 33,0 |
| 1830 | 292,13 | 293,44 | 295,77 | 32,8 | 32,5 | 32,8 |
| 1840 | 312,60 | 314,49 | 316,27 | 32,6 | 32,2 | 32,9 |
| 1850 | 332,42 | 335,60 | 335,89 | 33,3 | 32,4 | 33,4 |
В дальнейшем после открытия Нептуна были получены более точные элементы его орбиты. Если использовать систему элементов на 1 января 1S50 года, приведенную Леверье в т. 13, стр. 110 Трудов Парижской обсерватории
а=30,05568 а. е., n=2°,184704,
е=0,0084962, ω=43°17'30",3, е=335°5'38",9,
а также учесть основные возмущения Нептуна, то получим следующую таблицу его фактических гелиоцентрических истинных долгот ν в орбите и радиусов-векторов r (здесь же приведены значения долготы и радиуса-вектора Урана), отнесенных к равноденствию эпохи 1850 (табл. XI).
| t | Уран | Нептун | ||
| ν | r в а. е. | ν | r в а. е. | |
| 1800 | 174°,79 | 18,3 | 226°,07 | 30,3 |
| 1810 | 221,07 | 18,5 | 247,33 | 30,3 |
| 1820 | 265,23 | 19,2 | 268,87 | 30,2 |
| 1830 | 306,40 | 19,8 | 290,52 | 30,1 |
| 1840 | 345,82 | 20,1 | 312,28 | 30,1 |
| 1850 | 25,15 | 19,9 | 334,20 | 30,0 |
Отсюда получим следующую таблицу расхождений VH - vn между фактической истинной долготой v Нептуна и вычисляемой но Адамсу и Леверье (табл. XII).
| t | νн-νв | ||
| Леверье | Адамс (1) | Адамс (2) | |
| 1800 | -5°,50 | -11°,39 | -11°,28 |
| 1810 | -3,84 | -4,87 | -8,68 |
| 1820 | -2,60 | -4,27 | -6,70 |
| 1830 | -1,61 | -2,92 | 5,25 |
| 1840 | -0,32 | -2,21 | 3,99 |
| 1850 | +1,78 | -1,40 | -1,69 |
|
ПОИСК:
|
При копировании материалов проекта обязательно ставить активную ссылку на страницу источник:
http://12apr.su/ 'Библиотека по астрономии и космонавтике'
