8.5. РАСХОДЫ РАБОЧЕГО ТЕЛА И ЭНЕРГИИ

Для работы двигателей ориентации или ГСС необходима затрата рабочего тела и энергии. В отличие от земных транспортных средств, у которых топливо или подводимая энергия тратится главным образом на преодоление сопротивления среды, а доля, идущая на управление движением, мала, в космосе именно расходы на управление являются нередко определяющими. Если говорить об управлении ориентацией, то обычно основной расход рабочего тела и энергии ДО и ГСС связан с режимами длительного поддержания ориентации.

При использовании ДО возможны два предельных случая: полное отсутствие внешних возмущающих моментов и наличие «большого» возмущающего момента.

Первый случай приводит к так называемым «двусторонним» колебаниям корпуса КА, а второй - к «односторонним» колебаниям; в первом случае попеременно включаются ДО, создающие моменты, противоположные по знаку, включаются попеременно так, чтобы постоянно удерживать угол ориентации в допустимых пределах, а во втором внешний возмущающий момент все время «прижимает» КА к одному из допустимых пределов углов ориентации, а ДО, создающий момент, противоположный внешнему, все время «отталкивает» корпус КА от него в сторону другого допустимого значения углов ориентации.

В первом случае оценка средневременного расхода массы рабочего тела

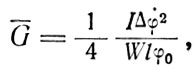
(8.2)

где I - момент инерции корпуса КА;

W - скорость истечения газов из ДО;

l - расстояние от линии действия силы тяги до центра масс КА;

Δφ - приращение угловой скорости КА, сообщаемой ему при однократном включении ДО;

φ₀ - амплитуда колебаний угла ориентации КА.

Из формулы (8.2) видно, что уменьшение 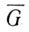возможно за счет увеличения скорости истечения W и плеча силы тяги, а также уменьшения приращения угловой скорости Δφ и увеличения амплитуды колебаний угла ориентации φ₀, или, что то же, получение импульсного включения ДО, дающего минимально возможное Δφ при одном включении и снижение потребной точности ориентации (система управления ориентацией не должна иметь точность выше, чем это необходимо для решения заданной задачи).

Из формулы (8.2) также следует, что нет пределов снижения среднего расхода 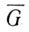за счет уменьшения Δφ или использования ДО очень малой тяги. Однако этому мешает требование совершения (например, при поиске ориентира) достаточно быстрых поворотов, требующих ДО большой тяги. Компромиссное решение сводится к выбору тяги ДО исходя из требований быстроты поворотов КА при непрерывном включении ДО и получении минимального значения Δφ путем использования технически достижимых минимальных по времени импульсных включений ДО.

Во втором случае, когда колебания оказываются односторонними, средневременный массовый расход рабочего тела

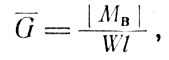
(8.3)

где М_в - внешний возмущающий момент.

Физическая сущность этого равенства очевидна - расход пропорционален внешнему возмущающему моменту М_в и не зависит ни от точности ориентации, ни от величины единичного вращательного импульса Δφ.

В общем случае теоретическое рассмотрение задачи и методика расчетов сильно усложняются. Для предварительной проектной оценки расхода рабочего тела можно предложить простое суммирование обоих видов расхода

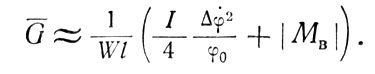
(8.4)

Для ГСС - одностепенных гиростабилизаторов, работающих в импульсных режимах, значения средневременного расхода энергии 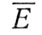аналогичны формулам (8.2) и (8.3), в которых произведение Wl σ- эффективность используемых ДО - следует заменить величиной а - эффективностью использования энергии ГСС, равной

(8.5)

где М_а - развиваемый момент;

N - потребляемая мощность.

При пренебрежимо малом значении внешнего возмущающего момента следует учитывать, что между статором (корпусом КА) и ротором ГСС действует момент сопротивления М_с, который формально будет играть роль внешнего момента М_в в равенстве (8.3).

Что касается двух- и трехстепенных ГСС, характеризующихся постоянством кинетических моментов роторов при большой угловой скорости их вращения, то средневременной расход энергии определяется главным образом затратами на поддержание этой угловой скорости постоянной и не зависит от особенностей процесса ориентации.

Основным внешним моментом, с которым приходится иметь дело при создании ИСЗ, является гравитационный момент, тогда как аэродинамический момент проявляется только на очень низких высотах, а момент от солнечного давления - лишь на межпланетных трассах, где первые два практически исчезают.

Гравитационный момент стремится повернуть КА в положение, при котором его наиболее протяженная главная центральная ось инерции стала бы параллельной местной вертикали. На рис. 8.9 показано протяженное тело S, движущееся по плоской орбите вокруг центра Земли С. Триэдр осей OX₀Y₀Z₀ - триэдр орбитальных осей ориентации, а триэдр OXYZ составлен главными центральными осями инерции тела S. Рассмотрим случай, когда оси Z и Z₀ совпадают и поворот тела относительно местной вертикали определяется углом φ_Z, т. е. имеет место поворот только по тангажу. В этом случае гравитационный момент

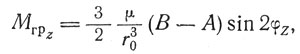
(8.6)

где

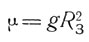
(g - ускорение силы земного тяготения на поверхности Земли, a R_З - радиус Земли);

А и В - главные центральные моменты инерции тела относительно осей ОХ и ОУ;

r₀- расстояние центра масс КА от центра Земли.

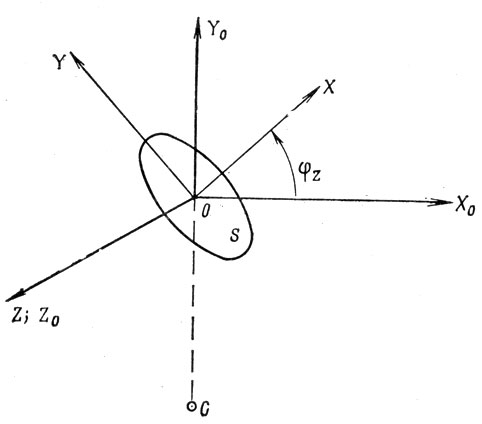
Рис. 8.9. Жестко связанный с телом S триэдр осей OXYZ, повернутый на угол φ_Z относительно триэдра орбитальных осей OX₀Y₀Z₀ (С - центр Земли)

Из формулы (8.6) видно, что при φ_Z = 0 и φ = π/2 гравитационный момент равен нулю, т. е. горизонтальное и вертикальное положение большой оси тела S соответствует положению равновесия. Однако между этими двумя положениями равновесия имеется существенное отличие. Нетрудно убедиться, что устойчивым является вертикальное, а не горизонтальное положение вытянутой оси тела S.

Гравитационный момент может проявиться и при орбитальной ориентации КА, так как жестко связанный с корпусом КА триэдр главных центральных осей инерции OXYZ практически всегда повернут относительно триэдра OX′Y′Z′, определяемого конструкцией КА (конструктивных осей КА). Поскольку датчики системы ориентации и научная аппаратура юстируются в КА относительно его конструктивных осей, в реальном полете ориентируют именно конструктивные оси КА, что делает КА гравитационно неуравновешенным. Величина момента, вызванного несовпадением конструктивных осей и осей инерции, будет возрастать вместе с размерами КА, поскольку гравитационный момент пропорционален моментам инерции, которые, в свою очередь, возрастают пропорционально пятой степени линейных размеров КА. Поэтому для очень больших КА более предпочтителен полет в несколько «повернутом» положении, при котором в гравитационном поле Земли нужное положение заняли бы оси инерции, а не конструктивные оси КА, что может вызвать усложнение логики системы ориентации. Особенно большие повороты эллипсоида инерции относительно конструктивных осей возможны при резком изменении геометрии масс КА (функционировании разного рода массивных поворотных устройств, пристыковке и отстыковке других КА и т. п.).

Другим источником появления больших гравитационных моментов может стать требование удержания корпуса КА неподвижным относительно поступательно движущихся осей ориентации (относительно далеких звезд), например, при астрономических исследованиях, когда угол тангажа может изменяться за один оборот вокруг Земли на величину 2π. Как следует из формулы (8.6), изменение угла тангажа на π/2 является наибольшим возможным интервалом значений φ, внутри которого гравитационный момент М_гр не изменяет своего знака.

Так, при полете вокруг Земли по круговой орбите в начальный момент времени кинетический момент КА равен нулю, угол = 0 и, следовательно, M_гp = 0. Тогда кинетический момент, накопленный КА при полете по 1/4 дуги его круговой орбиты,

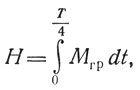
(8.7)

где Т - период обращения ИСЗ вокруг Земли. Интегрируя выражение (8.7), получим

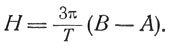
(8.8)

Таким образом, можно избежать включения второго контура исполнительных органов, если система гиростабилизаторов будет в состоянии «поглотить» кинетический момент, имеющий порядок произведения момента инерции ИСЗ на угловую скорость его вращения вокруг Земли. Другим методом радикального уменьшения всех затрат, связанных с возмущающим действием гравитационного момента, является приближение эллипсоида инерции КА к сфере, т. е. приближение разности моментов инерции в формуле (8.6) к нулю.

Гравитационный момент не всегда является помехой и может быть использован для получения нужной ориентации. Если, например, нужна ориентация в орбитальных осях, при которой продольная ось КА была бы все время вертикальной, достаточно привести КА в такое вертикальное положение и придать ему в нужном направлении угловую скорость, равную угловой скорости орбитального движения, после чего гравитационный момент будет удерживать КА в этом положении сколь угодно долго. Такой метод ориентации иногда применялся на орбитальном комплексе «Салют» - «Союз». Возможность полезного использования гравитационного момента привела к возникновению целого направления в космической технике - созданию ИСЗ с пассивными (без затраты рабочего тела и энергии) и полупассивными (без затраты рабочего тела) системами гравитационной стабилизации. Эти системы, позволяя удерживать только постоянную ориентацию ИСЗ в орбитальных осях, имеют ограниченное применение.

Роль гравитационного момента резко возрастает с увеличением массы КА, так как момент инерции КА чрезвычайно быстро растет с увеличением его размеров. При естественных предположениях о зависимости характеристик КА и его агрегатов от линейных размеров КА с ростом последних прямо пропорционально возрастают и относительные запасы рабочего тела. Это приводит к тому, что с увеличением размеров КА использование ДО для управления ориентацией все более и более затруднительно. Поэтому, начиная с некоторой величины КА, особенно при длительных полетах, необходимо применение ГСС. Правда, при дальнейшем увеличении КА относительная масса агрегатов ГСС также возрастает и для очень больших орбитальных станций (значительно превышающих размеры современных) их применение становится малоэффективным. Для очень больших сооружений в космосе будет необходим переход к пассивным методам поддержания ориентации или к поддержанию нужной ориентации путем придания КА вращения (стабилизация вращением). Все это сделает такие станции «неповоротливыми» и заставит вести исследования, требующие многих и разных ориентации с малых КА, лишь базирующихся на такой станции и выполняющих свою основную работу в свободном полете.