ИЗ ИСТОРИИ РЕШЕНИЯ ПРОБЛЕМЫ ФЛАТТЕРА. А.А. БОРИН

УДК 629.7.015.3(091)

В середине 30-х годов советская авиационная техника столкнулась с явлением хотя и известным ранее, но только к этому времени привлекшим к себе пристальное внимание: самолет, построенный по всем правилам инженерной науки того времени, иногда внезапно разрушался в полете при достижении некоторой скорости. Разрушение начиналось с сильной тряски, нарастание которой происходило так быстро, что для принятия каких-либо мер у летчика (например, уменьшения скорости полета) обычно не хватало времени. Это явление получило название флаттера (от англ. flutter - махать, бить крыльями, вибрировать).

Исследования флаттера начались в 1923 г. в Германии (В. Бирнбаум рассмотрел плоскую задачу) [1] и получили значительное развитие в 1929 и следующих годах, когда в Германии и Англии появился ряд работ на эту тему [2 - 8]. Можно отметить два основных направления этих работ: теоретическую основу первого составляли работы, авторы которых пытались получить дифференциальные уравнения колеблющегося крыла, и, интегрируя их, вычислить критическую скорость полета, т. е. скорость, при которой наступает потеря устойчивости конструкции. Кроме упомянутой работы В. Бирнбаума, сюда можно отнести работы Г. Бленка и Либерса [2, 3], М. Раушера [4], экспериментальную работу И. Эссерс [5] и др. Основу второго направления, представленного главным образом работами английских исследователей (Фрейзер и Данкен [6, 7], Локспейсер [8] и др.), составляло изучение физической стороны явления, его энергетического баланса и мер, которыми можно предотвратить его развитие. В упомянутых работах, кроме работы [2], рассматривался преимущественно изгибно-крутильный флаттер крыла, при котором влияние отклонения элерона на характеристики движения предполагалось исключенным.

В Советском Союзе исследования флаттера были начаты в 1932 г. в ЭАО ЦАГИ, где с 1932 по 1935 г. работала бригада по исследованию вибраций, возглавляемая В. П. Лысковым. В конце 1934 - начале 1935 г. работы этой бригады были подвергнуты, резкой критике группой работников ЭАО в составе Е. П. Гроссмана, С. С. Кричевского и А. А. Борина. В мае 1935 г. вышла в свет их работа «К вопросу о потере устойчивости конструкцией крыла в полете» [9], показавшая несостоятельность принятого В. П. Лысковым направления и положившая начало полному выяснению физической сути явления и созданию надежных методов прогнозирования и предупреждения флаттера.

Состояние проблемы к моменту появления этой работы может быть охарактеризовано следующим образом.

A. Физические представления к этому времени дали возможность построить схему энергетического баланса бинарного движения (изгиб-кручение), иллюстрирующую энергообмен как между колеблющимся крылом и внешней средой, так и внутри конструкции крыла между изгибной и крутильной деформациями. Однако, как было показано в упомянутой работе трех авторов, схема нуждалась в значительной доработке. Была обнаружена, но не изучена до конца роль взаимного расположения трех точек - центра жесткости сечения крыла, центра инерции и аэродинамического фокуса.

Б. Построение расчетного метода не было завершено: несмотря на то, что имелись принципиально верные уравнения движения, данные Раушером в работе [4], их интегрирование привело к значениям критических скоростей, которые сильно отличались от соответствующих экспериментальных значений.

B. Рекомендации по борьбе с потерей устойчивости конструкций крыла были разноречивы и нечетки.

* * *

Прежде чем перейти к описанию следующих шагов в исследовании проблемы, изложим вкратце ее существо.

Флаттер относится к категории автоколебаний, г. е. периодическая возмущающая сила возникает в процессе самих колебаний. При флаттере таким возмущающим воздействием являются аэродинамическая сила и момент.

При изгибно-крутильном флаттере крыло совершает маховые движения, в процессе которых периодически изменяются прогиб и угол закручивания каждого сечения крыла. Поскольку крыло колеблется в обдувающем его потоке, эти деформации и вызывают периодическое изменение внешних сил.

Рассматривая сечение крыла на расстоянии z от заделки (рис. 1), разложим его движение на поступательное (изгибное) и вращательное. Для этого введем понятие центра жесткости сечения, т. е. точки, имеющей то свойство, что приложенная к ней сила вызывает деформацию чистого изгиба.

Скорость изгибного движения ду/дτ, складываясь со скоростью набегающего потока V, вызывает изменение местного угла атаки сечения на величину

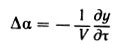
с соответствующим изменением аэродинамической силы и момента на величины:

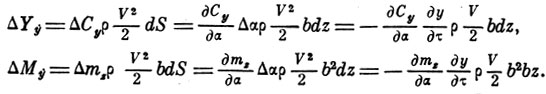
Заметим, что ΔΥ_у всегда является демпфирующим воздействием, так как знак его противоположен знаку ду/дτ. Приращение ΔΜ_у может быть либо возмущающим, либо демпфирующим воздействием в зависимости от взаимного расположения центра жесткости и аэродинамического фокуса.

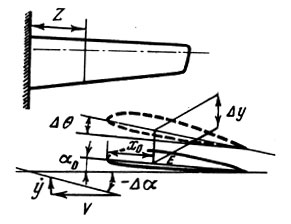
Рис. 1.

Крутильная деформация (которую мы считаем происходящей вокруг центра жесткости) воздействует на аэродинамику двояким образом, изменяя геометрический угол атаки крыла на величину

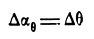
и вызывая изменение угла подхода струй к точкам контура сечения благодаря наличию угловой скорости дО/дх. Элемент, находящийся на расстоянии х от носика профиля, получит вертикальную скорость (рис. 2)

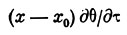
(х₀ - расстояние от носика до центра жесткости) и соответствующее изменение угла подхода струй

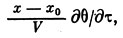
которое изменяется (при дθ/дτ>0) от некоторой отрицательной величины у носика профиля до положительной у его хвостика.

Предполагая, что взаимодействие элемента профиля с внешним потоком определяется местным углом подхода струй, и желая сохранить исходное их направление неизменным, мы должны будем повернуть каждый элемент, как показано на рис. 2. Тем самым мы вводим гипотезу динамической кривизны, заключающуюся в том, что аэродинамическая сила и момент вращающегося профиля равны таковым же неподвижного профиля с кривизной и углом атаки, вычисленными на основании только что изложенных соображений. Приведем без выкладок значение прироста угла атаки

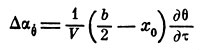
и величины, определяющей аэродинамический эффект кривизны профиля:

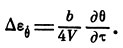
В приведенных рассуждениях негласно фигурирует еще одно важное предположение, называемое гипотезой стационарности, заключающееся в том, что мы пренебрегли влиянием ускорений движения крыла на аэродинамику. Его допустимость оправдывается двумя обстоятельствами: во-первых, небольшой величиной этих ускорений, во-вторых,

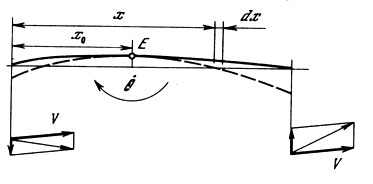
Рис. 2

(и главным образом), тем, что в задаче рассматривается устойчивость равновесного состояния крыла. После начала движения законы, управляющие аэродинамическими силами, могут заметно измениться, но это скажется лишь на развитии явления, но не на условиях его возникновения, в частности не на критической скорости, которая является наиболее важной искомой характеристикой.

Суммируя аэродинамические, упругие и инерционные воздействия, получаем дифференциальные уравнения движения крыла:

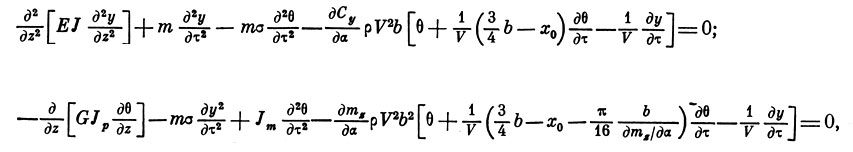
которые являются уравнениями 2-го порядка в частных произведениях. Интегрирование их приводит к характеристическому уравнению - алгебраическому уравнению 4-го порядка, коэффициенты которого являются функциями скорости. Следовательно, функциями скорости являются и критерии устойчивости:

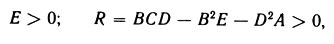
где А, В, С, D, Е - коэффициенты характеристического уравнения.

Равенство нулю критерия Рауса R дает критическую скорость колебательного движения (флаттера), свободного члена Е - апериодического движения - дивергенции.

Дифференциальные уравнения движения в указанном виде впервые были получены еще в 1929 г. Раушером [4]. Уравнения излагаемой работы отличались от уравнений Раушера по существу лишь величиной коэффициента при дθ/дτ в уравнении моментов. Определяя величину этого коэффициента, Раушер исходил из того, что при теоретических значениях дС_у/дα = π и дт₀/дα = π/4 приращение момента относительно середины дужки не зависит от кривизны. Распространяя этот вывод на реальное крыло, для чего нет ни принципиальных, ни экспериментальных предпосылок, Раушер не мог добиться совпадения вычисленных

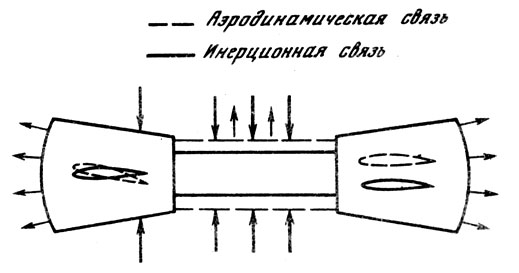
Рис. 3

и фактических критических скоростей. Это впервые удалось достичь в расчетах по предложенным тремя авторами формулам: вычисленные скорости оказывались в регулярном соотношении с опытными, на 5 - 15% ниже последних.

Как уже указывалось выше, в работе трех авторов были также уточнены и дополнены представления английских исследователей о физической стороне проблемы. В этом плане было очень важно уточнение схемы энергетического баланса (рис. 3) и влияние на нее параметров конструкции крыла. Как видно из схемы, приток энергии к крылу совершается через движения кручения и главным образом через связи между движениями кручения и изгиба. Особую роль в характеристике этого процесса играют два параметра, определяющие количество и даже знак подводимой к крылу энергии: 1) взаимное положение центра жесткости и центра инерции; 2) взаимное положение центра жесткости и аэродинамического фокуса.

Совмещение упомянутых выше трех точек приводит к разрыву обеих инерционных связей и аэродинамической связи, передающей энергию от кручения к изгибу. Это приводит к тому, что энергетический цикл разрывается и флаттер становится невозможным.

Как видно из приведенных ранее уравнений, флаттер и дивергенция суть две разные формы одного и того же физического явления - потери устойчивости конструкцией крыла в потоке воздуха, и, следовательно, их аэродинамика в момент начала движения управляется одними и теми же законами. Отсюда вытекает ошибочность вывода Фрейзера и Данкена о существовании некоторой особенной точки - центра независимости, играющей в возникновении периодического движения ту же роль, что аэродинамический фокус в возникновении апериодического движения.

Следовательно, и флаттер, и дивергенция устраняются одновременно совмещением названных трех точек.

В работе [9] было показано, что не имеется необходимости в их точном совмещении: при достаточно близком их расположении возможность флаттера устраняется или по крайней мере критическая скорость становится очень высокой. Было показано также, что критическая скорость дивергенции всегда превышает скорость, при которой наступает статическое перекручивание крыла.

Для проверки разработанной теории был испытан ряд специальных моделей в аэродинамической трубе. Результаты подтвердили надежность теории. В 1935 г. летчиком С. Н. Анохиным была сделана попытка довести до критической скорости флаттера планер с заранее рассчитанным крылом. Однако крыло сломалось на скорости 225 км/ч, которая составляла 75% расчетной критической, и причиной поломки оказалось статическое перекручивание крыла.

Поскольку в реальной конструкции необходимое сближение трех точек далеко не всегда достижимо, то представлял большой интерес анализ конструктивных мероприятий, позволяющих увеличить критическую скорость флаттера. Такой анализ подробно проведен в монографии Е. П. Гроссмана [10]. В ней установлены зависимости, четко отражающие влияние размеров, массовых характеристик крыла и жесткостей его на изгиб и кручение на критическую скорость.

Большинство установленных автором зависимостей было выражено простыми формулами, с большим успехом применявшимися в практике.

В теоретическом плане в работе был дан новый вывод аэродинамических формул для колеблющегося крыла, основанный также на гипотезе стационарности, но без применения гипотезы динамической кривизны. Было установлено наличие сдвига фаз между смещениями различных сечений по размаху крыла, а также между движениями кручения и изгиба.

В другой работе Е. П. Гроссман показал, что сдвиг фаз является обязательным условием вибраций [11].

В 1936 г. М. В. Келдыш в работе [12] подтвердил достоверность формул Раушера, выведенных впервые, как уже указывалось, на основании приближенной теории.

В дальнейшем в рассматриваемый период (до 1941 г.) советскими исследователями был выполнен ряд работ, углубивший и расширивший представления о потере устойчивости различных частей конструкций самолета в полете. Область исследований была расширена работами Е. П. Гроссмана, М. В. Келдыша и Я. М. Пархомовского [13], М. В. Келдыша [14], П. М. Риза [15], Я. М. Пархомовского [16], М. В. Келдыша и Я. М. Пархомовского [17] и др. Существенная важность последней из упомянутых работ состояла в том, что предметом ее рассмотрения была конструктивная схема крыла, широко распространенная не только в то время, но и в наши дни.

В работах П. М. Риза [18] и Л. С. Попова [19] были устранены некоторые допущения, сделанные в более ранних работах (например, абсолютно жесткая заделка крыла), и прослежено влияние этих допущений на критическую скорость.

В заключение отметим, что основным результатом работ, проведенных в СССР в 1934 - 1941 гг., было устранение опасности появления флаттера крыла и оперения; тем самым удалось избежать ограничения роста скоростей самолетов со стороны этого явления.

В частности, удалось:

1. Существенно уточнить представление о механизме возникновения неустойчивости крыла и внести ясность в схему энергетического баланса явления и получить качественные представления о важнейших параметрах, определяющих возникновение флаттера.

2. Получить надежные расчетные формулы для определения критической скорости возникновения флаттера применительно к наиболее часто встречающимся в практике конструктивным схемам крыла и хвостового оперения и для определения скоростей дивергенции и статического перекручивания крыла.

3. Детально изучить влияние ряда конструктивных параметров на критическую скорость возникновения флаттера и разработать эффективные меры борьбы с потерей устойчивости.

4. Разработать методику испытаний на флаттер моделей самолетов и их конструктивных частей в аэродинамических трубах.

ЛИТЕРАТУРА

1. Birnbaum W. Das ebene Problem des schlagenden Flugels. - Z. A. M. M., 1924, S. 277.

2. Blenk H. Liebers. Gekoppelte Biegungs-, Torsions- und Guerruderschwin-gungen von freitragenden und halbjreitragenden Flugeln. - Luftfahrtforschungs., 1929, Bd. 4, H. 3.

3. Blenk H. Liebers. Gekoppelte Torsions- und Biegungsschwinguneen von Tragflugeln. - ZFM, 1925, S. 479.

4. Rauscher M. Uber die Schwingungen freitragender Flugel. - Luftfahrtfor-scung., 1929, Bd. 4, H. 2.

5. Essers J. Untersuchung von Flugelschwingungen in Windkanal. - Luftfahrt-forscung., 1929, Bd. 4, H. 4.

6. Great Britain. Aeronautical research committee: Repts and Memoranda, 1928, N 155.

7. Great Britain. Aeronautical research committee: Repts and Mem., 1931, N 1255.

8. The Journal of Royal Aeronautical Soc., 1933, N 273, p. 783.

9. Гроссман Е. П., Кричевский С. С., Борин А. А. К вопросу о потере устойчивости конструкций крыла в полете. - Труды ЦАГИ, 1935, вып. 202.

10. Гроссман Е. П. Флаттер. - Труды ЦАГИ, 1937, вып. 283.

11. Гроссман Е. П. О причинах флаттера. - Труды ЦАГИ, 1938, вып. 350.

12. Келдыш М. В. Гидродинамический вывод формул Раушера. - Технические заметки ЦАГИ, 1936, № 52.

13. Гроссман Е. П., Келдыш М. В., Пархомовский Я. М. Вибрация крыла с элероном. - Труды ЦАГИ, 1937, вып. 337.

14. Келдыш М. В. Вибрация в воздушном потоке крыла с подкосами. - Труды ЦАГИ, 1938, вып. 357.

15. Риз П. М. Флаттер воздушных винтов. - Труды ЦАГИ, 1938, вып. 391.

16. Пархомовский Я. М. Крутильно-рулевой флаттер хвостового оперения. - Труды ЦАГИ, 1940, вып. 524.

17. Келдыш М. В., Пархомовский Я. М. Колебания крыла с упруго прикрепленным мотором. - Труды ЦАГИ, 1941, вып. 535.

18. Риз П. М. Флаттер крыла с учетом колебаний в направлении наибольшей жесткости. - Труды ЦАГИ, 1937, вып. 340.

19. Попов Л. С. О влиянии фюзеляжа и хвостового оперения на вибрации крыла. - Труды ЦАГИ, 1938, вып. 343.