КОРРЕЛЯЦИОННАЯ МОДЕЛЬ РАЗВИТИЯ ВИДА ТЕХНИКИ. В.П. МИХАЙЛОВ, В.Д. ОНОПРИЕНКО

УДК 608.4(71) +629.735(091)

(Доклад, прочитанный 27 апреля 1973 г. на 174-м заседании Секции истории авиации и космонавтики Советского национального объединения историков естествознания и техники.)

Традиционные методы и средства, используемые в настоящее время в историко-технической науке, не всегда позволяют в полной мере отвечать на поставленные перед ней задачи, так как человек физически не в состоянии переработать большие объемы различной по своему характеру информации, охватить и оценить сложнейшие взаимосвязи между разнообразными техническими, экономическими, политическими и другими явлениями.

Во всех отраслях современной науки происходит интенсивный процесс внедрения математических методов и использования электронно-вычислительной техники. Этот процесс начинает захватывать и историческую и историко-техническую науки. Использование математических методов, математического моделирования и вычислительной техники в исторических исследованиях оказалось весьма эффективным [1, 4, 14].

Математическое моделирование процессов и явлений, а также их изучение на основе математических моделей в настоящее время находят широкое применение в различных областях науки и техники, так как современные наука и техника, изучая качественную сторону процессов и явлений, стремятся выразить их изменения в количественной форме в виде определенных соотношений или пропорций между основными величинами. Математические модели помогают уяснить процессы, происходящие в системах, и предсказать их возможное поведение в различных условиях. Они позволяют вести исследования в аналитическом виде и анализировать различные системы едиными методами, а также распространять действие законов, установленных при помощи модели, на другие отрезки времени.

В настоящее время многие исследователи [1 - 4] используют количественные методы при проведении исторического анализа, однако изучение и исследование развития техники на основе математического моделирования не нашло широкого развития, что можно объяснить, на наш взгляд, отсутствием разработанных методов в этой области. В статье разрабатывается новый (по сравнению с предложенными в работах [1 - 4]) метод исследования развития конкретного вида техники, основные положения которого были изложены авторами ранее [12]. В основу метода положены исследования не косвенных, а прямых (количественных) признаков (По характеру признаки делятся на количественные (выражаемые числами) и атрибутивные, к которым относятся внешний вид, кинематическая структура, цвет окраски и т. д. [11].). Предлагаемый метод количественного анализа не противопоставляется приемам качественного анализа.

Одна из математических моделей, использующая прямые признаки, предложена в 1962 г. в работе В. Ф. Болховитинова [6], который исходил из того факта, что один из основных параметров самолета - вес в значительной мере определяет количественно комплекс его качеств. Предложенная им модель весового уравнения самолетов имела следующий вид:

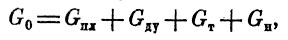
(1)

где G₀, G_nл, G_ду, G_т, G_н соответственно полетный вес самолета, вес планера, вес двигательной установки, вес топлива и вес полезного груза.

В результате простого преобразования выражения (1) - деления обеих частей на G₀ - Болховитиновым было получено уравнение в форме относительных весов:

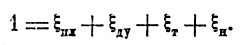
(2)

Это уравнение приемлемо, как показано в работе [6], для анализа и оценки как существующих, так и будущих самолетов. Весовые характеристики самолета в уравнении (2) представлены в относительных коэффициентах полетного веса, что позволяет сравнивать самолеты друг с другом по степени использования единицы массы, как основного элемента совершенства летательного аппарата.

Несмотря на очевидное преимущество анализа развития самолетов при помощи модели Болховитинова, эта модель не позволяет осуществлять сравнительный анализ больше, чем по одному признаку (вес) и не учитывает влияние других важных параметров самолета (скорость полета, мощность двигателей и т. д.), а также их удельной значимости.

В работах Э. Ф. Скороходько [7] и В. Н. Шукова [8] высказаны предположения о необходимости проведения исследований развития технических средств на основе количественного анализа влияния одних признаков на другие, т. е. нахождения корреляционной модели развития техники, причем Шуковым применительно к электромашинам была предложена общая аналитическая запись этой модели

C=f(x,y,z), (3)

где С - целевая функция; х, у, z - конкретные признаки (параметры) электромашин.

В работах [7, 8] выдвигается идея построения корреляционной модели, но не приводится обоснование применения и не указываются методы ее решения. В литературе подробно разработаны методы корреляционной зависимости не более чем для трех переменных [5, 9], что в ряде случаев недостаточно для проведения исследований. При этом изложенные методы, разработанные в основном только для проведения технических исследований, а не историко-технических, имеют следующие основные недостатки:

• - не позволяют устанавливать параметры, значительно влияющие на изучаемое явление, т. е. производить ранжирование;
• - не предусматривают использование быстродействующих вычислительных средств, что ведет к выполнению в каждом конкретном случае большого объема вычислительной работы вручную.

Таким образом, можно констатировать, что в настоящее время существует острая необходимость построения корреляционных моделей конкретных видов технических средств, а также обоснование их применения в историко-технических исследованиях.

Формулировка задачи

Развитие конкретного вида техники целесообразно представить как развитие системы большого масштаба. Вид техники как система большого масштаба - это множество связанных между собой элементов (любой природы), имеющих тот или иной вид упорядоченности по определенным свойствам и связям, а также обладающих относительно, устойчивым единством, которое характеризуется внутренней целостностью, выражающейся в относительной автономности поведения и существования этого множества в системе народного хозяйства страны.

Среди множества признаков и параметров, характеризующих конкретные технические системы или конкретный вид техники (самолет, угледобывающий комбайн и т. д.), существуют такие прямые показатели, как скорость, мощность и т. д., которые для некоторых вопросов изучения могут в известной мере отражать с некоторой точностью развитие отдельного вида техники.

В общем случае если символ С(х) (целевая функция) выразить через некоторое множество признаков, характеризующих конкретный вид техники, то исследование этого вида можно свести к изучению рассматриваемой целевой функции. При этом условимся, что целевая функция С(х) описывается достаточно большим набором признаков П^k_i=1 x_i, где под признаком x_i; понимается некоторая характеристика, относящаяся к изучению конкретного вида техники. В этом случае математическая модель конкретного вида техники может быть представлена следующим уравнением общего вида [12]:

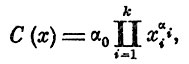
(4)

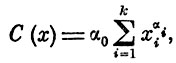
(5)

где С(х) - целевая функция (вес, надежность, стоимость) рассматриваемого вида техники; α₀, α_s, ..., α_i, α_k - коэффициенты корреляции; x₁, х_е, ..., x_i, x_k - основные историко-технические признаки отдельных видов техники.

Построение корреляционной модели

Основная цель при построении корреляционной модели - выявить связь между выборкой целевой функции вида техники и статистической выборкой историко-технических признаков отдельных объектов вида техники (самолетов, автомобилей и т. д.), а также представить эту связь в виде аналитической функции.

При этом метод решения задачи следующий: из статистической выборки историко-технических признаков путем последовательного перебора различного сочетания характерных параметров в уравнении целевой функции

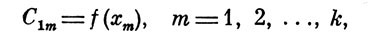
(6)

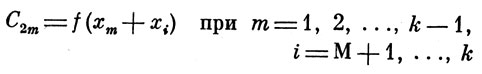
(7)

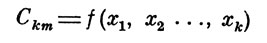
(8)

выбирается такая математическая модель, чтобы комбинация формы аналитической связи и числа характерных признаков обеспечивала бы модель минимально-параметрической размерности при адекватности статистической выборки в заданном интервале надежности.

Практическое решение поставленной задачи осуществляется в шесть последовательных этапов:

• - отбираются основные фактор-аргументы (независимые и зависимые признаки) отдельного вида техники;
• - собираются статистические данные;
• - проверяются эмпирические данные на однородность статистической выборки;
• - принимаются и выбираются аналитические формы связи;
• - разрабатываются алгоритмы решения и описываются в виде программы с целью получения конкретных численных результатов;
• - проводится статистическая оценка и дается историко-техническая интерпретация полученных математических моделей.

После принятия формы связи (4) или (5) решается задача определения неизвестных коэффициентов корреляции следующим путем (для заданных значений признаков).

Исходный статистический материал представляется информационной матрицей

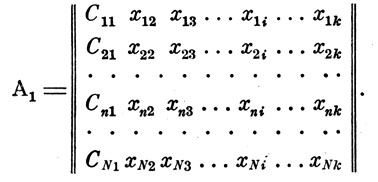
(9)

Строки матрицы представляют собой различные исполнения отдельных видов техники (например, самолетов), а столбцы матрицы - их историко-технические характеристики (полетный вес самолета, максимальная скорость, мощность двигателя и т. д.).

Для решения корреляционной зависимости, представленной выражением (4), приводим это уравнение к линейно-логарифмическому виду

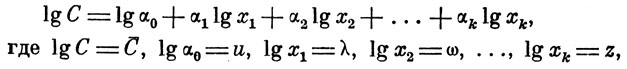
(10)

и тогда уравнение (4) принимает вид

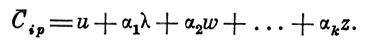
(11)

При этом матрица А₁ (9) преобразуется в матрицу

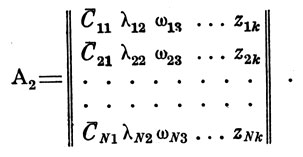
(12)

Далее используем метод наименьших квадратов:

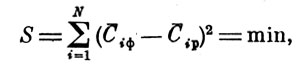
(13)

где N - количество объектов данного вида техники; С^-_iф - фактическое значение целевой функции; С^-_ip - расчетное значение целевой функции.

Подставляя значение С^-_ip из уравнения (11) в уравнение (13), получаем выражение

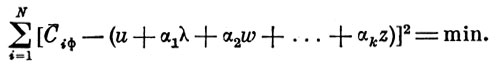
(14)

Определяя частные производные по всем неизвестным и, α₁, α₂, α₃, ..., α_k и приравнивая их нулю, получаем полную систему нормальных уравнений:

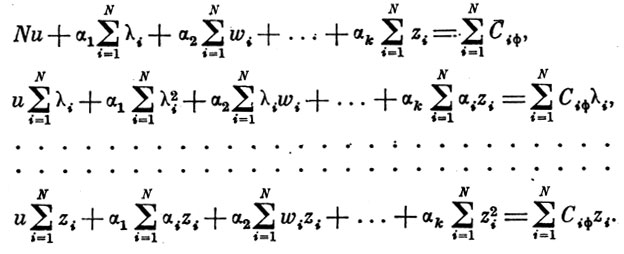
(15)

Решая систему нормальных уравнений (15) методом Гаусса, находим неизвестные величины уравнения и, α₁, α₂,..., α_k и, подставляя их в уравнение (4), искомое уравнение множественной корреляции данного вида техники, пригодность которого как математической модели необходимо еще проверить.

Определяем прежде всего остаточную дисперсию, характеризующую отклонение значений целевой функции относительно найденного уравнения:

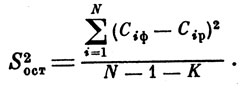
(16)

Дисперсия, характеризующая отклонение результатов расчета, определяется

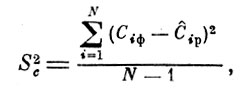
(17)

Для проверки адекватности модели эмпирическим данным строится F - критерий:

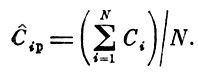
(18)

Удобство использования этого критерия состоит в том, что проверку гипотезы наличия адекватности можно свести к сравнению его с табличным значением.

Если расчетное значение F-критерия больше табличного при заданном значении доверительной вероятности, то модель можно считать адекватной. В противном случае принятую гипотезу приходится отвергать [10]. Табличное значение F определяется по таблицам, составленным Р. Фишером, и зависит только от числа степеней свободы для сравниваемых дисперсий (v₁ = N - 1, v₂ = К - 1) при выбранном значении доверительной вероятности. Комбинированное влияние нескольких параметров на изменение целевой функции определяется коэффициентом множественной корреляции

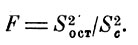
(19)

t=R/σ,

где

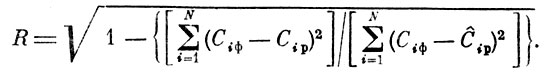
- среднеквадратичная ошибка коэффициента множественной корреляции.

Показатель коэффициента множественной корреляции признается значимым, а связь целевой функции с характерными параметрами - существенной, если расчетное значение t-критерия не меньше критического, определяемого по таблице t-критерия Стьюдента [10] при заданном значении доверительной вероятности и степени свободы.

Для выяснения существенности параметров модели проводят последовательный анализ связи целевой функции с определяющими ее параметрами. С этой целью строятся и оцениваются методами математической статистики модели зависимости целевой функции от каждого историко-технического признака, модели комбинированного влияния на целевую функцию 2, 3, ..., К - 1 историко-технических признаков в различном их сочетании из Л' признаков и общая модель зависимости целевой функции от характерных параметров в целом. Такое исследование является полным и достаточным при определении вклада каждого параметра в исследуемую модель, а также при решении проблемы отсева несущественных историко-технических признаков уравнения.

Алгоритм построения корреляционной модели развития техники реализован в виде программы на языке АЛГОЛ-60. Используя изложенные выше математические преобразования, алгоритм построения и программу построения корреляционной модели в виде выражения (4), определяем численное значение целевой функции С(х).

Корреляционная модель развития самолетов. Проверка возможности прогнозирования

Целью настоящей работы не являлось выяснение всего круга задач, которые могут быть решены изложенным методом. Они формируются, исходя из цели конкретного исследования, наличия и объема статистического материала и возможности применения других, более эффективных методов исследования. Однако отметим, что при помощи изложенного метода возможно решение разнообразных задач по анализу развития конкретного вида техники, что даст возможность количественно установить изменение того или другого параметра и его наиболее существенное влияние на изменение характерной функции, а также степень значимости других параметров. Дифференцирование модели позволит узнать скорость изменения интересующих нас параметров во времени и влияние этих параметров друг на друга. Построение модели для нескольких характерных этапов развития конкретного вида техники или для различных видов даст возможность провести сравнительное исследование их развития и т. д.

В качестве одного из примеров возможного применения изложенного выше метода исследовались зависимости полетного веса самолетов 1913 - 1941 гг. от времени их создания, мощности двигателей, максимальной скорости полета, веса полезной нагрузки, размаха крыльев и их несущей поверхности. С этой целью обработаны статистические данные, взятые из работы [13], основных параметров самолетов с поршневыми двигательными установками, которые и приведены в табл. 1. Отсчет времени взят с 1903 г., с момента первого практического решения проблемы полета человека на аппарате тяжелее воздуха (текущее время Т = 1941 - 1903 = 38).

Основной особенностью программы является исследование влияния каждого из этих параметров на значение полетного веса самолета и комбинированное влияние сочетания двух, трех, четырех и пяти параметров, а также исследование зависимости полетного веса самолета от одновременного действия всех этих факторов. Всего рассматриваются Q сочетаний математических моделей:

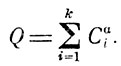
С^α_i-число сочетаний из К независимых параметров; К - число независимых параметров в конкретной модели.

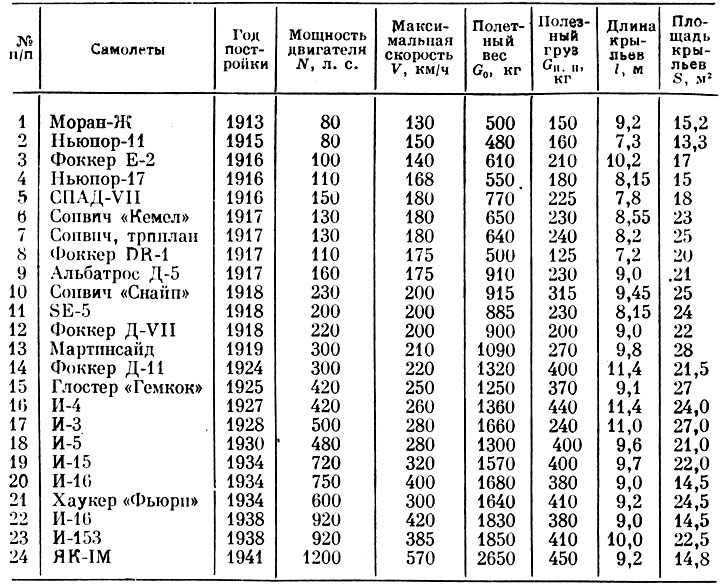
Таблица 1. Характеристики самолетов 1913 - 1941 гг.

В качестве примера решены две следующие задачи:

1. Построение математической модели полетного веса самолета, используя статистические данные всего рассматриваемого периода.

2. Построение математических моделей на основе статистических данных рассматриваемого периода и использование их для задач долгосрочного прогноза.

В первой задаче в качестве искомой зависимости исследовались степенная, показательная и экспоненциальная с целью выявления наиболее предпочтительной формы связи полетного веса самолета. Результаты представлены в табл. 2. Окончательное определение наиболее приемлемой формы связи - в данном случае степенной (формулы (22) и (23)) - производилось на основе личных знаний, опыта и интуиции исследователей.

В качестве одного из примеров возможного применения изложенного выше метода исследовались зависимости полетного веса самолетов 1913 - 1941 гг. от времени их создания, мощности двигателей:

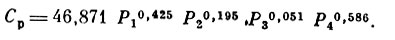
(22)

Модель (22) адекватна эмпирическим данным с доверительной вероятностью 0,95;

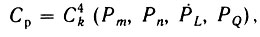
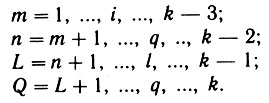
Модель выбрана при i = 1, j = 2, l = 3, q = 4, k = 6.

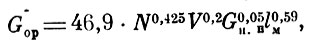
(23)

где G_op - расчетное значение полетного веса самолета, кг; N - мощность двигателя, л. с; V - максимальная скорость полета, км/с; G_n.н - вес полезной нагрузки, кг; l_м - длина крыльев, м.

Сравнение фактических данных С_ф, взятых из табл. 1, и. расчетных С_р, полученных на основе формулы (23) (табл. 2), показывает достаточно хорошее совпадение этих величин.

Это позволяет утверждать, что формула (23) является математической моделью полетного веса самолетов, приведеных в табл. 1.

Вторая задача - определение долгосрочного прогноза полетного веса самолета по его характерным параметрам - заключалась в использовании математических моделей, построенных на основе статистических данных одного этапа развития конкретного вида техники, и в экстраполяции этой модели на другой этап. Так, в настоящей работе (с целью определения возможности использования корреляционной модели в задачах инженерного прогноза) математические модели, построенные по данным характеристик самолетов периода 1913 - 1918 гг. экстраполировались на период 1919 - 1941 гг. Данные, полученные на основе экстраполяции, сравнивались с заранее известными фактическими значениями полетного веса самолета (кривая G_0ф). Фактические данные брались на основе табл. 1. Величина расхождения кривых С₀ прогноз и G_0ф - являлась мерой, определяющей пригодность данного метода для проведения прогнозирования.

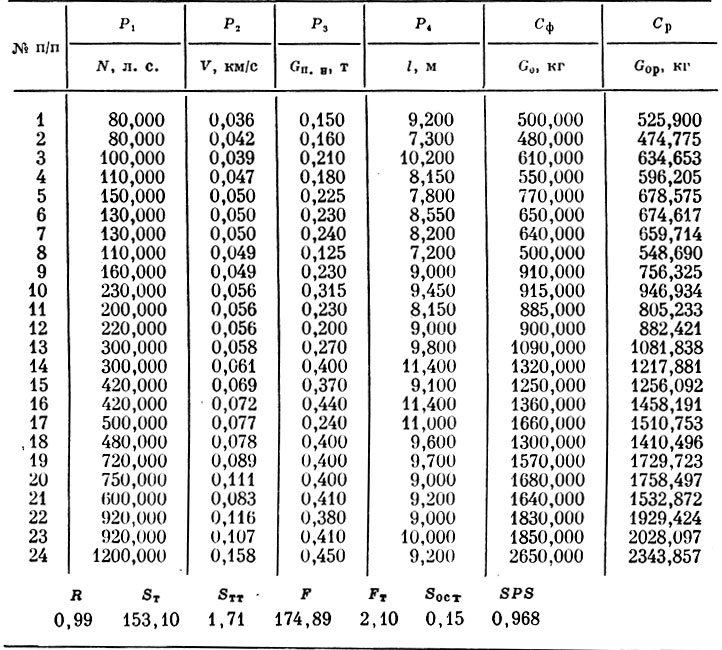
По статистическим данным за период 1913 - 1918 гг. строились математические модели зависимости полетного веса от одного, двух трех, четырех, пяти и шести параметров. Для проведения дальнейших исследований из каждого разряда моделей выбиралась одна, обладающая свойством адекватности и имеющая наибольший коэффициент множественной корреляции (0,95<1) и наименьшую относительную ошибку. Расчеты показали, что математические модели зависимости целевой функции от одного из характерных параметров перечисленным выше требованиям не удовлетворяли и в задаче прогнозирования не рассматривались. Для прогнозирования выбраны следующие математические модели (>Для проведения прогнозирования должны быть известны значения величин N, V, Gп.н и т. д. по времени. В настоящей работе не ставилась задача разработки способов определения этих величин (в примере они брались на основании статистики 1919-1941 гг.). Однако укажем на некоторые способы: 1) применение метода экспертных оценок; 2) возможно построение этих величин на основе подобной корреляционной модели, в которых целевыми функциями будут выступать искомые величины, например N = αGα1двN-α2, где Gдв, N, γ - соответственно вес двигателя, количество цилиндров, расход топлива и т. д. В конечном счете получим систему уравнении G=f(N,V,Gsub>п.н , ...); N = f(Gдв, n, γ ...) и т. д.). ):

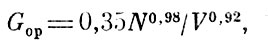
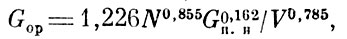
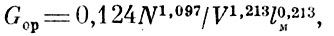
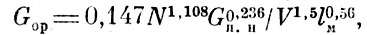
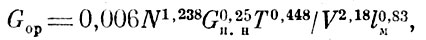
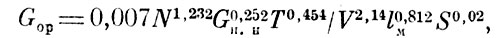
где G_op - расчетное значение полетного веса самолета, кг; N - мощность двигателя, л. с; V - максимальная скорость полета, км/с; G_п.н - вес полезной нагрузки, кг; l_м - размах крыльев, м; S - несущая поверхность крыльев, м; Т - время, годы.

Исследования показали, что в начале расчетов определяются один-два доминирующих параметра, которые являются основными и в последующих моделях. Если добавление к этим параметрам последовательно по одному из других параметров сначала до четырех приводит к улучшению модели прогнозирования, то дальнейшее усложнение моделиза счет увеличения параметров приводит вследствие их автокорреляции к ухудшению точности прогнозирования.

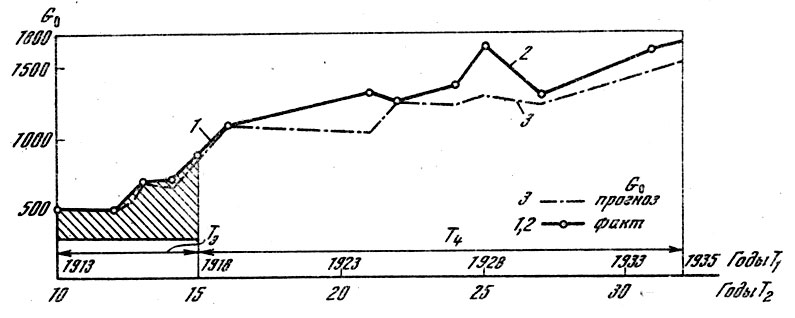
Зависимость полетного веса самолета от мощности двигателя, веса полезной нагрузки, максимальной скорости полета и размаха крыльев

Т₁ - текущее календарное время, годы; Т₂ - фактическое время развития конкретною вида техники (самолетов), начало отсчета - первый полет человека на самолете - 1903 г.; Т₃ - интервал обрабатываемых статистических данных для нахождения математической модели развития техники: Т₄ - интервал прогноза, полученного на основе математической модели по статистическим данным интервала Т₃. 1 - фактические данные интервала Т₃ (1913 - 1918), взятые на основании табл. 1; 2 - фактические данные интервала Т₄ (1919 - 1941), взятые на основании табл. 1. для проведения сравнения с результатами прогноза; 3 - прогноз развития вида техники (самолетов) для интервала Т₄, (1919 - 1941), полученный с помощью математической модели (27).

Результаты долгосрочных прогнозов на основе наиболее точной четырехпараметровой модели (27) приведены на рисунке, из которого видно, что разработанный метод обеспечивает удовлетворительную точность прогноза на участке, равном приблизительно четырем интервалам исходного. Однако по сравнению с 70-летним исходным интервалом развития авиационной техники (1903 - 1973 гг.) интервал прогнозирования на ближайшие 5 - 15 лет не превышает значения 0,2 исходного. На таком интервале, как видно на рис. 1, точность прогноза значительно повышается.

Заключение

1. Разработанный метод построения математической модели развития конкретного вида техники позволяет определить закономерность развития с учетом основных параметров изучаемого вида техники.

2. Полученная модель позволяет осуществлять прогнозирование основных параметров конкретного вида техники на достаточно большом интервале. С ее помощью возможно установление закономерности развития конкретного вида техники с заданной точностью.

3. Разработанный метод позволяет установить и выбрать наиболее приемлемую математическую форму связи закономерности развития конкретного вида техники (линейную, степенную, показательную или экспоненциальную), выделить основные технические характеристики исследуемою процесса, а также произвести ранжирование его параметров.

4. Применительно к изучению развития самолетов с поршневыми двигательными установками наибольшая точность (не менее 92%) прогноза получается при построении математической модели степенного вида в зависимости от четырех параметров (мощности двигательной установки, веса полезной нагрузки, скорости полета и величины размаха крыльев самолета). Причем наибольшее влияние, как это видно из уравнений (25) - (29), имеет скорость полета.

ЛИТЕРАТУРА

1. Кохно Д. В., Г. М., Ю. Ю., Ковальченко Н. Д., Палли К. Е., Устинов В. А. Количественные и машинные методы обработки исторической информации. - Новая и новейшая история, 1970, № 5, с. 28 - 36.

2. Смирнов Л. П. Разработка метода анализа развития конкретных технических средств (на примере угледобывающих комбайнов): Канд. дис. М.: ИИЕиТ АН СССР, 1966.

3. Rashevsky N. Outline of mathematical approach to history. - Bull. Math. Biophys., 1953, vol. 15, p. 197 - 234.

4. Устинов В. А. Применение математических машин в исторической науке. М., 1964.

5. Конончук И. И. Методы оценки выносливости жаропрочных сплавов. М., 1966, с. 130 - 132.

6. Болховитинов В. Ф. Пути развития летательных аппаратов. М., 1962.

7. Скороходько Э. Ф. Выявление корреляционных связей между признаками с помощью ЭЦВМ. - В кн.: Применение электронно-вычислительных устройств в исследованиях по истории науки и техники. М., 1966.

8. Шуков В. Н. Некоторые вопросы прогнозирования совершенствования параметров машин. - Тр. Ленингр. политехн. ин-та, 1969, № 306, с. 60 - 65.

9. Длин А. М. Математическая статистика. М., 1951, с. 253 - 256.

10. Адамович Л. П. Рациональные приемы составления аналитических прописей. Харьков, 1966, с. 55.

11. Лукомский Я. И. Теории корреляции и ее применение к анализу производства. М., 1961, с. 5.

12. Михайлов В. П., Оноприенко В. Д. К вопросу применения математических методов в исследованиях по развитию техники. - В кн.: Материалы по истории техники: XIII Междунар. конгр. по истории науки. М., 1971, с. 20 - 21.

13. Пышное В. С. Из истории летательных аппаратов. М., 1968, с. 96 - 101.

14. Математические методы в исторических исследованиях. М., 1972.