Гравитационные силы

Как указывалось, гравитационные силы (или силы тяготения) в громадном большинстве случаев целиком определяют свободное движение космического аппарата. Гравитационные силы определяются законом всемирного тяготения: всякое точечное материальное тело притягивает каждое другое точечное материальное тело с силой, пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними. Честь открытия закона всемирного тяготения принадлежит знаменитому английскому ученому - математику, физику и астроному Исааку Ньютону (1643 - 1727).

Говорят, что открытие Ньютоном великого закона объясняется случайностью. Якобы произошло это примерно так: молодой 23-летний ученый, погруженный в глубокое раздумье, сидел в саду и, наблюдая падение с дерева яблок, пришел к мысли, что тяготение есть мировая сила. Так ли это было на самом деле - трудно сказать. Однако можно наверняка утверждать, что о силе тяжести люди знали и до Ньютона. Вполне возможно, что изучение сил тяготения началось еще с того знаменательного времени, когда Ева вкусила яблоко в райском саду.

В своей количественной интерпретации закон всемирного тяготения записывается чрезвычайно просто:

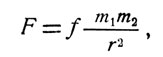
(1)

где F - сила, с которой притягиваются две материальные точки, имеющие массы m₁, m₂ соответственно, r - расстояние между точками, f - гравитационная постоянная, равная 6,668 х 10^-8 см³/гхсек². Гравитационная постоянная численно равна величине силы, с которой притягиваются две материальные точки, имеющие массу 1 г каждая и расположенные на расстоянии 1 см.

Пользуясь этой формулой, вычислить силу притяжения двух тел конечных размеров, казалось бы, очень просто. Для этого достаточно каждое тело разделить на отдельные точки, затем найти силы притяжения каждой точкой одного тела и каждой точкой другого тела и после этого определить равнодействующую всех элементарных сил. Такой путь очевиден, но не так-то прост. Действительно, формула (1) в своем непосредственном представлении имеет смысл только для масс, сосредоточенных в точке. Но точка, по математическому определению, не имеет размеров. Значит, как бы мы ни делили данное тело на сколь угодно малые части, все равно не удастся получить точку, и поэтому мы не вправе применять для вычисления-силы притяжения такую простую формулу. Однако математики нашли выход из такого, на первый взгляд, безвыходного положения. Для того чтобы вычислить силу притяжения, они вначале разделяют все тело на отдельные элементарные части, например, кубики, и считают условно, что масса каждого из кубиков сосредоточена в его центре и из этого условия применяют формулу (1) для нахождения сил притяжения. После этого, написав формулу для равнодействующей всех элементарных сил, они пользуются предельным переходом, сводя объем каждого кубика к нулю (к точке), а число таких кубиков соответственно увеличивают безгранично (математики говорят - устремляют в бесконечность). В результате равнодействующая получается как сумма бесконечно малых сил, число которых бесконечно.

Отвлекаясь от рассматриваемой задачи, следует сказать, что описанный прием, состоящий в том, что какой-либо объем или протекающий процесс разбивается на бесконечно малые составляющие, которые в последующем суммируются, составляет существо большого раздела математики, называемого дифференциальным и интегральным исчислением. В настоящее время невозможно найти область науки и техники, где бы не применялся математический аппарат дифференциального и интегрального исчислений, и поэтому знание его и умение оперировать им так же уверенно, как мы оперируем сложением и вычитанием, умножением и делением, возведением в степень и извлечением корня, является неотъемлемой частью знаний всякого специалиста. Этот математический аппарат позволил существенным образом упростить и облегчить процесс вычисления сил притяжения и получить ряд практически важных выводов. Вот некоторые из них, которые широко используются в небесной механике и космической баллистике:

1. Сферическое тело (шар), плотность которого является постоянной по всему объему, притягивает всякое другое расположенное вне его тело так, как если бы вся его масса была сосредоточена в центре сферы. Это, в частности, означает, что для вычисления силы притяжения двух шариков уже нет необходимости разделять их на элементарные объемы, как это было описано выше, а можно просто воспользоваться формулой (1), в которой m₁, m₂ есть массы этих шариков, а r - расстояние между их центрами. Далее, если принять, что наша Земля есть шар (хотя в действительности это не совсем так), то для вычисления силы притяжения ею всякого другого тела можно положить (без всяких допущений!), что вся ее масса сосредоточена в центре. В этом случае баллистики говорят, что гравитационное поле является центральным, т. е. сила притяжения всегда направлена к центру Земли.

2. Если плотность тела имеет центральную сферическую симметрию, то оно (тело) притягивает всякое иное тело так, как будто вся масса его сосредоточена в точке симметрии. Отсюда следует, что пустотелый шар (наподобие детского мяча) или вложенные друг в друга различные шары (как куклы-матрешки) с совпадающими центрами притягивают другие внешние тела, как материальная точка, имеющая массу шара (или шаров), расположенная в центре его.

Необходимо отметить одно любопытное следствие, вытекающее из свойств притяжения пустотелого шара. Оказывается, что если какое-либо тело поместить внутрь шара - в центр или на внутреннюю оболочку или же где-то в промежуточном положении, то сумма всех сил притяжения, действующих на него со стороны оболочки, всегда будет равна нулю. Иными словами, это тело будет находиться в состоянии невесомости и, если вы окажетесь рядом с ним, вы уподобитесь космонавту, только для этого уже не надо лететь с космическими скоростями. Если вы оттолкнетесь от оболочки, то совершенно свободно долетите до ее противоположной стороны точно с такой же скоростью, с какой вы оттолкнулись.

И еще одно замечание. При опускании в глубь Земли (например, в шахту) ваш вес будет уменьшаться. Действительно, если вы опуститесь на некоторую глубину внутрь Земли, то тот шаровой слой Земли, который расположен выше вас, не будет, участвовать в создании веса, а вес образуется лишь той частью Земли, которая расположена ниже вас. Но это ведь уже только часть Земли и, значит, ее притяжение, т. е. ваш вес, станет меньше. Если представить, что вы достигли центра Земли, то здесь вы уже окажетесь в состоянии невесомости.

Значит, если у вас возникает желание ощутить невесомость, то для этой цели не обязательно лететь в космос. Попробуйте "всего-навсего" забраться в центр нашей Земли. Расчеты показывают, что при опускании в шахту на каждые 100 м вы будете "терять в весе" около 4 г.

Незнание законов притяжения или их неправильное истолкование может привести к курьезам. Вы, конечно, читали очень занимательную научно-фантастическую повесть В. А. Обручева "Плутония". В ней описывается, что некая экспедиция где-то в акватории Северного Ледовитого океана случайно обнаружила вход во внутреннюю часть Земли. Оказалось, что Земля внутри пуста и представляет собой нечто вроде футбольного мяча. Внутри Земли экспедиция обнаружила доисторический мир, первобытную природу, животных и даже людей. Там тоже были реки, озера, моря, горы, пустыни - словом, все, что есть на наружной поверхности Земли. Только жизнь протекала с некоторым сдвигом назад во времени.

Прочитав только что написанное о свойствах притяжения шарового слоя, вы сразу же воскликнете: как же там могли ходить люди, животные, течь реки, если все они находились в состоянии невесомости? Попытаясь шагнуть, оттолкнувшись от Земли, человек неминуемо должен взлететь, после чего, уподобляясь птице, начнет свободно плавать внутри Земли!

Мало того, в этой же книге пишется, что внутри Земли было тоже какое-то светило, подобное Солнцу, которое плавало где-то в районе центра Земли (кстати, что его удерживало там?). Это светило притягивало к себе и оболочку Земли, и все-все предметы, расположенные на ее внутренней поверхности. И так как все предметы, лежащие на этой поверхности, люди, звери, вода не были как-то прикреплены к Земле, то они под влиянием сил притяжения внутреннего "солнца" должны были обязательно полететь к центру Земли. Вот вам и путешествие! Правда, если закрыть глаза на это досадное недоразумение, то книга читается с несомненным интересом. И мы ни в коей мере не упрекаем уважаемого Владимира Афанасьевича в незнании законов тяготения.

Сделаем одну оговорку. Все происходило бы именно так, как описано в книге, но только в том случае, если бы Земля не вращалась. За счет вращения Земли и с нею всех предметов возникают центробежные силы, стремящиеся разорвать Землю на части, оторвать от нее все предметы и выбросить их в космос. Значит люди, находящиеся внутри Земли, центробежной силой прижимаются к ее поверхности.

Центробежная сила действует в направлении, перпендикулярном оси вращения Земли. Если человек находится на экваторе (рис. 2, положение а), то эта сила будет действовать в точности через голову к ногам и он будет ощущать ее как увеличение веса. Когда же юн займет другое положение (б), то указанная сила будет стремиться свалить человека набок и "утащить" к экватору. Наконец, при нахождении в полюсах (положение в) центробежная сила будет отсутствовать и здесь будет наблюдаться состояние невесомости. За счет этих сил реки должны потечь от полюсов к экватору и в районе экватора широкой лентой образуется океан, опоясывающий всю внутреннюю часть Земли.

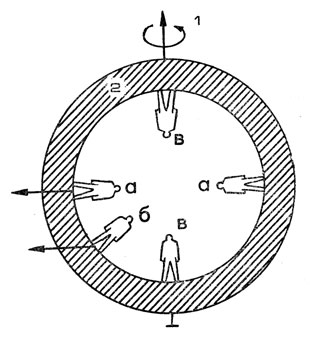
Рис. 2. Схема действия центробежных сил на человека, стоящего внутри Земли: 1 - ось вращения Земли; 2 - поперечный разрез Земли

Эти же эффекты должны наблюдаться при рассмотрении течения рек и на внешней поверхности Земли. Однако нам известно, что реки на Земле текут во все стороны света - и в направлении к северу, и к югу, и на запад, и на восток. Выходит, что центробежная сила не влияет? Но ведь она существует! Тогда в чем дело? Ответить на этот вопрос не просто и поэтому его рассмотрим несколько позже.

Возвращаясь же к экспедиции из "Плутонии", укажем лишь, что она вошла во внутреннюю часть Земли в районе Северного полюса, т. е. в том районе, где центробежные силы чрезвычайно малы. Поэтому отважные путешественники едва ли могли бы сделать и один шаг, как оторвались от Земли. В этом состоит одно из недоразумений "Плутонии".

Но вернемся из недр Земли в космос. В практических расчетах полетов космических аппаратов баллистикам часто бывает значительно удобнее оперировать не с величинами сил притяжения, а с ускорениями, создаваемыми этими силами. Действительно, второй закон Ньютона гласит, что сила притяжения измеряется произведением массы m на сообщенное ей ускорение g, т. е.

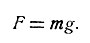
Если под величиной т понимать массу космического аппарата, а под m3 - массу Земли, то, используя формулу (1), определим

где r - расстояние от центра Земли до космического аппарата. Полученная формула выглядит несколько проще, чем формула 1, поскольку здесь исчезла одна из масс, а именно масса космического аппарата. Значит, этой формулой можно пользоваться для вычисления величины ускорения, воздействующего на космический аппарат и направленного к центру Земли, совершенно забывая и даже не зная действительной массы космического аппарата. Произведение двух известных величин fm3 носит название гравитационного параметра Земли (или какой-либо другой планеты) и часто обозначается буквой b₀. Численные значения этого параметра для планет Солнечной системы и Луны, а также радиусы планет и ускорения силы тяжести на их поверхности даны в табл. 1.

Таким образом, формула для определения ускорения силы тяжести принимает следующий простой вид:

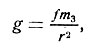
(2)

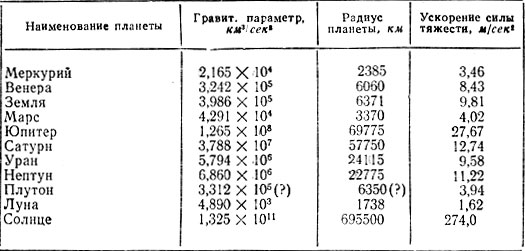
Таблица 1. Некоторые характеристики планет и Луны

Если бы космический аппарат летел непосредственно у поверхности Земли, то его ускорение составляло бы 9,81 м/сек². По мере увеличения высоты полета (т. е. величины r) в соответствии с полученной формулой величина ускорения будет уменьшаться. Так, если радиус орбиты увеличится в два раза по сравнению с радиусом поверхности Земли, то ускорение силы тяжести уменьшится уже в четыре раза и составит около 2,5 м/сек². На расстоянии до Луны (r = 400 000 км) земное ускорение будет равно лишь 1,36 мм/сек².