Почему не произошло мировой катастрофы, или для чего нужно полярное сжатие Земли?

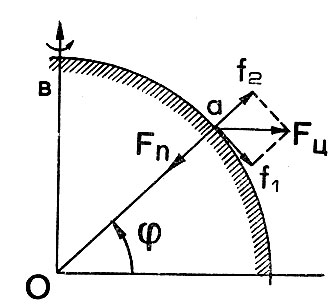
Рис. 3. Схема действия сил на тело а, расположенное на поверхности Земли

Вернемся к предыдущему параграфу, именно к той его части, где речь шла о центробежных силах, и рассмотрим этот вопрос более подробно. Вначале предположим, что Земля представляет собой шар и, следовательно, притягивает любое тело в направлении к своему центру. На рис. 3 показана часть поверхности Земли, ось вращения Земли Ob и центр Земли О. Рассмотрим действие сил на некоторый предмет, расположенный в точке а на поверхности Земли. Прежде всего на этот .предмет действует сила притяжения Земли f_п, направленная к центру Земли и равная, согласно формуле (1),

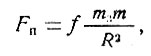
где m3 - масса Земли, m - масса взятого нами предмета (точки), r - радиус Земли. Далее, на этот же предмет действует центробежная сила fц, направленная по перпендикуляру к оси вращения Земли. Величина этой силы зависит от массы предмета, угловой скорости вращения Земли и расстояния точки а от оси вращения Земли. Наибольшее значение центробежная сила будет иметь на экваторе и при весе предмета 100 кг будет равна 0,34 кг. С такой силой Земля стремится отбросить взятый предмет в космос, тогда как сила тяготения, равная 100 кг, удерживает его на Земле. Каждый член экспедиции,из упоминавшейся книги "Плутония", если бы он находился на экваторе и весил в нормальной обстановке 100 кг, дополнительно прижимался бы к Земле с силой 0,34 кг. Конечно, эта сила сравнительно мала, но ее все же можно легко измерить.

Действие силы fц на точку а (рис. 3) разложим на два направления: вдоль радиуса (сила f₂) и по касательной к горизонту (сила f₁). Сила f₂ как бы уменьшает вес тела, а сила f₁ старается сдвинуть его к экватору. Касательная сила f₁ на экваторе и на полюсах отсутствует, а при нахождении рассматриваемой точки в любом другом положении она всегда действует по направлению к экватору. Наибольшего значения она достигает на 45° северной или южной широты и составляет половину центробежной силы на экваторе. При весе груза 100 кг она будет равна 0,17 кг.

Не следует забывать, что эта сила действует на каждый предмет, на каждую частицу его, действует одновременно и постоянно до тех пор, пока существует вращение Земли. Например, твердый металлический шарик, положенный на стеклянную горизонтальную поверхность, покатился бы вдоль меридиана по направлению к экватору; груз, подвешенный на гибкой нити, тоже бы отклонился в ту же сторону. Давайте теперь на мгновение представим, что Земля имеет сферическую форму. В результате действия центробежной силы вся вода должна скатываться от полюсов к экватору, реки должны также течь в этом же направлении. Земля в направлении от экватора к полюсам будет обезвоживаться, превратится в безжизненную пустыню. В то же время в районе экватора, как мы уже говорили, широким поясом, охватывающим всю Землю, должен разлиться глубоководный океан. Этот океан затопит многочисленные острова и материки, расположенные в районе экватора, экзотический Египет и Мексику; Греция и Италия, вся северная часть Африки и много-много других областей окажутся под водой; холодная вода, стекающая с полюсов, охладит теплые океаны, что приведет к гибели тепловодных морских обитателей. Словом, условия жизни на Земле резко изменятся и это обстоятельство по праву можно было бы назвать мировой катастрофой. Однако этого мы почему-то не наблюдаем. Реки, как и испокон веков, текут во всех направлениях, а не только к экватору; в районе полюсов сосредоточены громадные массы воды и она совсем не проявляет тенденции перемещаться в экваториальные области. Мало того, нам даже известны громадные течения воды с экватора на север, как, например, течение Гольфстрим. Это обстоятельство наводит на мысль, что Земля, по-видимому, не является шаром, и что гравитационное поле ее, следовательно, также не является центральным, а имеет гораздо более сложную структуру. Поэтому давайте качественно установим необходимую форму Земли, чтобы не произошло описанной мировой катастрофы.

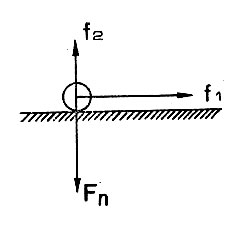
Рис. 4. Схема действия сил на шарик, расположенный на горизонтальной плоскости

Пусть на поверхности Земли находится шарик (рис. 4), который без трения может катиться в любую сторону. (Вместо шарика можно рассматривать любую частичку воды, и так как вся вода движется одновременно, то можно условно считать, что каждая ее частица словно бы катится наподобие шарика). На этот шарик действует сила тяготения f_п Земли и центробежная сила f₂, составляющая которой f₂ уменьшает действие силы притяжения, а составляющая f₁ вызывает смещение шарика по линии ее действия. Иначе говоря, шарик должен покатиться вдоль направления этой силы. Что же необходимо сделать, чтобы шарик не покатился? Предположим, что в том месте, где расположен наш шарик, поверхность Земли слегка повышается в направлении к экватору и составляет с местным горизонтом угол β (рис. 5). В этом случае составляющая силы притяжения F′_ц направленная параллельно новой поверхности Земли, будет противодействовать силе f₁. Величина силы F′_п зависит от угла β и поэтому можно всегда подобрать такое значение угла повышения местности, когда шарик будет находиться в покое. Значит, чтобы шарик находился в равновесии, он всегда в направлении к экватору должен как бы видеть повышение местности. Это повышение, измеряемое углом, будет наибольшим там, где сила f₁ максимальна, т. е. на средних широтах. Наименьшее повышение местности должно быть в районе полюсов и экватора, где действие силы f₁ минимально. Этому условию отвечает так называемое сжатие Земли (т. е. Земля сжата с полюсов). Действительность подтвердила эту гипотезу о сжатии Земли. Земля: действительно сжата в направлении полюсов.

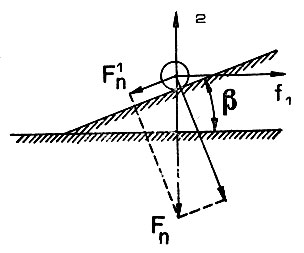
Рис. 5. Схема действия сил на шарик, расположенный на наклонной плоскости

Сжатие - это хорошо известный баллистикам научный термин. Когда говорят, что Земля сжата, то это вызывает совершенно правильную ассоциацию: гигантские руки как бы взяли и сжали Землю с полюсов и раздавили ее как ком пластилина. Схематический вид сжатой Земли показан на рис. 6. Правда, величина сжатия относительно невелика: в районе полюсов поверхность сжатой Земли отстоит от сферической всего на 21 км, и при среднем радиусе Земли 6370 км такое сжатие трудно изобразить на приведенном рисунке. Сжатие возникло не по чьему-то доброму желанию, оно есть следствие вращения Земли. Всю нашу Землю можно представить как некоторую жидкую сферу. Действительно, как утверждают геофизики, вся внутренняя часть Земли представляет собой расплавленную жидкую массу, которая снаружи окружена плотной корой. За счет вращения Земли эта жидкая масса стремится из шара превратиться в "лепешку", но этому препятствуют силы тяготения. Наступает некоторое динамическое равновесие, которому автоматически соответствует достаточно близкая к наблюдаемой нами фигура сжатой у полюсов Земли.

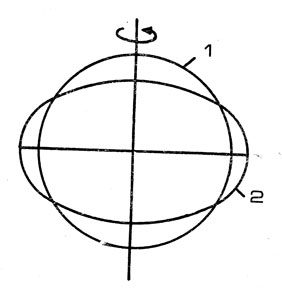
Рис. 6. Поперечный разрез сферической (1) и сжатой (2) Земли

Таким образом, сжатие Земли выручило нас от той неизбежной катастрофы, о которой мы уже говорили. Природа мудра - она даже в космическом масштабе позаботилась о создании для всего живого на Земле наиболее благоприятных условий. Но баллистикам по их специфике работы от этого отнюдь не стало легче, а наоборот труднее, поскольку поле Земли перестало быть центральным и значительно усложнилось.

Оценим теперь величины углов упомянутого повышения горизонта в зависимости от широты местоположения шарика.

Расчеты показывают, что наибольшее значение угол β достигает на широте 45° и равен менее ОД градуса. На всех остальных широтах угол β будет еще меньше. Чтобы построить такую наклонную плоскость, необходимо один край ее положить у ваших ног, а другой поднять над сферической Землей в одном километре от вас на выcоту около 1,6 м. Математиками получено аналитическое выражение для величины радиуса сжатой Земли в зависимости от широты рассматриваемой точки. Выражение это имеет очень простой вид:

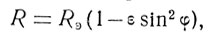
где Rэ - экваториальный радиус Земли, ε - безразмерный коэффициент, называемый сжатием Земли.

Таким образом, начав с гипотезы о сферической форме Земли, мы, не производя специальных экспериментов, с помощью рассуждений доказали, что Земля обязательно должна быть сжатой.

Геодезисты пошли дальше. Они ввели новое понятие для формы Земли, определив ее фигуру. Фигурой Земли называют уровенную поверхность силы тяжести. Это такая поверхность, силы притяжения в любой точке которой одинаковы. Она совпадает с океанами в некотором среднем их состоянии при отсутствии возмущений от атмосферного давления, приливов и других факторов; тело, ограниченное этой уровенной поверхностью силы тяжести, называют геоидом. Термины "фигура Земли", "геоид" часто встречаются в серьезных исследованиях и популярной литературе. Мы тоже не обойдемся без них.

Полных сведений о форме и размерах геоида в настоящее время нет. В качестве последовательных приближений к геоиду принимают сферу, сфероид и трехосный эллипсоид. Каждое из этих тел можно принять за тело отсчета (фигуру относимости, как говорят геодезисты) при определении положений отдельных точек геоида.

Установлено, что геоид незначительно отличается от сфероида. Сфероидом называют тело, полученное вращением эллипса вокруг его малой оси. Величина, равная

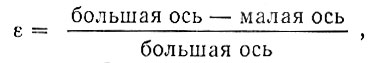
носит название сжатия Земли. Численное значение ее примерно равно 1/298, т. е. полярный диаметр Земли на одну 298-ю часть (примерно на 0,3%) короче экваториального диаметра.

Первая численная оценка величины сжатия Земли была выполнена Ньютоном, хотя наличие сжатия Земли было открыто несколько раньше его. В 1672 году руководитель французской экспедиции в Южную Америку Жак Рише заметил, что маятниковые часы, хорошо идущие в Париже, вдруг стали отставать на 2,5 минуты в сутки в Кайенне. Но определить по этим данным, насколько Земля отличается от сферы, до открытия закона тяготения было, разумеется, невозможно. Ньютоновская идея определения величины сжатия Земли состояла в следующем. Представим себе трубу с водой, идущую из полюса Земли до ее центра, и такую же трубу, направленную от центра Земли в какую-либо точку экватора. Давление воды в каждой из этих труб в центре Земли должно быть одинаковым, так как вода в целом на Земле не перетекает от полюсов к экватору или наоборот. Но в экваториальном канале за счет вращения Земли центробежный эффект несколько уменьшает давление и, следовательно, он должен быть несколько длиннее. Выполнив необходимые расчеты, Ньютон получил для сжатия величину 1/230, и в течение почти столетия его оценка оставалась лучшей и наиболее обоснованной.

Таблица 2. Сжатие Земли

Экспериментальное определение величины сжатия Земли продолжалось долгие годы и оно не закончено и сейчас. Этим вопросом занимались Кассини и его сын, экспедиция Мопертюи, перуанская экспедиция и другие. Использовались различные методы, основанные на измерении длин дуг меридианов и измерении силы тяжести во всех уголках Земли. Приводимая табл. 2 дает наглядное представление о последовательности уточнения фигуры Земли и, глядя на нее, мы можем только гадать о тех трудностях и трудоемкости работ, которые предшествовали получению одного, казалось бы, очень незаметного числа, характеризующего фигуру Земли.

Быстрое уточнение фигуры Земли началось с момента запуска искусственных спутников Земли. Оказалось, что, изучая эволюцию орбит спутников, можно достаточно надежно (конечно, по сравнению с предшествующими до этого методами) определить величину сжатия Земли. По сообщению американских исследователей в течение года с момента запуска первых спутников получена новая величина для сжатия: она заключалась между 1/298,2 и 1/298,3 и значительно отличалась от предшествующей величины 1/297,1. Согласно старой оценке (до запуска спутника) экваториальный диаметр Земли превышал полярный на 42,94 км, а по повой - на 42,77 км. При этом экваториальный диаметр оказался равным 12756,33 км., а полярный - 12713,56 км.

Разумеется, стоимость билета на самолет не изменится из-за того, что расстояние между полюсами увеличилось на 170 м, а длина маршрута от экватора к полюсу возросла на 0,5 км! Однако эти результаты имели чрезвычайно важное значение для геодезистов, которые производили измерения с точностью до 10 м и поэтому были огорчены, когда узнали, что работали с искаженной моделью Земли. Точно так же возникли новые заботы и у геофизиков, так как прежние представления о жидком строении внутренней части Земли перестали согласовываться с новой оценкой сжатия.

В заключение укажем, что в Советском Союзе в качестве тела относимого принят земной сфероид Ф. Н. Красовского, большая полуось которого (экваториальный радиус) равна 6378245 м, а малая полуось (полярный радиус) - 6356863 м. Разность радиусов составляет 21 382 м. Для приближенных расчетов Землю принимают за равновеликую земному сфероиду сферу радиусом 6371 км.