Вокруг сжатой Земли

Сжатие вызывает наиболее сильное отличие фактической формы Земли от сферы, а ее гравитационного поля от центрального. Возмущающее влияние сжатия на движение спутников Земли сказывается значительно сильнее, чем суммарное влияние всех гармоник фигуры Земли и даже сопротивление атмосферы. Например, если спутник совершает полет по экваториальной орбите на высоте 230 км, то его возмущающее ускорение от сжатия Земли, направленное вдоль орбиты, составит 1,4 см/сек² и меньше основного ускорения, обусловленного притяжением Земли (914 см/сек²), в 656 раз. В направлении радиуса орбиты возмущающее ускорение будет в два раза большим. В то же время возмущающее торможение атмосферы на такой высоте полета для спутника массой 100 кг с поперечным сечением 1 м² составляет лишь 1/50000 долю от основного ускорения.

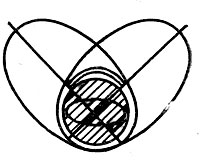
Рис. 28. Поворот орбиты в ее плоскости за счет сжатия Земли

С повышением высоты полета влияние сжатия будет уменьшаться. В точных расчетах его влияние проявляется даже на расстояниях, достигающих орбиты полета Луны. Траектория движения Луны как естественного спутника Земли всегда определяется с учетом сжатия Земли.

Несферичность Земли вызывает периодические и вековые изменения элементов орбит спутников Земли. Эти изменения в сильной степени зависят от положения плоскости орбиты в пространстве, в частности, от ее наклонения.

Наиболее ощутимые изменения - вековые, которые непрерывно и неумолимо возрастают от витка к витку. Они выражаются в том, что, во-первых, орбита начинает вращаться в своей плоскости (так называемое вековое перемещение точки перигея орбиты). Здесь сжатие выступает в роли своеобразного механизма, автоматически поворачивающего ось орбиты вокруг центра Земли (рис. 28). Максимальный угол поворота перигея для гипотетических спутников, совершающих полет непосредственно у поверхности Земли, составляет за один виток 0,3 градуса. Для спутников, двигающихся в районе орбиты Луны, этот угол уменьшается до 0,3 угл. сек. за виток. Угловая скорость поворота перигея зависит от наклонения орбиты и достигает наибольшей величины при наклонениях 45° и 135°, Для полярных (i = 90°) и экваториальных (i = 0°) эффект поворота орбиты в ее плоскости исчезает.

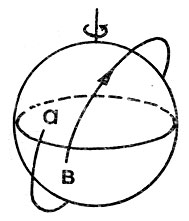
Рис. 29. Прецессия узла орбиты за счет сжатия Земли. Дуга ab показывает смещение узла за один виток

Во-вторых, сжатие Земли приводит к вращению плоскости орбиты в пространстве вокруг оси, совпадающей с осью Земли (так называемое вековое смещение узла орбиты). В результате узел орбиты от витка к витку постоянно смещается в направлении с востока па запад (рис. 29). Для спутников, движущихся в непосредственной близости от поверхности Земли, максимальное смещение узла за виток равно 0,6 градуса. Это означает, что через каждый виток трасса спутника будет проходить западнее на 33,5 км. На расстояниях до Луны эти смещения уменьшаются до 0,6 угл. сек и 0,5 км соответственно. Наибольший вековой уход узла наблюдается у орбит, плоскости которых приближаются к экватору (i = 0°). Для полярных орбит вековой уход узла исчезает, и плоскость орбиты будет сохранять неизменное положение в пространстве.

Таким образом, переменность силы тяжести, вызванная сжатием Земли, вызывает весьма существенное вековое смещение орбит искусственных спутников. Когда орбита спутника определена, что она может рассказать о форме Земли? Оказывается, маленький спутник является как бы носителем бесценной информации о форме Земли. Пробегая многомиллионный путь вокруг Земли, он оставляет невидимый след, в котором в зашифрованном виде записана вся поднаготная Земли, скрытая от взоров людей. Задача баллистиков - расшифровать эту тайнопись. Вот как это можно сделать. За сутки плоскость орбиты повернется вокруг оси Земли на заметный угол. Например, для третьего советского искусственного спутника Земли перемещение долготы узла составляло 2,6 градуса за сутки. Значит, примерно через 140 суток плоскость орбиты, совершив полный оборот, вернется к исходному положению. Положение плоскости орбиты по непосредственному наблюдению за движеним спутника относительно звезд определяется с высокой точностью, составляющей сотые доли градуса. Иначе говоря, средняя скорость вращения плоскости орбиты может быть определена с относительной ошибкой порядка одной десятитысячной. В свою очередь теоретические исследования показывают, что скорость поворота плоскости орбиты пропорциональна сжатию Земли. Следовательно, если не учитывать иные сопутствующие явления, непосредственно по наблюдению за спутниками можно получить данные по сжатию Земли с ошибкой в пределах одной тысячной.

Не прошло и года после запуска первых спутников, как были измерены скорости поворота плоскостей их орбит и найдено новое значение для сжатия. По данным английского ученого Десмонда Кинг-Хилли, оно заключается между 1/298,2 и 1/298,3 и существенно отличается от предшествующей величины 1/297,1. Маленький спутник Земли, это замечательное творение человеческих рук, позволил приподнять еще одно покрывало над таинственной фигурой Земли. По старой оценке сжатия экваториальный диаметр Земли больше полярного на 42,94 км, а по новой - на 42,77 км. Спутник как бы снял с полюсов слой воды, льда и грунта толщиной 85 м.

В-третьих, сжатие Земли вызывает вековое смещение спутника вдоль орбиты, что приводит к изменению периода его обращения по сравнению с периодом обращения вокруг сферической Земли. Для низколетящих спутников такое отличие достигает 0,35 мин за виток, или 167 км вдоль орбиты. Для спутников, летающих в районе орбиты Луны, получаем вековое возмущение периода 0,045 мин и смещение вдоль орбиты - 2,8 км за один виток (один месяц). На эту же величину смещается Луна после каждого оборота вокруг Земли.

Таковы, в основных чертах, вековые возмущения орбит спутников Земли, обусловленные ее сжатием. "Самопроизвольное" вращение перигея орбиты в ее плоскости и, в свою очередь, постоянное вращение плоскости орбиты вокруг оси Земли часто называют прецессией перигея и прецессией узла. Прецессия орбиты может существенным образом изменить положение орбиты в пространстве, поменять местами точки перигея и апогея. Она позволяет также без дополнительных энергетических затрат совместить плоскость орбиты космического аппарата с линией Солнце - Земля или любой другой линией, образующей постоянный угол с линией Солнце - Земля. В результате можно найти такую орбиту, чтобы она всегда одной стороной своей плоскости была постоянно обращена к Солнцу. Для этого необходимо выбрать такое наклонение орбиты (между 90° и 180°), при котором скорость прецессии узла сравнялась бы с видимой угловой скоростью движения Солнца относительно звезд.

Кроме вековых, сжатие вызывают и так называемые периодические возмущения орбиты, которые в среднем не изменяют орбиту спутника и ее положение в пространстве. Периодические возмущения как бы наслаиваются на основную невозмущенную орбиту, образуют на ней вмятины и вспучивания и, кроме того, несколько искореживают ее в пространстве. Эти отклонения не остаются стационарными вдоль орбиты и "плавают" вдоль нее по мере прецессирования орбиты. Наиболее сильные периодические возмущения возникают у низколетящих спутников и могут достигать 21 км вдоль орбиты и по направлению радиуса и 5 км - по нормали к плоскости орбиты.

Таким образом, несферичность Земли вызывает не только большие вековые, .но и значительные .периодические возмущения орбит спутников. По мере удаления от Земли значения возмущений убывают обратно пропорционально расстоянию до Земли, Луны.

Сжатие, если угодно, не проходит бесследно для Земли. Мы имеем в виду не ее фигуру, а движение по орбите вокруг Солнца, а также направление оси своего вращения.

Если бы Земля была однородным телом, то она притягивалась бы к Солнцу и Луне как материальная точка и ничто не заставило бы ее изменить направление оси собственного вращения в пространстве. Но, как нам известно, Земля представляется сложным телом, имеющим заметное утолщение на экваторе. Поэтому сила притяжения Солнца действует на более близкую к нему часть экваториального утолщения сильнее, чем на более далекую. Большую часть года Солнце отстоит далеко от плоскости экватора Земли, в результате образуется момент сил, который стремится развернуть Землю так, чтобы плоскость ее экватора совпала с направлением на Солнце.

Луна, находясь на значительно меньшем расстоянии от Земли, производит аналогичным образом еще более сильное влияние, стремясь также совместить плоскость экватора с плоскостью своей орбиты. В результате совместного действия этих сил плоскость экватора действительно стремится совместиться с плоскостью эклиптики. Но этому противодействует вращение. Земли вокруг своей оси. Земля уподобляется вращающемуся волчку, на который действует некоторый опрокидывающий момент сил. Под действием момента сил волчок, как известно, не, падает, а только отклоняет ось вращения в направлении, перпендикулярном линии действия возмущающей силы. По этой причине ось вращения Земли начинает сложным образом колебаться в пространстве. За счет влияния Солнца конец оси описывает на небесной сфере конус с углом раствора у вершины около 47° и периодом примерно 26000 лет. Одновременно совокупное влияние Солнца и Луны вызывает небольшие периодические колебания оси Земли с периодом 18,6 года. Конечно, эти колебания Земли мы совершенно не ощущаем и они ничем не проявляются на жизненных циклах Земли. Однако они доставляют много хлопот астрономам и баллистикам. Астрономы измеряют положения небесных светил относительно местного горизонта Земли в той ее точке, где расположен измерительный инструмент, а затем уже для единообразия пересчитывают их координаты относительно экватора Земли. Но с поворотом оси Земли одновременно поворачивается и экватор, причем это вращение идет непрерывно по очень сложному закону. В результате найденные с большим трудом координаты светил изменяются. Для отыскания их новых значений возникает необходимость ввести специальные поправки, которые обнаруживаются путем непосредственных измерений высот заранее выбранных небесных светил. Этой "неблагодарной" работой занимается специально созданная международная служба широты, широко разветвленная по всему земному шару. И когда космический аппарат совершил плавный спуск в атмосфере Венеры, то следует иметь в виду, что этому успеху содействовали и те, кто занимается определением направления оси вращения Земли.

Вот во что выливается совсем незаметное для нас сжатие нашей прекрасной Земли.

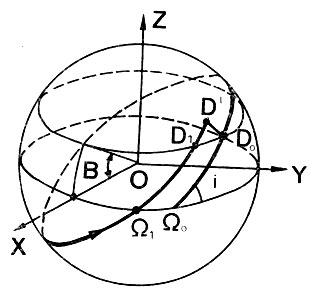
Рис. 30. Связь между различными периодами обращения

Вопрос, на первый взгляд, звучит странно. По первому впечатлению период обращения - это время совершения одного витка вокруг Земли. Говоря так, мы молчаливо предполагаем, что начало витка, т. е. начало траектории движения космического аппарата, и его конец, т. е. конец траектории, проходят через одну и ту же точку пространства. Именно такое условие соблюдается при движении в центральном поле сил. От витка к витку аппарат пробегает одну и ту же орбиту и два любые витка, как близнецы, схожи между собой. Здесь период обращения определен четко и однозначно. А что делать, если начало и конец витка не совпадают, но лежат где-то недалеко друг от друга? Например, за счет влияния сжатия спустя виток конец его оказывается сдвинутым по долготе на расстояние в несколько десятков километров. С течением времени этот сдвиг траектории увеличится и конец ее может оказаться на противоположной стороне Земли от начала траектории. В этих случаях теряется однозначность отсчета периода обращения, присущая эллиптической теории. Продолжительность витка каждый может отсчитывать по-своему, исходя из тех или иных геометрических либо физических соображений. Вот поэтому в астрономии и космической баллистике появились разные признаки определения начала и конца витка. В общем случае период обращения определяют как промежуток времени между двумя последовательными прохождениями центром спутника некоторой заданной поверхности. В качестве такой поверхности обычно берут плоскость экватора Земли, конус постоянной геоцентрической широты с вершиной в центре Земли, плоскости большого круга, проведенные через центры Земли под тем или иным углом к плоскости орбиты и др. В зависимости от выбора поверхности будет меняться и величина периода обращения. Наиболее употребительными на практике являются следующие периоды обращения искусственных спутников Земли:

Драконический период обращения - промежуток времени между двумя последовательными прохождениями спутника через плоскость экватора при движении с юга на север. Иначе говоря, он соответствует времени между двумя прохождениями спутника через восходящие узлы Ω₁ и Ω₂ двух последовательных витков орбиты (рис. 30). Если спутник выведен на эллиптическую орбиту, то при полете в гравитационном поле сжатой Земли его драконический период будет беспрерывно изменяться по некоторому сложному периодическому закону, не выходя при этом за некоторые границы. Это происходит в результате вращения орбиты в ее плоскости. Перигей будет постепенно обегать все положения вокруг Земли и спутник от витка к витку будет с разными скоростями проходить части орбиты, лежащие к северу от экватора и к югу от него. В результате время пребывания его в каждом из полушарий будет также изменяться, что и приводит к колебанию величины периода обращения.

Период обращения, соответствующий некоторой геоцентрической широте (он не имеет собственного имени), - промежуток времени между двумя последовательными прохождениями спутника через точки D₀ и D₁), лежащие на конической поверхности постоянной геоцентрической широты В, при движении его с юга на север.

Сидерический период обращения - время полета от некоторой точки D₀ орбиты до точки D₁, которая лежит в плоскости, проходящей через радиус-вектор OD0 перпендикулярно плоскости орбиты в точке D₀.

Последние два периода обращения в силу указанных причин также не будут постоянными.

Существуют и иные определения периодов обращения, уже не связанные с пересечением спутником тех или иных поверхностей.

Аномалистический период обращения - время между двумя последовательными прохождениями спутника через собственный перигей орбиты. Как бы ни были разнообразны возмущающие силы, как бы ни деформировалась под их влиянием орбита, на протяжении некоторого времени полета на ней всегда можно обнаружить последовательные точки, наименее удаленные от центра Земли. Вот их и принято называть перигеями. Конечно, это несколько не то, что наблюдается в эллиптическом движении, но в какой-то мере отражает "эллиптичность" орбиты. Однако определение аномалистического периода становится затруднительным или даже невозможным, когда орбита движения близка к круговой, для которой положение перигея становится неопределенным.

Особое место занимает так называемый оскулирующий период обращения. Чтобы понять физический смысл этого периода, предположим, что в некоторый момент времени нам известны все шесть кинематических параметров движения спутника, т. е. три его координаты и три составляющих вектора скорости. Независимо от того, действуют ли в последующем движении возмущающие силы или же полет происходит в центральном поле сил, оба эти движения - возмущенное и невозмущенное - начинаются с одной и той же точки с одинаковой начальной скоростью. По этим координатам и скорости можно определить все эллиптические элементы орбиты, т. е. высоты перигея, апогея, эксцентриситет, положение плоскости орбиты в пространстве, самой орбиты в этой плоскости и, конечно, период обращения, причем найденные элементы отнесены к заданному моменту времени. Если бы возмущающие ускорения отсутствовали, то в последующем движении в любой момент времени значения этих элементов, в том числе и периода обращения, сохранились. Вычисленные на некоторый момент времени по данным координатам и скорости, полученным на реальной орбите, эллиптические элементы орбиты называются опекулирующими. Значит, оскулирующий период представляет собой период обращения невозмущенной орбиты, по которой бы стал двигаться спутник, если бы, начиная с данного момента времени, исчезли все возмущающие ускорения.

Роль оскулирующих элементов в решении различных задач динамики движения космических аппаратов чрезвычайно велика. Формально они позволяют свести возмущенное движение к непрерывно меняющемуся кеплеровому движению. Вот как это объясняет Г. Н. Дубошин на страницах своей книги "Небесная механика".

"Представим себе: что в начальный момент времени на точку, движущуюся под действием силы притяжения центральной массы, подействовала дополнительная мгновенная возмущающая сила, величина которой весьма мала по сравнению с главной силой притяжения. Эффект этой мгновенной силы скажется тогда только на изменении начальных условий, так что начальные координаты и составляющие скорости получат в начальный момент весьма малые приращения (начальные возмущения!). Тогда "возмущенное движение" будет, очевидно, совпадать с некоторым кеплеровским движением, отличающимся от невозмущенного движения только начальными условиями. Поэтому последующие возмущения координат и составляющих скорости будут обусловлены только изменением начальных условий... Разумеется, что и элементы кеплеровской орбиты такого возмущенного движения будут отличаться от элементов первоначального, ничем не возмущенного движения. Мы можем сказать также, что мгновенно действовавшая возмущающая сила сообщила элементам орбиты некоторые возмущения (начальные возмущения элементов)...

Представим теперь опять невозмущенное движение, определяемое заданными начальными условиями и протекающее под действием одной только силы притяжения центрального тела. Пусть в некоторый момент времени, отличный от начального, движущаяся материальная точка испытала действие малой возмущающей силы. Тогда эффект этой силы будет совершенно аналогичен эффекту действия мгновенной силы в начальный момент. Таким образом, в рассматриваемый момент времени координаты и составляющие скорости получат малые приращения (возмущения), а следовательно, изменятся также мгновенно и элементы орбиты. В дальнейшем движение точки опять будет происходить в полном согласии с законами Кеплера по кеплеровской орбите, но с возмущенными элементами.

Подобные рассуждения можно повторять для каждого момента времени. Следовательно, если мы вообразим бесконечный ряд моментов времени, отделенных друг от друга бесконечно малыми промежутками, и будем считать, что в каждый из этих моментов действует мгновенная возмущающая сила (равная нулю в промежутках между указанными моментами), то мы получим примерную схему возмущенного движения. Истинное или возмущенное движение точки можно будет рассматривать в этой схеме как некоторое кеплеровское движение, элементы которого изменяются скачкообразно в каждый из моментов действия мгновенной возмущающей силы. Притом ясно, что измененное (возмущенное) и неизменное (невозмущенное) в момент t движения исходят в этот момент из одной и той же точки пространства и их траектории имеют в этой точке общую касательную.

Увеличивая мысленно число таких моментов времени и одновременно уменьшая неограниченно промежутки между ними, мы придем в пределе к движению, которое можно рассматривать, как непрерывно изменяющееся кеплеровское движение с непрерывно изменяющимися элементами. Отсюда следует, что для определения такого (истинного или возмущенного) движения мы можем пользоваться всеми формулами невозмущенного движения, рассматривая в последних все элементы орбиты (и величины, от них зависящие) как некоторые непрерывные функции времени, которые должны быть соответственным образом определены".

Подобный механизм описания возмущенного движения широко применяется на практике. Он позволил найти приближенные аналитические зависимости, позволяющие с любой степенью точности находить малые поправки к элементам невозмущенного движения и удобно учитывать воздействия различного рода дискретных и непрерывных возмущающих сил.

Теоретические исследования показали, что при движении спутников в реальном поле Земли ряд элементов орбит на относительно небольшом отрезке времени достаточно близки к оскулирующим (невозмущенным). Это позволяет в ряде случаев определить элементы орбит как сумму их оскулирующих значений и небольших поправок к ним. Однако это совсем не устраняет разницу в величинах различных периодов. Вот поэтому часто становится непонятной фраза: "Спутник выведен на орбиту с периодом обращения..." Вы можете разгадать эту загадку, т. е. определить, что это за период? Автор не берется.