Космонавт и ракетный двигатель

Итак, чтобы обезопасить выход в открытый космос и обеспечить возвращение на корабль, космонавту необходим ракетный двигатель. Ракетный двигатель преобразует энергию топлива в кинетическую энергию газового потока, истекающего с высокой скоростью из сопла, и тем самым создает тягу, направленную в сторону, противоположную вектору скорости истечения газа.

Действие тяги ракетного двигателя на движение космонавта обычно оценивается величиной создаваемого двигателем ускорения. При свободном движении в космосе даже малое по величине ускорение с течением времени может привести к значительному изменению скорости и длины пути космонавта. Чтобы оценить это, давайте предположим, что притяжение планет отсутствует и на космонавта действует единственная сила - это тяга двигателя.

В космической баллистике обычно рассматриваются два случая: движение космонавта при постоянном ускорении и движение под действием постоянной тяги.

Первый случай означает, что в процессе полета тяга двигателя регулируется так, что ускорение космонавта будет постоянным. При этом величина тяги двигателя с течением времени должна уменьшаться, так как уменьшается масса космонавта за счет истечения газов через сопло двигателя.

Расчеты показывают, что даже столь малое ускорение, равное всего 1 см/сек², за время завершения одного витка приведет к смещению космонавта на 145 км. Напомним, что такое смещение получается при отсутствии притяжения планет и постоянном направлении действия тяги двигателя.

Во втором случае, когда тяга двигателя остается постоянной (уместно указать, что этот случай наиболее просто реализуется на практике), расчет скорости полета космонавта без учета действия притяжения планет производится по знаменитой формуле К. Э. Циолковского:

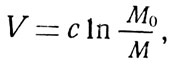
где V - скорость полета космонавта, с - скорость истечения газов, М₀ - начальная и М - конечная масса космонавта вместе с двигателем. Отношение масс М₀/М носит название числа Циолковского и обычно обозначается буквой z.

Наименьшее значение числа Циолковского равно 1 и ему соответствует момент времени включения двигателя. В процессе работы двигателя число Циолковского возрастает. Так, если к моменту выключения двигателя число z увеличится до 1,030, то скорость космонавта составит 0,03 от скорости истечения газов. А это означает, что при скорости истечения 1 км/сек скорость космонавта увеличится на 30 м/сек.

Из формулы Циолковского следует, что чем выше скорость истечения газов, тем большую скорость получит космонавт при одном и том же расходе топлива. С повышением скорости истечения уменьшается также расход газа для создания одной и той же тяги.

Таким образом, при нахождении в открытом космосе воздействие даже относительно малых тяг (сил) с течением времени может привести к существенному изменению характера движения космонавта. Не случайно, что в ряде случаев при длительных полетах космических аппаратов (в частности, при полетах к Марсу, Венере) учитывается воздействие столь ничтожной силы, как давление солнечного света (она составляет величину менее одного миллиграмма).

Этого эффекта мы совершенно не наблюдаем при движении по поверхности Земли. Например, сила 0,1 кг не в состоянии даже стронуть с места велосипедиста, тогда как в космосе спустя первые 100 сек после начала действия такой же силы велосипедист имел бы скорость около 1 м/сек. В этом состоит одно из существенных отличий эффекта воздействия тяги на движение в космосе и по Земле.

Другое отличие заключается в способе приложения тяги. Исходя из формулы Циолковского, скорость, которую приобретает космонавт, не зависит от времени работы двигателя, а только лишь от отношения масс и скорости истечения газов. Другими словами, полученная скорость будет одной и той же, если топливо сжигать мгновенно, отдельными порциями, или же непрерывно, но медленно. В первом случае баллистики говорят, что тяга двигателя является импульсной, во втором - непрерывной.

Иначе обстоит дело при движении по Земле. Например, чтобы автомобиль двигался непрерывно, на него также непрерывно должна воздействовать тяга. Если же тяга приложена в виде импульса (автомобиль толкнули), то через некоторое время из-за влияния сил сопротивления он остановится. В этом смысле космический пешеход находится в гораздо лучших условиях: один раз оттолкнувшись, он уже никогда сам по себе не прекратит своего движения.

Итак, космонавт, вооруженный двигателем и мечтающий совершить приятную и безопасную прогулку, вышел в открытый космос, включил двигатель и... Что с ним произошло после этого, вы узнаете, прочитав последующие страницы книги.