Космонавт совершает полет совсем не в ту сторону, куда направлена тяга двигателя

Чтобы показать особенности и сложности свободного движения космонавта в открытом космосе при непрерывно работающем ракетном двигателе, рассмотрим ряд интересных случаев. Для определенности будем полагать, что к моменту включения двигателя космонавт вместе с кораблем двигался по круговой орбите спутника Земли с высотой 200 км. Двигатель развивает тягу 0,1 кг, т. е. при массе космонавта 100 кг его ускорение движения будет составлять примерно 1 см/сек².

Ранее мы убедились, что в случае отталкивания космонавта от корабля-спутника траектория его последующего движения относительно корабля, вопреки предположениям, оказывается достаточно сложной и зависит от направления отталкивания. Очевидно, что и при непрерывной работе двигателя следует также ожидать новых парадоксов движения, которые еще больше усложняют и без того тяжелые условия пребывания космического пешехода в космосе.

Итак, предположим, что космонавт вышел из корабля, включил двигатель и, пользуясь одним из описанных способов, развернулся так, что струя газов, вытекающих из сопла, была направлена к центру Земли, и в этом положении стал совершать полет. В этом случае тяга двигателя будет направлена от Земли вдоль радиуса орбиты и как бы отталкивать космонавта в спину от корабля (и от Земли) вверх. Если вы пожелаете дать качественный прогноз последующего движения, то он может выглядеть примерно так: поскольку тяга двигателя действует непрерывно и направлена все время вверх, то с течением времени космонавт все дальше и дальше будет удаляться от корабля, орбита его будет повышаться и он в конце концов покинет Землю. Но так ли это на самом деле? Ведь цепи земного тяготения порвать нелегко!

Мы уже познакомились с необычностью движения космического пешехода. Здесь она тоже наверняка присутствует и поэтому наш предварительный прогноз едва ли является правильным. Действительно, воздействие постоянной радиальной тяги двигателя можно истолковать как уменьшение притяжения Земли, т. е. словно бы в момент включения двигателя притяжение Земли скачком уменьшилось на величину, равную тяге двигателя. Тогда последующее движение космонавта можно формально рассматривать свободным (без тяги двигателя), oно в поле Земли с меньшей силой притяжения.

Однако здесь необходимо сделать одно замечание. В процессе движения на космонавта действуют три следующие основные силы: сила притяжения Земли, центробежная сила и сила тяги двигателя, причем две последние силы действуют в одном направлении. Величина силы притяжения определяется по закону Ньютона и зависит от радиуса орбиты: чем больше радиус, тем эта сила меньше, и наоборот. Если бы движение космонавта происходило на одной и той же высоте, то сила притяжения оставалась бы постоянной. Значит, разность этой силы и силы тяги двигателя тоже должна оставаться постоянной. И, чтобы описать движение космонавта, достаточно раз и навсегда уменьшить силу притяжения Земли на величину этой разности и в последующем считать гравитационное поле центральным и постоянным во времени. Однако в процессе работы двигателя высота полета может изменяться. Следовательно, будет изменяться также сила притяжения Земли, а также разность ее и силы тяги, поскольку тяга остается (по условию) постоянной. Отсюда следует, что для того, чтобы задачу расчета полета космонавта с работающим двигателем свести к задаче расчета полета без двигателя, необходимо силу притяжения Земли, т. е. ее массу, изменять по определенному заколу. Такая задача в принципе решается, однако здесь нет необходимости входить в тонкости точного расчета, а достаточна ограничиться его приближенной аналогией. В качестве допущения можно принять, что относительное изменение высоты орбиты является небольшим и поэтому изменением силы притяжения Земли можно пренебречь. Отсюда сразу следует вывод: движение космонавта происходит как бы в центральном поле сил с уменьшенной массой Земли и, следовательно, орбита его движения вокруг Земли будет замкнутой кривой. А это означает, что при воздействии радиальной тяги космонавт никогда не покинет Землю.

Необходимо оговориться, что полученный качественный вывод справедлив только для достаточно малых тяг. Если же тяга двигателя превышает некоторую строго определенную величину, то космонавт навсегда покинет Землю. Эта величина тяги определяется ускорением, создаваемым двигателем. Оно должно составлять более одной восьмой от ускорения силы тяжести на данной высоте полета. В рассматриваемом нами случае тяга двигателя должна составлять примерно 12 кг.

Определим теперь приближенную форму орбиты. До включения двигателя орбита космонавта была круговой и, следовательно, в момент включения двигателя вектор скорости его полета был направлен параллельно горизонту. Значит, в этой точке будет расположен апогей или перигей орбиты. Но так как скорость полета в этой точке для начальной массы планеты была круговой, то для уменьшенной массы планеты она станет выше круговой. А эта точка, как известно, является перигеем орбиты.

Таким образом, мы приходим к следующему выводу: при радиальном воздействии тяги орбита космонавта в первом приближении описывается замкнутой кривой, целиком охватывающей круговую орбиту. Период обращения космонавта увеличивается и поэтому в процессе полета он будет отставать от корабля-спутника. Схематически это изображено на рис. 56, а. В точке О производится включение двигателя, а точками 1 - 1′, 2 - 2′ и т. д. обозначены соответствующие положения корабля и космонавта в одни и те же моменты времени на первом витке полета.

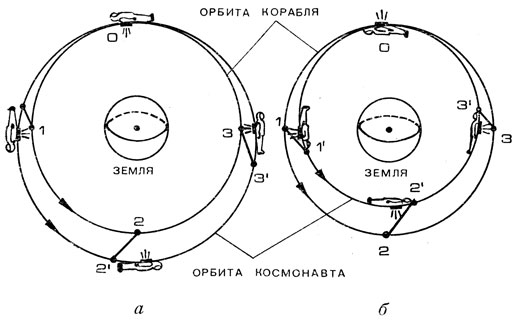
Рис. 56. Орбиты космонавта и корабля: а - тяга направлена от центра Земли; б - тяга направлена к центру Земли

Как видим, результат воздействия постоянной радиальной тяги чем-то напоминает случай отталкивания космонавта от корабля в направлении скорости его полета, который был уже рассмотрен в предыдущей главе.

Строгий математический анализ показывает, что в действительности орбита космонавта не является эллипсом, а лишь в какой-то мере приближается к нему. Для радиальных тяг двигателя, соответствующих выполнению условия "меньше 1/8", но близких к этой величине, движение космонавта будет происходить в плоскости орбиты корабля, а орбита его не выйдет за круг, радиус которого равен удвоенному радиусу начальной круговой орбиты.

Пусть теперь после отделения от корабля космонавт сориентировался так, что тяга двигателя направлена к центру Земли (космонавт обращен лицом к Земле). В этом случае аналогичным образом можно показать, что орбита его в первом приближении также будет являться замкнутой, но целиком лежать внутри круговой орбиты корабля (рис. 56, б). В точке включения двигателя будет расположен апогей. В процессе движения космонавт будет обгонять корабль, все время находясь ниже его, и только через каждый виток выходить на равную с кораблем высоту.

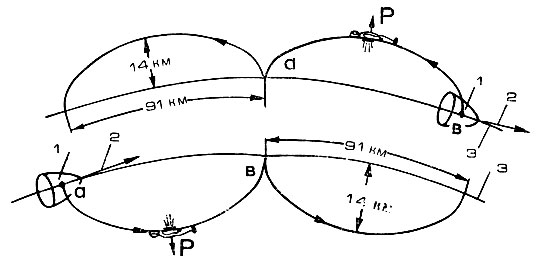
Рис. 57. Траектория движения космонавта относительно корабля при направлении тяги двигателя вверх и вниз: 1- корабль; 2 - скорость корабля относительно Земли; 3 - орбита корабля; aq - расстояние, на которое удаляется космонавт от корабля за один виток

Определив характер орбитального движения космонавта, теперь можно легко представить траекторию движения космонавта относительно корабля. Такие траектории показаны на рис. 57. Если тяга двигателя направлена от Земли (рис. 57), то траекторию движения, по аналогии с нашими "земными" представлениями, можно изобразить следующим образом: космонавт как бы становится на орбиту (головой вверх) лицом в сторону движения корабля и затем "подпрыгивает", отталкиваясь от орбиты вверх ,и назад. После такого "прыжка" космонавт будет подниматься вначале вверх и одновременно отставать от корабля. Спустя половину периода обращения (в нашем случае через 45 минут) он поднимется на наибольшую высоту, равную 14 км) а затем, ровно через виток после начала прыжка (т. е. спустя 90 минут), "опустится" "а начальную орбиту позади корабля на расстоянии 91 км. Такой высоте "прыжка" мог позавидовать даже Валерий Брумель.

Если же тяга двигателя направлена к центру Земли (рис. 57), то космонавт "становится" на орбиту спиной к направлению движения и "подпрыгивает" к Земле и вперед. В этом случае он уже обгоняет корабль.

С изменением величины тяги пропорционально увеличиваются или уменьшаются высота и дальность "прыжка". Так, если тяга двигателя уменьшится до 10 г (против 100 г), то высота станет равной 1,4 км и удаление за один виток - 9,1 км. Из этих примеров отчетливо видно, что даже небольшие силы, действующие непрерывно на космонавта, могут привести к существенному изменению его положения относительно корабля. В этом смысле космический пешеход действительно находится в значительно лучших условиях, чем пешеход на Земле.

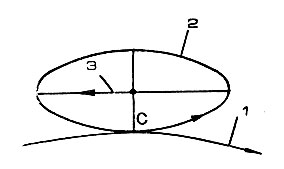
Рис. 58. Геометрическая интерпретация траектории относительного движения космонавта: 1 - орбита корабля-спутника; 2 - эллипс; 3 - скорость смещения эллипса

Траектории движения космонавта можно дать простую геометрическую интерпретацию. Это движение по эллипсу, касающемуся орбиты корабля, центр которого смещается вдоль орбиты с постоянной скоростью (рис. 58). В рассматриваемом случае полуоси эллипса равны: малая - 7 км, большая - 45,5 км. Скорость смещения (дрейф) центра эллипса составляет 17 м/сек. Если тяга действует вверх, то эллипс целиком расположен снаружи орбиты и "скользит" по орбите в сторону, противоположную полету корабля-спутника. Точка С соответствует моменту отделения космонавта от корабля и включения двигателя.

Таким образом, мы познакомились еще с одной "необычностью" движения космического .пешехода. Парадоксальность его движения состоит в том, что в процессе работы двигателя суммарное смещение 'космонавта от витка к витку происходит в сторону, перпендикулярную направлению действия тяги. С течением времени космонавт все дальше и дальше будет уходить от корабля, но через каждый виток возвращаться на начальную высоту.

Космонавт движется в направлении, противоположном действию тяги

Теперь рассмотрим второй случай движения космонавта при непрерывно работающем двигателе, когда тяга его направлена вдоль скорости полета корабля-спутника.

Мы уже неоднократно убеждались, что давать качественный прогноз движения космонавта относительно корабля не столь простое дело, как это может показаться с первого взгляда. Однако на этот раз мы будем довольно близки к истине, если скажем: в процессе работы двигателя космонавт все дальше и дальше будет удаляться от корабля.

Но... Это "но" сразу же настораживает: значит, и здесь все же имеются "аномалии" ожидаемого движения. Космический пешеход опять не желает подчиняться нашим привычным представлениям о движении. Давайте разберемся в этом.

Воздействие постоянной тяги на космонавта можно приближенно заменить непрерывно следующими друг за другом малыми по величине отдельными "толчками" (импульсами), направленными также вдоль скорости полета корабля. В результате воздействия первого из таких "толчков", как это было показано ранее, космонавт переходит на эллиптическую орбиту, охватывающую начальную круговую орбиту корабля. Второй "толчок", следующий за первым, еще больше увеличит размеры орбиты и т. д. В связи с переходом на более высокую орбиту. Скорость полета космонавта будет уменьшаться и поэтому он начнет отставать от корабля. Вот и обнаружился новый парадокс движения, оправдав тем самым сказанное ранее "но": воздействие непрерывной тяги, направленной вдоль скорости полета корабля, приводит в конечном счете к уменьшению скорости полета космонавта по орбите. Действительно, странный эффект - вместо разгона космонавт, независимо от своего желания, тормозится.

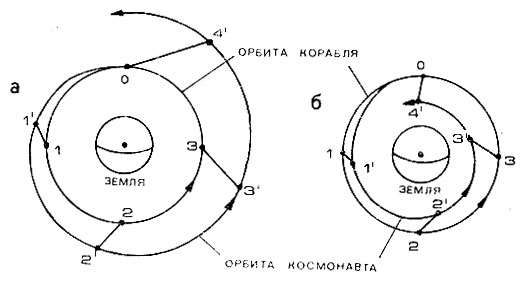
Рис. 59. Орбиты движения космонавта и корабля: а - тяга направлена вдоль скорости полета; б - тяга направлена навстречу скорости полета

Выявленный, на первый взгляд парадоксальный, характер движения объясняется тем, что в результате воздействия тяги двигателя механическая энергия космонавта возрастает. При этом возрастание ее в соответствии с законами небесной механики приводит к увеличению высоты полета и уменьшению скорости движения. Образно говоря, двигатель уподобляется своеобразному "насосу", который, с одной стороны, увеличивает механическую энергию и, с другой, "перекачивает" часть кинетической энергии (энергии движения) в потенциальную (энергию поднятого тела). Вот и второй пародокс: несмотря на то, что тяга двигателя всегда направлена параллельно горизонту, высота полета непрерывно возрастает, хотя в этом направлении тяга не действует. Суммарное изменение высоты и скорости полета приводит к тому, что космонавт будет двигаться вокруг Земли по разворачивающейся спирали с некоторыми периодическими колебаниями относительно спирального движения (рис. 59, а).

Если же тяга двигателя направлена навстречу скорости полета корабля, то будем наблюдать обратную картину: космонавт станет двигаться по сворачивающейся спирали, высота полета будет непрерывно уменьшаться, скорость станет возрастать и он обгонит корабль (рис. 59, б).

Траектория движения космонавта относительно корабля при действии тяги вдоль скорости полета показана на рис. 60, а.

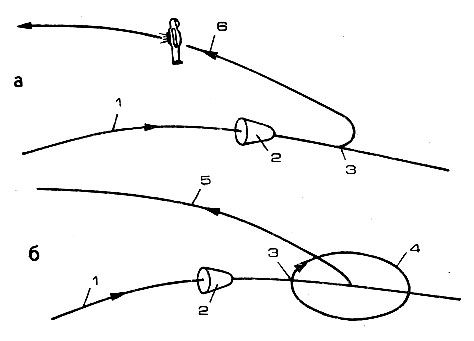
Рис. 60. Траектория движения космонавта относительно корабля при действии тяги в направлении скорости корабля: 1 - орбита корабля; 2 - корабль; 3 - точка включения двигателя; 4 - эллипс относительного движения; 5 - траектория движения центра эллипса; 6 - траектория движения космонавта

В начальный момент космонавт несколько обгоняет корабль, но уже спустя 26 мин после включения двигателя движение вперед прекращается и начиная отсюда космонавт будет двигаться навстречу скорости полета корабля. При указанных выше данных за время завершения одного витка космонавт отстанет от корабля на 430 км и поднимется на высоту 91 км.

Результат, прямо сказать, впечатляющий! Такой "прыти" от космического пешехода трудно было ожидать.

Траекторию движения космонавта приближенно можно интерпретировать так же, как движение по эллипсу, центр которого скользит по параболе (рис. 60). В процессе передвижения эллипса большая ось его остается параллельной горизонту. Полный оборот по эллипсу завершается за один виток и за счет этого возникает упомянутая ранее периодическая составляющая, наложенная на основное движение. Ось параболы касается орбиты корабля. В начальный момент центр эллипса лежит на орбите корабля впереди его на расстоянии 29 км, а затем смещается вверх со скоростью 17 м/сек и навстречу кораблю с постоянно увеличивающейся от нуля скоростью. Спустя виток скорость дрейфа эллипса, направленная навстречу скорости полета корабля, увеличится до 162 м/сек и от витка к витку будет возрастать на эту величину, т. е. на эту величину на каждом витке будет уменьшаться скорость движения космонавта на орбите. Центр эллипса спустя виток поднимется на высоту 91 км и отстанет от корабля примерно на 430 км.

Таким образом, движение космонавта относительно Земли по разворачивающейся спирали можно представить как сумму движений по параболе, вершина которой жестко связана с определенной точкой орбиты, находящейся впереди корабля, и эллипсу, центр которого скользит по параболе.

Аналогичным образом можно представить движение космонавта относительно корабля, если тяга двигателя будет направлена навстречу скорости полета. В этом случае вершина параболы будет лежать позади корабля, а ветвь ее, по которой скользит центр эллипса, направлена в сторону Земли к кораблю. Космонавт будет двигаться по эллипсу в противоположном направлении. Если величину тяги двигателя изменить, то пропорционально изменятся и характеристики движения (расстояния и скорости).

Любопытно отметить еще один интересный эффект. Выше было показано, что при движении космонавта вне поля притяжения планет за время, равное продолжительности одного витка (примерно полтора часа), под действием постоянной тяги величиной 0,1 кг он пройдет путь, составляющий 145 км. Если же космонавт движется в поле притяжения Земли (случай, рассматриваемый здесь), то при той же тяге и за то же самое время полета он сдвинется относительно корабля, как начальной точки отсчета, на значительно большее расстояние, равное 430 км. Этот, казалось бы, странный эффект влияния гравитационного поля объясняется указанным выше перераспределением кинетической и потенциальной энергий космонавта.