Внимание! Вы падаете на потолок!

С такими словами обратился к читателям Б. Коган на страницах журнала "Наука и жизнь" № 7 за 1969 г., когда рассматривал вопрос о движении внутри корабля, вращающегося с постоянной угловой скоростью с целью создания искусственной тяжести.

Мы уже упоминали, что создать искусственную силу тяжести можно посредством вращения космического корабля вокруг его оси. Все предметы, находящиеся в этом корабле, окажутся под действием центробежной силы, прижимающей их к полу. Подбирая нужную скорость вращения, можно добиться, что центробежная сила будет иметь такую же величину, как и привычная в земных условиях сила тяжести.

Но вот вопрос, который наверняка заинтересует будущих астрономов: как будет выглядеть траектория падающего внутри корабля тела? Например, астронавт выронил из рук шарик - где он упадет, у ног или где-либо в ином месте. Не может ли этот шарик ударить космонавта по голове? Вот на эти вопросы по существу и отвечает Б. Коган. Ход его рассуждений выглядит так.

Способ создания искусственной силы тяжести с помощью центробежных сил хорошо известен. Он не раз описывался в научно-фантастической литературе и на первый взгляд позволяет хорошо имитировать естественную земную тяжесть. Однако это верно лишь до тех пор, пока тела, находящиеся в космическом корабле, неподвижны. Если же они начнут двигаться, то окажутся под действием еще одной "искусственной" силы, порожденной вращением корабля, так называемой силы Кориолиса. Эта сила пропорциональна относительной скорости движущегося тела и направлена перпендикулярно вектору этой скорости. Поэтому сила Кориолиса может заметно изменить траекторию тела, движущегося в космическом корабле. Изменение это настолько велико, что вместо падения на пол может получиться падение на стену или даже на потолок.

Пусть, например, шар падает из точки Л внутри космического корабля (рис. 68, а). Если бы на этот шар действовала только центробежная сила, то он двигался бы по "вертикали" АВ и упал на пол в точке В. Однако на шар действует еще и сила Кориолиса FK. Двигаясь "вниз", шар одновременно смещается вбок и закончит свое движение не в точке В, а в точке В₁.

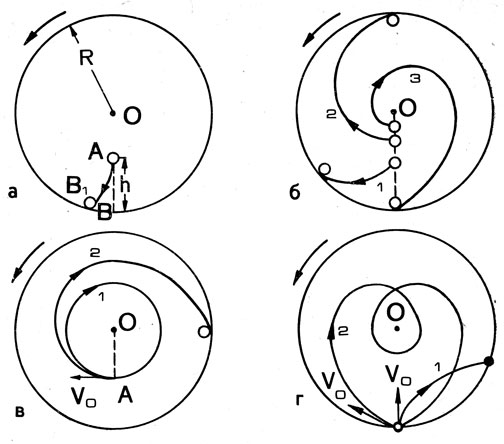
Рис. 68. Траектория падения тел внутри вращающегося корабля

Как велико расстояние BB₁? Расчет показывает, что оно зависит от высоты h и радиуса r. При этом, если r не слишком велик, то это расстояние оказывается весьма заметным. Например, если r равно 10 м и h = 1 м, то ВВ₁ будет равно 33 см, т. е. составит треть от высоты h. Если же увеличить h до 2 м, то расстояние ВВ₁ станет равным 106 см и превысит половину высоты падения. Эти цифры показывают, что сила Кориолиса может существенно исказить траекторию тела, падающего в космическом корабле.

Конечно, у вас сразу возникнет вопрос: а что это за таинственная сила Кориолиса, откуда она берется, когда ее необходимо учитывать и где можно наблюдать ее проявление в природе? Понять причину возникновения этой силы можно на рассматриваемом примере падения шарика в космическом корабле. Пусть до начала падения шарик находился в руке у космонавта, т. е. на расстоянии r от центра корабля. В то же время ноги космонавта будут опираться о пол в окрестности точки В. Следовательно, вращаясь вместе с кораблем, ноги космонавта будут иметь большую скорость движения, чем шарик, поскольку они расположены дальше от центра корабля. Когда шарик начинает падать "вниз", то скорость его, соответствующая скорости точки А, будет меньше скорости точки В. Значит, за время -падения точка В вместе с вращающимся корпусом корабля переместится на большее расстояние от исходного положения, чем падающий шарик. Вот по этой причине и возникло отклонение шарика на расстояние ВВ₁ от вертикали. Космонавт, обнаруживший это отклонение, может формально считать, что причиной отклонения послужила некая фиктивная, или "искусственная" сила, направленная по перпендикуляру - высоте АВ. Эту силу в механике и называют силой Кориолиса.

Сила Кориолиса проявляется также при движении по поверхности земного шара, обладающего определенной угловой скоростью благодаря суточному вращению. Пусть, например, вдоль меридиана проходит поезд в направлении на север в северном полушарии. Значит, по мере перемещения на север он переходит из областей больших линейных скоростей вращения Земли в меньшие. Уравнивание этих скоростей производится силой Кориолиса, направленной касательно земной поверхности, т. е. поезд оказывает на правый рельс большее давление, чем на левый. Существованием силы Кориолиса объясняется размывание реками в северном полушарии правого, а в южном - левого берегов, возникновение северо-восточных пассатов в северном полушарии и т. д. Но Земля вращается с ничтожной угловой скоростью по сравнению с кораблем и поэтому эти эффекты выражены слабо. Например, тело, находящееся на широте Москвы и падающее с высоты 50 м, отклоняется от вертикали на запад всего на 3 миллиметра.

Но вернемся к повествованию Б. Когана.

При дальнейшем увеличении h отклонение ВВ₁ быстро возрастает, а траектория падающего шара сильно искривляется (рис. 68,б). Например, при r = 10 м и h = 6 м траектория шара будет изображаться кривой 1, а отклонение от "вертикали" достигнет 11,3 м (если измерять его вдоль криволинейного пола корабля). Если же увеличить h до 7,8 м, то шар будет двигаться по кривой 2 и придет в точку, лежащую над тем местом, откуда он начал двигаться. Можно сказать, что этот шар падает не на пол, а на потолок. Наконец, если падение шара начнется с высоты 8,7 м, то он будет двигаться по траектории 3, которая, хотя и приводит его на иол, делает это весьма своеобразным способом.

Кривые, показанные на рис. 68, б, изображают траектории тела, начинающего падать из состояния покоя. Если же сообщить этому телу начальную скорость, то его траектория станет несколько иной. Пусть, например, шару, начинающему движение из точки А, сообщена относительная скорость 170, направленная так, как показано на рис. 68, в. Тогда характер его траектории будет зависеть от величины этой скорости, причем наиболее интересен тот случай, когда V₀ = ω х OA ( - угловая скорость вращения корабля). В этом случае шар будет двигаться по окружности 1, т. е. вообще не упадет на пол ("лишится" своего искусственного веса). Если же скорость V0 будет немного больше или немного меньше, то шар станет двигаться по спиральной траектории 2, постепенно приближаясь к полу.

Необычные траектории будут возникать и при других направлениях начальной скорости (если эта скорость не слишком велика). Две таких траектории показаны на рис. 68, г, первая из них получается, когда начальная скорость направлена "вверх", а вторая - когда она направлена "под углом" (и имеет подходящую величину). Траектория 2 очень далека от тех, какие мы привыкли видеть в земных условиях.

Все эти странные траектории представляются такими лишь наблюдателю, находящемуся внутри корабля. Если же глядеть на них "со стороны", т. е. находясь в системе координат, участвующей только в поступательном движении корабля, то они будут казаться прямолинейными. Действительно, так как в этой системе нет ни центробежной силы, ни силы Кориолиса, то тело, предоставленное самому себе, движется здесь по инерции - прямолинейно и равномерно. В частности, оно может быть в этой системе неподвижным, и тогда наблюдателю, находящемуся во вращающемся корабле, будет казаться, что оно движется по окружности. Именно в этом случае получается траектория 1, показанная на рис. 68, г.

Таким образом, во вращающемся космическом корабле сила Кориолиса проявляется достаточно сильно. Только что описанные траектории падения шарика (будут одинаковыми независимо от угловой скорости вращения корабля, ибо одновременно с ее изменением будет также изменяться и центробежная сила, и время падения шарика.

Любопытно, наконец, отметить, что если космонавт, стоя на полу космического корабля лицом в направлении его вращения, будет наклоняться, то сила Кориолиса начнет опрокидывать космонавта назад. Если же перед наклоном он стоял лицом в направлении оси вращения, то после наклона эта же сила будет стремиться повернуть его на полу. При относительно небольших размерах корабля и высокой угловой скорости его вращения силы Кориолиса могут достичь заметных величин и это потребует от обитателей космического корабля выработки определенных навыков в координации своих движений. Иначе очень просто оказаться .на полу.