Невесомость и деформации

Невесомость, силы инерции, деформации... Мы привыкли к этим понятиям и свободно оперируем ими, часто совершенно не отдавая отчета в строгости и 'правильности их употребления. Однако это далеко не простые вещи. Они рассматривались и раньше, но только с наступлением космической эры приобрели конкретный смысл. С вопросами о физической сущности состояния невесомости как одном из аспектов проблем космических полетов, силы инерции, силы тяготения и их эквивалентности можно подробно ознакомиться в книге С. Э. Хайкина "Силы инерции и невесомость", вышедшей из печати в 1967 г. в изд. "Наука". В книге дается достаточно глубокое, но и вместе с тем популярное, доступное неспециалисту объяснение рассматриваемых вопросов.

Акцентируя свое основное внимание на динамике движения космических аппаратов, мы не ставим перед собой задачу сколько-нибудь подробно изложить проблему невесомости, сил инерции и т. д., даже используя названную книгу, но воспользуемся ее некоторыми результатами. Вот что пишет С. Э. Хайкин о состоянии невесомости..

Вообще, при любой начальной деформации тела, вызванной силами тяготения, после того как началось свободное падение, деформации будут уменьшаться и постепенно исчезнут. Этот случай, когда тело движется под действием только силы тяготения и поэтому находится в недеформированном состоянии, является особым в том смысле, что он может наступить под действием только массовых сил, т. е. только сил тяготения. Так как тело находится в недеформированном состоянии, то в нем отсутствуют все упругие силы "и, в частности, силы веса. Такое состояние, когда на тело действуют только силы тяготения, но в теле не возникает силы веса, и называется состоянием невесомости.

Сила тяготения в состоянии невесомости действует, и при этом "во всю мочь", так как она сообщает телу, находящемуся в состоянии невесомости, именно то ускорение, которое она должна ему сообщать, - ускорение свободного падения. Вместе с тем, поскольку никакие другие силы на это тело извне не действуют, все его элементы испытывают одинаковое ускорение, деформации в теле не возникают, вследствие чего и силы веса отсутствуют.

Итак, в системе тел наступает состояние невесомости, если всем входящим в эту систему телам и всем частям этих тел одинаковые ускорения сообщают силы тяготения и также одинаковые ускорения сообщают силы инерции. В рассматриваемом нами случае, когда система координат связана с центром масс космического корабля, испытывающего ускорение под действием только сил тяготения, мы обычно можем ограничиться малой областью пространства, в которое заключены корабль и находящиеся вблизи него тела. В этом случае как силы тяготения, так и силы инерции сообщают всем телам одинаковые ускорения, причем те и другие ускорения оказываются равными по величине (но противоположными по направлению), в результате чего связанная с кораблем система координат оказывается инерциальной.

Однако, если размеры системы тел велики, возможны такие oслучаи, когда, хотя на тело отсчета, с которым связана система координат и все другие тела системы, действуют только силы тяготения и силы инерции, все же сумма этих сил не равна нулю. Рассмотрим один из таких принципиально возможных случаев. Вообразим, что на большую высоту над поверхностью Земли (которая для упрощения рассуждений не вращается) заброшена (при помощи ракеты) кабина, к днищу которой на очень длинном тросе прикреплен груз т (рис. 69) примерно такой же массы, как и масса кабины. Все это сооружение свободно падает под действием силы земного притяжения. Так как груз т находится ближе к центру Земли, чем кабина, то Земля будет сообщать кабине и -всем находящимся в ней телам меньшее ускорение, чем грузу. Ясно, что при этом трос натянется, вследствие чего ускорение кабины увеличится и окажется несколько больше, чем ускорение свободного падения тела, находящегося в кабине. Поэтому тело массы т, 69. свободно лежавшее на дне кабины, будет отставать в своем свободном падении на Землю от дна кабины, т.е. по отношению к кабине будет все время "подниматься к верху".

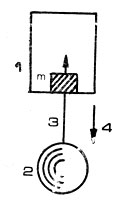
Рис. 69. Свободное падение связанной системы: 1 - кабина; 2 - груз; 3 - трос; 4 - направление падения

Невесомость - антипод тяжести. Обычно состояние невесомости мы сочетаем с полетом сверхзвукового самолета либо космической ракеты и связываем его так или иначе с современными достижениями техники. Выражение "Я побывал в состоянии невесомости" обычно приписывается летчикам и космонавтам. Скажите, пожалуйста, а не приходилось ли одному герою известной сатирической книги И. Ильфа и Е. Петрова "Золотой теленок" Самуэлю Паниковскому побывать в состоянии невесомости? Мало того, не ощущали ли вы сами эту самую невесомость, не совершая героических полетов в космос и даже не садясь в самолет? Можно вполне категорично утверждать: да, в состоянии невесомости вы были, и не раз, тысячу раз наблюдали со стороны и еще много раз ощутите и посмотрите, совсем не поднимаясь в небеса.

Вспомните Паниковского.

"Сотрудники вытащили третье глупое дитя лейтенанта Шмидта на крыльцо и принялись неторопливо раскачивать. Паниковский молчал, покорно глядя в синее небо.

- После непродолжительной гражданской панихиды... - начал Остап.

В ту же самую минуту сотрудники, придав телу Паниковского достаточный размах и инерцию, выбросили его на улицу.

- ...тело было предано земле,- закончил Бендер. Паниковский шлепнулся на землю, как жаба". Возьмите в руки камень и, размахнувшись, бросьте его вверх. Описав плавную дугу, камень упадет на землю.

Влезьте, наконец, на вышку и прыгните с нее ласточкой в воду. На худой конец, перескочите с одной ступеньки лестницы на другую.

Вот вам три, казалось бы, совершенно разнородные ситуации. Но в них с точки зрения механики есть нечто общее: свободное падение или свободный полет. Когда Паниковского выбросили на улицу, он совершил некоторый неуправляемый полет, потеряв на мгновение связь с землей; камень и спортсмен, прыгающий с вышки, также свободно падают на землю. И все они в эти краткие промежутки времени находились именно в состоянии невесомости. Она, как видим, не так уж редко встречается в нашей обыденной жизни. Вот поэтому на невесомость не стоит смотреть как на некоторый недосягаемый фетиш, доступный лишь избранным счастливчикам.

В описанном выше примере С. Э. Хайкина показано, что состояние невесомости идеально строго соблюдается для достаточно малых по своим размерам тел. Увеличение размеров тела, несмотря на свободный полет его, приводит к тому, что в нем могут возникнуть внутренние силы, сжимающие или растягивающие его. Остановимся на этом вопросе более подробно.

Вначале рассмотрим модельную задачу, от которой потом перейдем к определению внутренних сил. Предположим, что некоторое тело совершает полет по круговой орбите спутника Земли. Над этим телом на расстоянии рr, совпадающем с направлением радиуса, находится небольшой шарик, масса которого равна m. Какую силу необходимо приложить к шарику, чтобы в процессе движения шарик все время находился над этим телом на одной и той же высоте? Математический анализ показывает, что для поддержания указанного стационарного положения летящих тел необходимо к шарику приложить радиальную силу, направленную к центру Земли. Если шарик расположен ниже летящего предмета на том же расстоянии ρ_r, то величина силы не изменится, а направление ее поменяется на противоположное. Соединив шарики тонкой невесомой нитью, получим равновесную систему, поскольку находящийся вверху шарик будет стремиться оторваться вверх точно с такой же силой, с какой нижний шарик будет стремиться опуститься вниз. При полете на орбите спутника Земли с высотой 200 км, массе шарика 1 кг и длине нити 2 м натяжение нити составит 2,8 - 10^-5 г. Увеличение длины нити или массы шариков приводит к пропорциональному возрастанию силы натяжения нити. Трос, соединяющий два космических корабля, имеющих массы 5 т каждый и расположенных на расстоянии 200 м вдоль радиуса орбиты, будет натянут с силой 14 г.

Пусть теперь на орбиту спутника Земли выведен прямой однородный стержень. В полете он ориентирован так, что продольная ось его 'постоянно направлена к центру Земли. Весь стержень можно мысленно разделить на ряд отдельных шариков, симметрично расположенных относительно середины стержня. Каждая пара таких шариков будет стремиться разделиться и поэтому стержень в целом будет растягиваться. Стальной пруток сечением 1 см и длиной 2 м будет разрываться с силой 10^-4 г. Заметим, что если всю массу прутка поровну рассредоточить на его концах и соединить эти массы нитью, то она окажется натянутой в два раза большей силой. Конечно, найденные значения усилий в стержне или нити сами по себе невелики, например, по сравнению с теми усилиями растяжения, которые может выдержать металлический пруток, но они вполне доступны для непосредственного измерения. Самый простой способ - разрезать нить и между концами ее привязать пружинные весы.

Когда начинается изучение какого-либо нового физического явления, то никто заранее не может предугадать следующих из него выводов и тем более определить применимость его для решения тех или иных вопросов практики. Времена Архимеда и Ньютона безвозвратно минули. Теперь уже трудно открыть новые законы механики путем непосредственного созерцания, скажем, плавающей по воде лодки или падающего с дерева яблока. Мир новых законов закрыт семью замками, охраняется могущественной армией открытых законов и, чтобы взять эту крепость, человечество вынуждено привлечь тяжелую артиллерию в виде ядерных реакторов, циклотронов, лучей лазера, космических ракет, электронных микроскопов, 'быстродействующих вычислительных машин и других китов современной техники, используя в качестве снарядов могучие достижения современной науки. На страницах этой книги мы, конечно, не откроем новых законов, но позволим себе немного пофантазировать, основываясь на некоторых следствиях, вытекающих из закономерностей движения в космосе.

Как вы считаете, можно ли сделать на космическом корабле пилотажно-навигационные приборы, показывающие фактические значения элементов орбиты? Об одном из них - навигационном глобусе мы уже упоминали. Однако он может показать лишь расчетное положение плоскости орбиты в пространстве, ничего не говоря о ее фактическом положении. Основываясь на только что описанном парадоксе - возникновение сил растяжения стержня при свободном полете в космосе,- мы можем изобрести прибор, регистрирующий угловую скорость полета корабля по орбите. Действительно, в формулу, определяющую величину силы растяжения стержня, входит значение угловой скорости полета корабля. Чем выше эта скорость (т. е. чем ниже орбита над Землей), тем эта величина больше. Поскольку сила натяжения стержня прямо пропорциональна угловой скорости, то пружинные весы, предназначенные для измерения силы растяжения стержня, можно отградуировать непосредственно в значениях угловой скорости. В свою очередь при полете по круговым орбитам угловая скорость однозначно определяет период обращения и скорость полета. Значит, наш прибор позволит непосредственно отсчитать по его шкале период обращения и скорость полета. Неплохо? Однако это розовая мечта. Прябор, если его установить на корабле, будет страдать многими "болезнями", он ведь будет измерять буквально все нагрузки, возникающие в стержне, а не только те, которые обусловлены лишь влиянием гравитации. Малейший поворот стержня вместе с кораблем или внутри его приведет к возникновению центробежных сил, которые прибор не сможет отфильтровать. Кроме того, в момент измерений ось стержня должна быть достаточно точно направлена к центру Земли. Любое отклонение от этого направления приведет к уменьшению сил растяжения, т. е. к искажению измеряемых параметров. Все это, разумеется, значительно усложнит эксплуатационные характеристики нашей конструкции и в конечном счете ухудшит точность измеряемых величин.

А нельзя ли этот прибор конструктивно как-то видоизменить, чтобы свести до минимума влияние этих погрешностей?

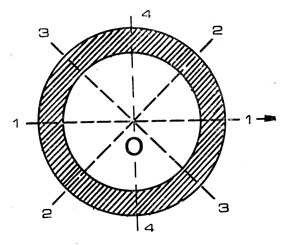
Рис. 70. Кольцо на орбите спутника Земли

Оказывается, можно. Возьмем вместо стержня круглый обод и. совместим его плоскость с плоскостью орбиты корабля (рис. 70). За счет влияния гравитационного поля возникнут силы, стремящиеся разорвать кольцо по сечению" 1 - 1. В любом другом сечении, например, 2 - 2, эти силы будут меньше, чем в сечении 1 - 1, параллельном вектору скорости полета. В сечении 4 - 4 разрывающие усилия будут отсутствовать, т. е. кольцо, разрезанное по этому сечению, само по себе за счет влияния сил притяжения не разорвется. Если кольцо вращается вокруг своей оси О, то за счет влияния центробежных сил в любом его сечении возникнут одни и те же усилия, стремящиеся разорвать его в разные стороны. В то же время усилия во всех сечениях, обусловленные гравитационным полем, несмотря на вращение кольца по отношению к вектору скорости полета, останутся в том же самом положении. Значит, суммарное разрывающее усилие будет слагаться из двух сил: сил, обусловленных влиянием гравитационного поля, и центробежных. Отсюда следует порядок определения величины первой из сил, т. е. угловой скорости полета корабля или его периода обращения: необходимо измерить усилия в сечениях 1 - 1 и 4 - 4, а затем найти их разность. Этим самым исключается влияние вращения нашего прибора на его показания. Но чтобы измерить усилия в сечениях кольца, необходимо знать положение этих сечений относительно вектора скорости корабля. А этого тоже можно избежать следующим нехитрым приемом: нужно измерить усилия в двух взаимно перпендикулярных сечениях и найти их такое положение, когда разность усилий станет наибольшей. Полученная разность усилий пересчитывается далее в угловую скорость полета корабля, период его обращения и.т. д.

Таким образом, применение кольца вместо стержня позволило в принципе избежать влияния собственного вращения на показание прибора, а также исключить операцию ориентации на центр Земли. Однако плоскость кольца в этом случае должна совпадать с плоскостью орбиты полета корабля.

Конечно, видоизменение конструкции прибора не прошла даром, возникли новые проблемы - как измерить возникающие в кольце усилия? Однако это уже другая сторона вопроса и мы позволяем вам решить его по своему усмотрению.

Но в совершающем полет по орбите спутника стержне могут возникнуть не только растягивающие, но и сжимающие усилия. Обратимся вновь к модельной задаче - полету шарика. Если шарик расположить в стороне от плоскости орбиты на расстоянии , то для удержания его в этом положении потребуется приложить горизонтальную силу, перпендикулярную плоскости орбиты. При массе шарика 1 кг и расстоянии ρ_в = 1 м возникает сила, равная 0,1 мг, которая будет стремиться сдвинуть шарик в направлении к плоскости орбиты. Именно за счет влияния этой силы и возникают периодические колебания относительно плоскости орбиты.

В стержне, ось которого ориентирована перпендикулярно плоскости орбиты, также возникнут сжимающие усилия, которые по своей величине в два раза меньше растягивающих.

Конечно, это очень малые усилия. Будущим конструкторам и монтажникам космических кораблей не нужно будет учитывать их влияние на прочность конструкции.

Чтобы покончить с невесомостью, скажем еще несколько слов по поводу условий работы в космосе. В будущем предполагается, что человек будет участвовать в монтаже орбитальных станций, доставляемых € Земли. Стыковка кораблей на орбите спутников Земли - это уже первый шаг на пути создания орбитальных станций. Кому-нибудь наверняка представляется, что работа в космосе не будет тяжелой, потому что в условиях невесомости легко поднять любой груз: ведь само состояние "невесомость" как бы означает "ничего не весит". Значит, человек, работая в космосе, может легко поднять, скажем, груз, равный весу океанского парохода или многоэтажного здания. В действительности дело обстоит иначе.

Оценивая работоспособность человека в космосе, нельзя забывать о физическом свойстве груза, именуемом "инертная масса", и соотношении этих масс между человеком и грузом. "Инертная масса" проявляется как сопротивление тела его перемещению. Тяжелую бетонную плиту, подвешенную на тросах строительного крана, нелегко сдвинуть с места, даже упираясь о землю ногами. Космический монтажник, толкая тяжелый груз и не имея точки опоры, в итоге сам переместится относительно груза, тогда как груз практически останется на месте. Значит, для монтажа орбитальных станций из тяжелых частей, доставляемых с Земли, потребуются ракетные двигатели. Тяжелую физическую работу в условиях невесомости человек соответствующей опоры выполнить не может.