Движение в окрестности точек либрации

Напомним, что такое точки либрации. Как известно, ограниченная задача трех тел рассматривает движение тела пренебрежимо малой массы, в качестве которого можно считать космический аппарат, в гравитационном поле двух конечных точечных масс, которые движутся по круговым орбитам вокруг общего центра масс. С некоторыми приближениями в качестве таких точечных масс подразумевают систему Земля - Луна или Солнце - Юпитер, полагая, что в каждой из этих систем отдельные тела вращаются друг относительно друга по круговым орбитам. Для. этой задачи получены лишь частные (так называемые Лагранжевы) решения. Существо решения состоит в том, что имеются пять точек, обладающих таким свойством, что если космический аппарат помещен в одну из них со строго определенной скоростью, то он будет оставаться в точке, неподвижной относительно вращающихся тел, бесконечно долго. Все точки расположены в плоскости движения конечных масс и их называют точками либрации. Три из них лежат на линии, соединяющей притягивающие центры, а две остальные расположены так, что конечные массы и точки являются неустойчивыми, другие две - устойчивые, если только отношение одной из притягивающих масс к другой меньше - 0,03852. Для системы Земля - Луна отношение масс равно примерно 0,012129, т. е. условие устойчивости треугольных точек либрации выполняется. Это означает, что если космический аппарат расположить вблизи одной из треугольных точек либрации и сообщить ему небольшую относительную скорость, то он будет некоторым образом колебаться относительно этой точки, но никогда не уйдет от нее.

Астрономы установили, что системы Земля - Луна и Солнце - Юпитер удовлетворяют критерию устойчивости движения в окрестностях точек либрации. Примером такого устойчивого движения в природе, как мы уже говорили, является существование астероидов (так называемая Троянская группа) в системе Солнце - Юпитер. Кроме того, известно сообщение К. Кордилевского (Краковская обсерватория) об открытие двух облакообразных скоплений вблизи устойчивых точек либрации системы Земля - Луна.

Предположим, что мы замыслили совершить полет к одной из точек либрации системы Земля - Луна и установить там космическую станцию. Из-за ошибок наведения и управления? космический аппарат никогда точно не выйдет в точку либрации и остановится где-то вблизи ее с небольшой скоростью. Спрашивается, а как будет выглядеть траектория его движения относительно пристани - точки либрации?

Чтобы ответить на этот вопрос, математиками, специалистами небесной механики, были выполнены довольно сложные исследования с использованием методов малых возмущающих ускорений. В результате ими были получены строгие аналитические соотношения, дающие возможность путем несложных вычислений, доступных каждому человеку, определить положение космического аппарата относительно точки либрации, а также установить основные закономерности движения. Вот об этом теперь и пойдет наша речь.

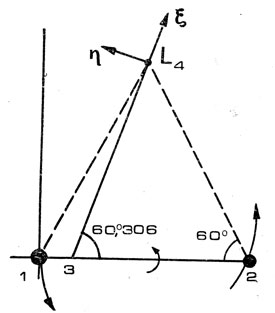
Рис. 71. Устойчивая точка либрации L4 в системе Земля - Луна: 1 - Земля; 2 - Луна; 3 - центр масс системы Земля - Луна

На рис. 71 схематично показано положение Земли, Луны и их орбит движения относительно центра масс. В целях упрощения рисунка центр масс системы Земля - Луна вынесен за границу Земли; фактически он расположен под поверхностью Земли на глубине 1570 км. Одна из устойчивых точек либрации L₄ расположена в плоскости вращения Земли и Луны на равных расстояниях от центров Земли и Луны, т. е. треугольник Земля - точка либрации - Луна является равносторонним и не меняет своих размеров и положения относительно системы тел в процессе их вращения. Симметрично линии Земля - Луна расположена вторая устойчивая точка либрации L₅ (на рисунке она не показана). Проведем теперь прямую из центра масс системы в направлении точки L₄ и ее продолжение от точки L₄ примем за одну из координатных осей, обозначаемой ξ. Вторую координатную ось, обозначенную η, проведем из точки L₄ перпендикулярно оси ξ в направлении вращения системы. Оказывается, что в выбранной таким образом системе координат уравнения движения принимают наиболее простой вид и имеют наглядную геометрическую интерпретацию. Начальные условия движения космического аппарата задаются координатами ξ₀, η₀ и составляющими скорости ξ₀. Когда космический аппарат находится точно в точке либрации и имеет равную с ней скорость, то ξ₀ = η₀ = 0, ξ₀ = η₀ = 0. Значит, заданные в такой системе координат начальные условия движения отражают геометрические характеристики начального возмущения в движении космического аппарата. Чтобы рассчитать траекторию последующего движения космического аппарата при заданных начальных условиях движения, можно воспользоваться формулами, данными в специальных курсах по небесной механике.

В результате анализа уравнений относительного движения можно указать следующие его основные особенности.

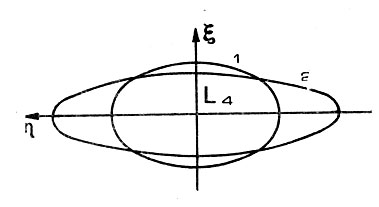
Рис. 72. Разложение возмущенного движения относительно точки либрации Lsub4/sub на два: короткопериодическое (1) и долгопериодическое (2)

1. Движение космического аппарата относительно точки либрации можно трактовать как двоякопериодическое с периодами 28, 62 суток и 91, 71 сутки (при среднем расстоянии между Луной и Землей 384000 км). Иначе говоря, космический аппарат в процессе движения описывает некие периодические траектории, как бы участвуя одновременно в двух колебаниях с различными периодами. Первое из этих колебаний носит название короткопериодического и по величине совпадает с периодом обращения Луны вокруг Земли. Второе из колебаний можно назвать долгопериодическим. По величине период долгопериодических колебаний составляет примерно четвертую часть года. Однако такая зависимость выглядит по крайней мере странно, поскольку при выводе уравнений движения ни Солнце, ни вращение Земли вокруг Солнца не участвовали.

Таблица 6. Размеры полуосей короткопериодической траектории при различных начальных возмущениях

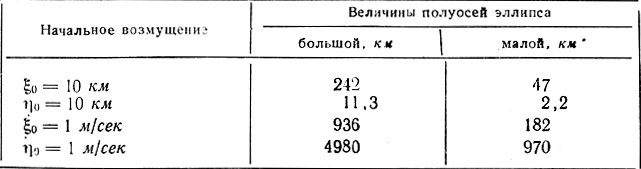
Таблица 7. Размеры полуосей долгопериодической траектории при различных начальных возмущениях

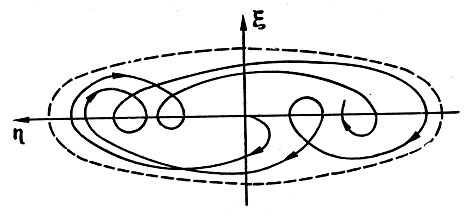
Рис. 73. Одна из траекторий движения относительно точки либрации. Вся она умещается внутри фигуры, напоминающей эллипс

2. Короткопериодические и долгопериодические траектории космического аппарата представляют собой эллипсы (рис. 72). Оси эллипсов совпадают с направлениями осей системы координат ξ, η, а эксцентриситеты их не зависят от величин начального возмущения движения космического аппарата и равны соответственно 0,8709 и 0,9809. Центры эллипсов совпадают с точкой либрации. Размеры эллипсов зависят от начальных условий движения и их численные значения приведены в табл. 6, 7. Таким образом, результирующее движение космического аппарата относительно точки либрации можно представить как сумму движений по каждому из двух эллипсов. Однако всегда можно специально подобрать такие начальные условия, когда космический аппарат будет двигаться по долгопериодической траектории, совершая один виток за 91, 71 сутки или по короткопериодической траектории с периодом 28, 62 суток. В общем же случае, когда на начальные условия движения не наложены какие-либо ограничения, траектория движения космического аппарата не будет представляться замкнутой кривой, а будет состоять из сложным образом чередующихся и неповторяющихся петель. Типичный вид такой траектории показан на рис. 73. Легко заметить, что вся она помещается внутри фигуры, отдаленно напоминающей эллипс и получаемой путем совмещения долгопериодической и короткопериодической траекторий. Границы этой фигуры определяют область возможных движений космического аппарата при данных начальных условиях движения его.

Можно отметить некоторые особенности влияния начальных условий на размеры области допустимых движений. Например, начальное смещение космического аппарата вдоль оси ξ (т. е. в направлении от Земли или к ней) приводит к возрастанию области в несколько десятков раз больше, чем аналогичное смещение по координате η. Иначе говоря, если мы желаем удержать космический аппарат возможно ближе к точке либрации, то в процессе полета к ней необходимо как можно точнее выдерживать расстояние космического аппарата от Земли, нежели его боковое смещение. Далее, отклонение скорости движения космического аппарата относительно скорости точки либрации приводит в некотором смысле к гораздо сильному "разбуханию" области, чем отклонение в координатах. Так, импульс скорости вдоль оси ξ, равный 1 м/сек, эквивалентен начальному отклонению 200 км по координате ξ; импульс скорости вдоль оси ξ, равный также 1 м/сек, эквивалентен отклонению 1500 км по координате η. Эти результаты дают наглядное представление о необходимой точности полета к точке либрации. Следует, наконец, отметить, что если только имеется возможность как-то выбирать начальные условия движения, то их необходимо брать такими, чтобы относительное движение космического аппарата вокруг точки либрации происходило в направлении часовой стрелки. В этом случае размеры области будут значительно меньше, чем при вращении против часовой стрелки.

Чтобы закончить наше повествование о точках либрации, произведем качественную оценку энергетических затрат на достижение устойчивой точки либрации системы Земля - Луна. Примем следующую схему полета. Пусть космический аппарат выведен на круговую орбиту спутника Земли с высотой 220 км и заданным наклонением. В необходимый момент времени включается разгонный двигатель, который переводит космический аппарат на вытянутую эллиптическую орбиту с заданным радиусом апогея r_a. Время включения двигателя должно выбираться из условия, чтобы в процессе полета космический аппарат и точка либрации одновременно пришли в одну и ту же точку пространства. Радиус апогея орбиты, очевидно, должен быть не менее расстояния до точки либрации, т. е. 384000 км, иначе он просто не долетит до нее. По заданной величине радиуса апогея и перигея (последний равен радиусу круговой орбиты) определяется скорость разгона для старта с круговой орбиты. По достижении точки либрации включается корректирующая двигательная установка, которая уравнивает скорость полета космического аппарата до скорости движения точки либрации.

Напомним, что точка либрации, как и Луна, движутся относительно Земли со скоростью примерно 10²⁰м/сек. Однако эта скорость по направлению не совпадает с направлением скорости подлетающего космического аппарата. Результаты расчетов показывают, что для перелета целесообразно использовать орбиты с минимальным апогейным расстоянием. При r_a = 384 000 км, соответствующим минимально вытянутой перелетной орбите, на осуществление разгона с орбиты спутника Земли потребуется скорость 3,126 км/сек. При повышении апогея до 685000 км она увеличится на 40 м/сек. Эти цифры дают наглядное представление об общих энергетических затратах полета к точке либрации. Можно указать, что по суммарному результату они примерно эквивалентны выходу на орбиту спутника Луны по типу полета станции "Луна-10". Конечно, для выбора параметров перелетной орбиты должны быть взяты во внимание вопросы возможности определения орбиты космического аппарата при полете к точке либрации и управления полетом с помощью наземных средств командно-измерительного комплекса.