Скорость полета к Луне

Вопроса о скоростях полета к Луне и, в частности, о минимальной скорости мы уже отчасти касались, когда речь шла о точках либрации системы Земля - Луна. Для первой критической скорости (т. е. наименьшей скорости отлета от Земли, которая в принципе обеспечивает возможность достижения Луны) при старте с орбиты спутника Земли с высотой 200 км, плоскость которой совпадает с плоскостью орбиты движения Луны, было получено значение 10,84890 км/сек. Поскольку скорость полета по такой орбите спутника Земли составляет 7,791 км/сек, то для достижения первой критической скорости потребуется доразгон на величину 3,058 км/сек.

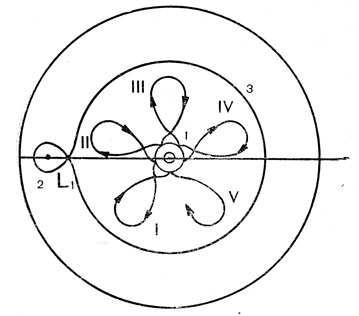
Рис. 76. Первые обороты с минимальной критической начальной скоростью во вращающихся координатах: 1 - Земля; 2 - Луна; 3 - линия Хилла; I, II, III, IV, V - номера витков

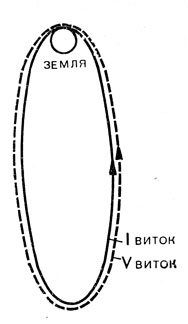
Рис. 77. Предыдущая траектория в невращающейся системе координат

Рассмотрим теперь особенности движения космического аппарата. Проекция траектории полета его при старте с первой критической скоростью во вращающейся вместе с Луной и Землей системой координат на плоскость орбиты Луны показаны на рис. 76. На нем же изображена линия Хилла в виде несимметричной восьмерки, соответствующая указанным условиям старта. Напомним, что линия Хилла определяет границу допустимых движений космического аппарата. Она, в частности, показывает, что достижение Луны может произойти только при пролете космического аппарата через узкую "лазейку", совпадающую с точкой либрации L₁. Расчет траектории полета производился методом численного интегрирования уравнений движения. Результаты расчетов показывают, что при отлете от Земли с первой критической скоростью траектория космического аппарата возвращается к Земле, не доходя до линии Хилла примерно на 30000 км. Орбита космического аппарата на первых витках по форме очень близка к эллипсу с радиусом апогея около 260 тыс. км (рис. 77). Однако от витка к витку высота апогея постепенно возрастает, но темп возрастания ее является очень малым. Для приведенных на рис. 76 пяти оборотов космического аппарата в выбранном масштабе отметить увеличение высоты апогея просто невозможно. Пройдет, следовательно, очень много времени, пока он достигнет линии Хилла. Но это не все: ведь для прилета к Луне необходимо, чтобы космический аппарат достиг линии Хилла в точке L₁, и только после этого он может перейти в левую часть восьмерки, т. е. оказаться в районе Луны. Таким образом, полет к Луне с минимальной скоростью практически оказывается невозможным, поскольку перед его осуществлением космический аппарат должен сделать достаточно большое число оборотов вокруг Земли. Оценочные расчеты, выполненные В. А. Егоровым, показывают, что для достижения линии Хилла космический аппарат должен совершить порядка 200 оборотов, затратив на это 1200 суток. Это объясняется тем, что влияние Луны оказывается относительно небольшим.

Аналогичные расчеты для старта с Земли со второй (10,84968 км/сек), с третьей (10,85738 км/сек) и с четвертой (10,85854 км/сек) критическими скоростями показывают, что здесь также не удается достичь Луны на первом обороте. Следовательно, полет к Луне с такими скоростями также не целесообразен. Вот по, этой причине приходится искать другой подход к задаче выбора скорости полета к Луне.

Мы уже убедились, что на первом обороте движения с минимальными скоростями орбита полета космического аппарата по своей форме очень близка к эллипсу с фокусом в центре Земли и ее можно приближенно (но с хорошей точностью) рассчитывать по эллиптической теории, т. е. без учета притяжения Луны. Это обстоятельство наводит на мысль найти минимальные скорости на первом обороте приближенно, полностью пренебрегая влиянием Луны. Минимальная геоцентрическая начальная скорость, как нетрудно догадаться, должна быть выбрана так, чтобы высота апогея эллипса сравнялась с расстоянием до Луны. При строго вертикальном старте с поверхности Земли эта скорость будет равна 10,90525 км/сек. При старте с орбиты спутника Земли с высотой 200 км она возрастает всего лишь на 1,6 м/сек. Для сравнения укажем, что вторая космическая (параболическая) скорость в этом случае составляет 10,99967 км/сек и, следовательно, минимальная скорость полета к Луне меньше ее всего на 92,828 м/сек. Таким образом, увеличив минимальную скорость полета к Луне всего на 93 м/сек, космический аппарат навсегда покинет Землю и превратится в искусственную планету, вращающуюся вокруг Солнца.

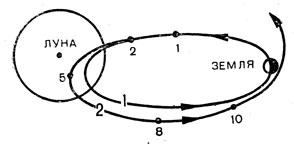
Pис. 78. Возмущение Луной эллипса, достигающего точки равенства притяжений Земли и Луны: 1 - орбита без притяжения Луны; 2 - орбита с притяжением Луны. Точками на орбите обозначено время полета в сутках

Траектория, соответствующая минимальной скорости отлета от Земли, показана на рис. 77. Эти расчеты подтверждают, что выбранное нами условие нахождения минимальной скорости (равенство высоты апогея эллипса расстоянию до Луны) является достаточным для обеспечения попадания в Луну с высокой точностью. Более строгий анализ этого вопроса показывает, что найденную из этого условия скорость полета к Луне необходимо уменьшить на 2 см/сек, что является, конечно, пренебрежимо малой величиной. Полученный результат также означает, что распространенное мнение, будто бы для достижения Луны достаточно достигнуть удаления, на котором притяжения Луны и Земли равны, - неверно. Это подтвердили и расчеты с соответствующих траекторий с учетом притяжения Луны, одна из которых показана на рис. 78. В этом случае за счет влияния притяжения Луны происходит некоторое растяжение начального эллипса и космический аппарат, не достигнув Луны, возвращается к Земле. Любопытно также отметить, что вплоть до момента входа в сферу действия Луны (она на рис. 78 обозначена в виде окружности) фактическая траектория полета очень хорошо совпадает с эллипсом.

Понятно, что величина скорости отлета от Земли целиком определяет продолжительность полета к Луне. Чем больше скорость, тем меньше полетное время. При минимальном значении начальной скорости продолжительность полета составляет немного более четырех суток, при старте с параболической скоростью - около двух суток, а при превышении параболической на 500 м/сек - примерно одни сутки.

Один из наиболее ответственных этапов полета к Луне - это сближение космического аппарата с Луной. Поэтому время полета к Луне выбирают так, чтобы момент сближения был хорошо виден с наземных пунктов управления и наблюдения за полетом. При прямом старте к Луне с территории Советского Союза или старте с первого витка орбиты спутника Земли это требование будет выполнено только в том случае, если продолжительность полета кратна полусуткам, т. е. равна полусуткам, полутора суткам, двум с половиной суткам и т. д. Не случайно поэтому время полета автоматической станции "Луна-2" составляло примерно полутора суток, а в последующих пусках к Луне оно составляло либо 3,5 суток, либо 4,5 суток.