Сближение с Луной

Полет к Луне, как уже сказано, может осуществляться с различными целями. Это - попадание в Луну, переход на орбиту ее спутника или облет с возвращением к Земле. Во всех случаях космический аппарат входит в сферу действия Луны, переподчиняясь, таким образом, влиянию притяжения Луны и уходя навсегда или только временно из-под опеки Земли. Возникает вопрос: а не может ли случиться так, что космический аппарат, войдя в сферу действия Луны, самопроизвольно, без всяких маневров с помощью двигателя, а только под действием притяжения Луны останется около нее, оказавшись вечным пленником Луны? Этот вопрос в небесной механике относят к так называемой проблеме захвата. Применительно к задачам полета к Луне проблема захвата может быть сформулирована так: может ли космический аппарат, стартуя с Земли, на первом витке орбиты полета к Луне быть захвачен Луной, превратившись в ее искусственный спутник? Надо сказать, что этот вопрос в его самой общей постановке является достаточно сложным и некоторые тонкости его еще не разрешены вплоть до настоящего времени. Однако многие стороны его, особенно ценные с практической точки зрения, сейчас выяснены и дают четкий ответ. Об этом, в частности, достаточно подробно говорит советский механик В. А. Егоров в статье "О некоторых задачах динамики полета к Луне" (журнал "Успехи физических наук", т. 62, 1957 г.).

Итак, с точки зрения техники полета очень важно знать, существует ли хоть одна траектория полета к Луне, отвечающая захвату, или нет. Если такая траектория существует, то представляется очень заманчивой идея создания искусственного спутника Луны без помощи двигателя. Конечно, ввиду исключительности начальных условий движения реализовать в точности такую траекторию будет очень трудно, но все же, совершая полет по близкой траектории, желательно хотя бы на некоторое время создать спутник Луны.

Мы уже говорили, что независимо от того, возможен захват или нет, создание временного спутника Луны без помощи двигателя в принципе (теоретически) возможно. Для этого необходимо стартовать от Земли со скоростью, несколько превышающей первую критическую (10,84890 км/сек), но меньше второй (10,84969 км/сек). В этом случае поверхности Хилла, окружающие Землю и Луну, соединяются между собой наподобие гантели и ручка этой гантели образует своеобразную горловину, через которую космический аппарат может проникнуть к Луне. Но для этого он должен сделать достаточно большое число оборотов вокруг Земли. Регулируя скорость отлета от Земли в диапазоне между двумя критическими скоростями (т. е. в интервале 0,78 м/сек), горловину можно сделать очень узкой и поэтому космический аппарат, проникнув через горловину, может двигаться около Луны сколь угодно долго, прежде чем выйдет через нее обратно. Однако практическая реализация такого спутника Луны вряд ли возможна по следующим причинам. Во-первых, отличие первой и второй критической скоростей составляет всего 0,78 м/сек и промежуточную скорость будет очень трудно реализовать технически. Во-вторых, космический аппарат, совершая большое число витков, прежде чем достигнет горловины, может упасть на Землю. В-третьих, неучтенное при этом возмущающее влияние Солнца может либо закрыть горловину, либо, наоборот, расширить ее и увести космический аппарат от Земли и Луны. Таким образом, создание временного спутника Луны без помощи двигателя оказывается фактически невозможным.

А что можно сказать о захвате Луной? Детальный анализ этого вопроса показывает, что ни, при каких начальных условиях отлета космического аппарата от Земли захват его Луной невозможен. Значит, аппарат, стартовавший с Земли и на первом обороте вошедший в сферу действия Луны, обязательно выйдет из нее (разумеется, если только он не столкнется с Луной). Отсюда следует, что создание постоянного спутника Луны на первом обороте без помощи двигателя невозможно.

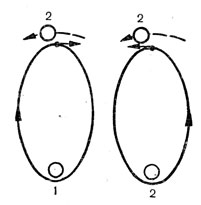
Рис. 79. Орбиты полета к Луне с движением по часовой и против часовой стрелки: 1 - Земля; 2 - Луна

Остановимся теперь более подробно на вопросе входа космического аппарата в сферу действия Луны. Предположим" что аппарат выведен на круговую орбиту спутника Земли высотой 200 км, а плоскость орбиты его совпадает с плоскостью орбиты Луны. Разгоняясь с этой орбиты, можно получать все более и более вытянутые эллипсы" Движение по этим эллипсам может происходить как в направлении часовой стрелки, так и против ее вращения (рис. 79). По мере возрастания высоты апогея скорость полета в этой точке будет убывать. При высоте апогея 100 тыс. км она составит 661 м/сек, при высоте 190 тыс. - 365 м/сек. Когда высота апогея достигнет сферы действия Луны (т. е. апогей не будет доставать Луны на 66 тыс. км), скорость полета уменьшится до 200 м/сек. Наконец, когда апогей коснется орбиты Луны, что соответствует случаю отлета от Земли с минимальной скоростью, скорость полета в апогее станет равной 187 м/сек. Необходимо заметить, что найденные скорости отсчитываются относительно Земли, а не Луны. Чтобы получить скорость космического аппарата относительно Луны, надо учесть собственное движение Луны вокруг Земли, которое происходит со скоростью примерно 10²⁰м/сек. Значит, когда космический аппарат, стартуя с Земли и двигаясь по эллиптической орбите в направлении часовой стрелки, достигнет сферы действия Луны, то его скорость будет направлена навстречу движению Луны и относительно Луны он будет в этот момент лететь со скоростью 1220 м/сек. При полете по орбите против часовой стрелки его относительная скорость уменьшится до 820 м/сек. Теперь вспомним, что параболическая скорость на границе сферы действия Луны составляет всего 383 м/сек. Спутник Луны, имеющий такую скорость, навсегда покинет Луну. Но в лучшем случае при отлете с Земли мы получаем относительную скорость порядка 820 м/сек, которая более чем в два раза превышает вторую космическую скорость Луны. При других ориентациях эллипса подлета к Луне эта скорость еще больше возрастает и достигает максимального значения 1220 м/сек. Отсюда следует интересный вывод: скорость космического аппарата в сфере действия Луны всегда является гиперболической. Вот теперь становится понятным вопрос о том, почему исключается захват аппарата Луной. Гипербола, как мы уже знаем, разомкнутая траектория. Пролетев один раз относительно планеты по гиперболической траектории, космический аппарат больше никогда не вернется к ней.

Нам осталось, наконец, рассмотреть последний вопрос сближения с Луной - вид траекторий космического аппарата относительно Луны при движении внутри сферы ее действия. Обратимся вначале к простому случаю, когда плоскость орбиты полета к Луне и плоскость орбиты Луны совпадают. Старт к Луне производится с минимальной скоростью, когда апогей исходной орбиты касается орбиты Луны. Для уменьшения селеноцентрической скорости движение по орбите полета к Луне производится против вращения часовой стрелки (рис. 80). На рис. 80 точка А соответствует положению космического аппарата в момент пересечения им сферы действия Луны. На участке полета от Земли до точки А движение космического аппарата рассматривалось только под действием притяжения Земли, а начиная с этой точки дальнейшую траекторию необходимо определять с учетом притяжения одной Луны. Если бы Луна была неподвижной, то геоцентрическая скорость аппарата (т. е. скорость его относительно Земли) должна была равняться селеноцентрической скорости (скорости относительно Луны). Но из-за движения Луны относительно Земли, а вместе с нею и сферы действия, космический аппарат после входа в эту сферу как бы скачком изменит свою скорость относительно Луны, что происходит за счет собственного движения Луны вокруг Земли. Для получения селеноцентрической скорости необходимо, следовательно, сложить вектор скорости подлета аппарата к сфере 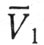с вектором скорости Луны 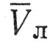, в результате чего определяется вектор скорости 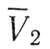полета аппарата относительно Луны (рис. 80). Пользуясь полученным треугольником скоростей, можно удобно и наглядно показать качественный характер полета космического аппарата. Перемещая точку входа А по сфере действия Луны, мы будем тем самым получать различные направления селеноцентрической скорости относительно центра Луны (рис. 81), где точками А₁, ..., А₇ обозначены различные местоположения аппарата в момент достижения сферы действия Луны и селено-центрическая скорость в эти моменты. Теперь рассмотрим различные случаи.

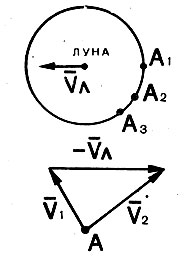
Рис. 80. Треугольник скоростей на входе в сферу действия Луны

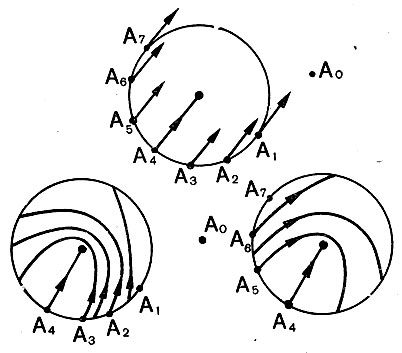
Рис. 81. Траектория движения внутри сферы действия Луны

Случай А₀. При достижении космическим аппаратом точки А₀ - скорость его относительно Луны будет направлена в наружную сторону от сферы действия. Здесь треугольник скоростей вырождается в прямую линию. Действительно, при полете к Луне с минимальной - скоростью точка А0 будет соответствовать апогею подлетной орбиты и скорость полета его в апогее будет параллельна скорости движения Луны. Тогда результирующая скорость, направленная от сферы действия Луны, составит около 820 м/сек. Это означает, что в последующем движении он не войдет в сферу действия Луны и Луна оказывается недостижимой для него. Иными словами, космический аппарат не может входить в сферу действия, догоняя Луну в ее движении по орбите.

Случай А₁. Вектор селеноцентрической скорости касается сферы действия. Космический аппарат достигает сферы действия, но, скользнув по ее поверхности, продолжает полет вокруг Земли. Эта точка является граничной, вход левее ее уже обеспечивает проникновение в сферу действия.

Случай А₂. Вектор скорости направлен внутрь сферы действия. Космический аппарат, проникнув в сферу действия, будет описывать относительно Луны слабоизогнутую (т. е. с большим эксцентриситетом, значительно превышающем единицу) гиперболическую орбиту. Поскольку точки входа и выхода аппарата из сферы действия находятся на одном и том же расстоянии от центра Луны, то космический аппарат после выхода будет иметь по величине ту же самую скорость, что и на входе, но другое направление и поэтому последующий полет относительно Земли изменится. Когда космический аппарат запускался к Луне с минимальной скоростью, то при отсутствии Луны он должен был достигнуть ее орбиты (т. е. точки А₀) и после этого снова вернуться к Земле. Однако после полета в сфере действия Луны он выходит из нее выше точки входа, которая расположена уже дальше от Земли и имеет ту же самую (по величине) геоцентрическую скорость. Это означает, что полная механическая энергия космического аппарата возросла по сравнению с ее значением при полете к Луне. Луна по отношению к прилетевшему к ней космическому аппарату уподобилась своеобразному реактивному двигателю, изменившему последующий полет вокруг Земли. Космический гость с Земли получил подарок от Луны в виде добавки механической энергии. Конечно, точно на такую же величину изменилась механическая энергия движения Луны.

Смещая точку входа еще левее, будем получать все более изогнутые гиперболические орбиты, поскольку они будут все ближе и ближе проходить от центра Луны.

Случай А₄. В этом случае вектор селеноцентрической скорости направлен к центру Луны, т. е. при полете по этой схеме обеспечивается попадание в центр Луны.

Рассматривая общую тенденцию изменения траекторий полета космического аппарата за счет воздействия притяжения Луны при старте с Земли с минимальной скоростью, необходимо отметить, что результирующее влияние Луны сводится к увеличению энергии движения и повороту орбиты внутри сферы действия Луны в направлении против вращения часовой стрелки. Однако, забегая вперед, укажем, что при пусках автоматических станций типа "Зонд-5" или "Зонд-6" облет производился как раз в противоположном направлении, т. е. использовался селеноцентрический эффект, вращающий траектории в направлении часовой стрелки. Это обусловлено тем, что при старте с Земли с минимальной скоростью, оказывается, не существует орбит, позволяющих облететь Луну с поворотом траекторий внутри сферы ее действия против часовой стрелки и вернуться на заданной высоте к Земле. Как же найти выход из создавшегося положения? Выход один - надо увеличить по сравнению с минимальной скорость отлета от Земли. Вот по этой причине высоту апогея орбиты отлета от Земли берут значительно больше расстояния до орбиты Луны. В этом случае для качественного анализа движения допустимо приближение, что при подлете к любой достижимой с Земли точке сферы действия Луны космический аппарат будет иметь одну и ту же геоцентрическую скорость как по величине, так и по направлению. Треугольник скоростей будет иметь одну и ту же форму, независимо от положения точки входа, селеноцентрическая скорость также будет одинаковой во всех точках и начальные участки траекторий будут как бы параллельны между собой (рис. 81).

Точки входа А₁, A₇ являются граничными, в которых космический аппарат может только задеть сферу действия, но не войти в нее. При вхождении аппарата в сферу действия со стороны ее, обращенной к Земле, образуются гиперболические траектории, огибающие Луну как в направлении часовой стрелки, так и навстречу ей.

Разделяющей эти два типа облетных траекторий является точка А₄, через которую осуществляется попадание в центр Луны. Осуществляя вход в сферу действия на участке между точками A₁ и А₄, путем последующего торможения можно создать спутник Луны с левым вращением по орбите, а при входе на участке А₄ - А₇ - с правым вращением. Высота орбиты спутника может регулироваться соответствующим выбором точки входа.

Конечно, в этом простом качественном анализе вопросов полета к Луне мы не в состоянии описать многих тонких эффектов, сопутствующих участку входа и выхода космического аппарата из сферы действия Луны. Мы, например, недостаточно касаемся вопроса о характере орбит полета после выхода из сферы действия Луны. Для этой цели потребовалось бы построение еще одного треугольника скоростей, который уже нельзя будет представить так же просто, как это было выполнено на входе в сферу. Мы также больше ничего не говорим об изменении энергии космического аппарата после облета Луны. Оказывается, в частности, что она может не только возрастать, в чем мы уже убедились, но и убывать. Луна выступает здесь в роли захватчика, отбирающего часть энергии аппарата, увеличивая тем самым собственную энергию. Во всех этих вопросах желающие могут разобраться, обратившись к уже упоминавшейся статье В. А. Егорова.

Теперь скажем несколько слов по поводу пространственного облета Луны. Конечно, динамика движения космического аппарата здесь усложняется еще больше. Влияние Луны скажется в том, что изменению будут подвергаться не только параметры движения, такие, как, скажем, величина скорости полета, но и пространственное положение орбиты. Нам, например, известно, что автоматическая станция "Зонд-6" отлетала от Земли по орбите с наклонением, составляющим примерно 51°,4. Если бы Луна отсутствовала, то станция возвратилась бы к Земле с этим же самым наклонением. Однако влияние Луны привело к тому, что положение плоскости орбиты в пространстве изменилось, и на участке возвращения наклонение составляло примерно 90°. Почему это произошло? Вот примерное качественное объяснение этого явления. Когда станция вошла в сферу действия Луны, то Луна лежала в стороне (справа, если смотреть с Земли) от геоцентрической плоскости орбиты. Боковая сила, возникшая в результате притяжения Луны, стала смещать станцию вбок от первоначальной плоскости движения, как бы стараясь повернуть плоскость орбиты вокруг линии Земля - Луна. Суммарное действие Луны за время, пока станция находилась в ее сфере, и привело к повороту плоскости орбиты так, что наклонение изменилось и приняло значение 90°. Используя этот эффект, можно получать самые неожиданные орбиты и именно это обстоятельство помогло выбрать из них такие, которые позволили осуществить облет Луны и возвратиться на Землю. Однако к этому мы вернемся несколько позже.